储料荷载作用下钢筒仓受力分析与设计

储料荷载作用下钢筒仓受力分析与设计

郑丽华

中冶南方工程技术有限公司结构工程设计所 湖北 武汉 430000

摘 要

钢筒仓结构在矿业、农业、电力、工业等诸多领域中被广泛应用于各种散料的贮存。但我国在钢筒仓结构方面的研究还不够充分，规范计算尚不全面，近些年也有筒仓事故发生。因此，对钢筒仓的规范计算方法的合理性进行进一步的探讨和研究具有理论意义和工程价值。

本文以实际工程为例，采用规范方法和有限元方法对2种储料钢筒仓进行受力分析和设计。首先介绍了规范中的设计计算方法，然后采用该方法对实际工程中的2种储料钢筒仓进行加载计算，得出受力的最不利位置；接着利用ANSYS有限元软件中的壳单元模拟建立钢筒仓三维模型，分析储料荷载作用下筒仓的受力行为；最后，通过比较规范方法和有限元方法的计算结果，列出两种计算结果的差异，分析产生差异的原因，并提出相应的解决办法，为钢筒仓结构的工程设计提供参考。

关键词：储料荷载；钢筒仓；受力行为；简化计算方法；有限元分析

本文的研究对象是钢筒仓。

本课题研究背景及意义

钢筒仓是由壁板和加劲肋共同作用的一种组合薄壳结构，因自身结构性能复杂从而导致钢筒仓在实际应用中面临许多难题。由于我国还没有关于钢筒仓专门的设计规范来指导设计，只有一些相关的书籍介绍了钢筒仓的简化计算方法，这些方法中包含有大量的参数和冗长的计算公式，使得其计算需要耗费大量的时间且不能保证其结果的完全正确性。所以本文以工程实例为研究对象，先用规范方法计算钢筒仓受力结果，然后应用有限元方法进行计算，通过对比分析二者的结果差异及产生差异的原因，可以找出规范计算方法的不足之处以及有限元方法的可取之处，通过综合应用两种方法可以使今后的钢筒仓计算更安全，更合理。

本文的主要工作

本课题的研究目标是在已知筒仓中物料的物理特征参数的条件下，对2个储料钢筒仓分别用规范方法及有限元方法进行受力分析。由于钢筒仓的分类很多，其受力特性也不相同，所以本文只针对矩形筒仓的漏斗仓进行分析，研究内容包括：

1. 采用规范方法对工程实例进行计算分析，求出漏斗壁板及加劲肋的应力及挠度。

2. 采用ANSYS有限元软件建立工程实例的分析模型，得出漏斗壁板及加劲肋的应力和挠度。

3. 比较规范方法和有限元方法的计算结果，得出两种方法计算结果的不同之处，分析产生结果差异的原因，提出相应的解决办法，供设计人员参考使用。

基于规范方法的钢筒仓分析设计

钢筒仓的计算分析

钢筒仓的分类

筒仓结构类型分为深仓和浅仓：当筒仓内贮料计算高度与圆形筒仓内径或与矩形筒仓短边之比大于或等于1.5时为深仓，小于1.5时为浅仓。深仓需考虑直段的摩擦力、漏斗的法向力、摩擦力不随高度改变；浅仓不考虑直段的摩擦力、漏斗的法向力、摩擦力随高度改变。贮料物理参数应通过试验分析或根据实践经验确定，并由工艺设计专业提供。

钢筒仓的荷载

作用在筒仓上的荷载分为：永久荷载、可变荷载和地震作用。其中：

1. 永久荷载：结构自重、其他构件及固定设备施加在仓上的作用力、预应力、土压力、填料及环境温度作用等；

2. 可变荷载：贮料荷载、雪荷载、风荷载、可移动设备荷载、固定设备中的活荷载及设备安装荷载、积灰荷载、筒仓外部地面的堆料荷载及管道输送产生的正、负压力等；

3. 地震荷载：本次研究的可变荷载主要为贮料压力，散料的压力是由筒仓结构类型和贮料的物理特性决定的。

矩形筒仓的受力特点

根据筒仓结构布置的不同，筒仓结构构件的受力状态不尽相同：

1. 布置水平加劲肋的钢筒仓，水平加劲肋既要承受壁板传来的法向压力引起的弯矩，也要承受相邻斜壁传来的水平拉力；壁板承受竖向荷载引起的全部斜向拉力，在法向压力作用下单向或双向受弯。

2. 布置双向交叉加劲肋的钢筒仓，可按主次梁体系计算壁板和垂直加劲肋的弯矩。壁板双向受弯并承受斜向拉力；垂直加劲肋仅承受壁板传来的法向荷载引起的弯矩；水平加劲肋既要承受壁板和垂直加劲肋传来的法向荷载引起的弯矩，也要承受相邻侧壁传来的水平拉力。

钢筒仓的工程实例计算

某高炉矿焦槽中使用了粉矿仓、焦丁仓2个矩形钢筒仓，粉矿仓为低壁浅仓；焦丁仓为深仓；本章以这2个形状规则，下料口偏心尺寸均为0且内置物料重度相近的筒仓为研究对象，通过使用规范的计算方法对其进行计算和设计，最后得出满足这2个钢筒仓受力及变形要求的壁厚及加劲肋构件的大小。

表2.1 2个钢筒仓基本数据表

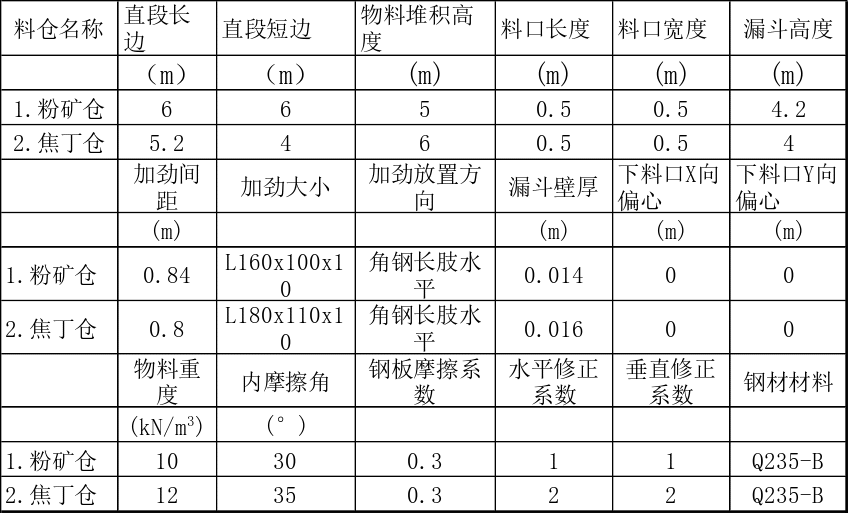
说明：Q235-B，钢材设计强度f=215 MPa，钢材弹性模量E= 206000MPa

粉矿仓

1. 设计数据

1. 1. 贮料种类：无烟煤

   2. 贮料物理特性：

重力密度：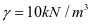

内摩擦角：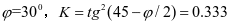

1. 3. 工作条件：

结构重要性系数： ；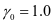

贮料冲击影响系数： ；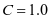

贮料顶面为水平面，贮料装至仓顶。

1. 4. 钢仓材料：

钢仓采用Q235，焊条E43型；

钢材设计强度 f=215 MPa；

钢材弹性模量 E=206000MPa；

2. 钢仓几何特性

   1. 仓的容积

上部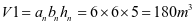

下部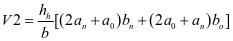

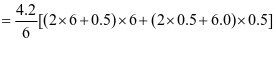
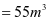
1. 2. 斜壁斜高及斜壁与水平面夹角

斜高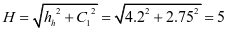

倾角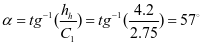

1. 3. 相邻斜壁交肋与水平面夹角

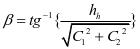
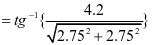
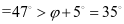
图2‑1 钢仓几何尺寸示意图之一

3. 结构布置与荷载计算

1. 结构布置，本例中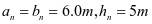 ,根据钢仓结构布置原则，本例采用一肢水平放置的角钢加劲肋并在底部附加一道钢板垂直加劲肋。水平加劲肋间距直壁为5/4=1.25m，斜壁段为4.2/5=0.84m。

2. 贮料压力计算，本例 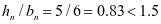，属于低壁浅仓。

仓壁水平压力修正系数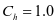 ；钢漏斗竖向压力修正系数 。

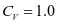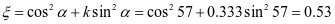
斜壁法向压力标准值：

斜壁顶部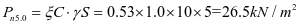

斜壁底部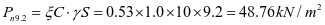

中间各段法向压力标准值见图2-8及图2-9。

图2‑2 筒仓加劲肋布置图

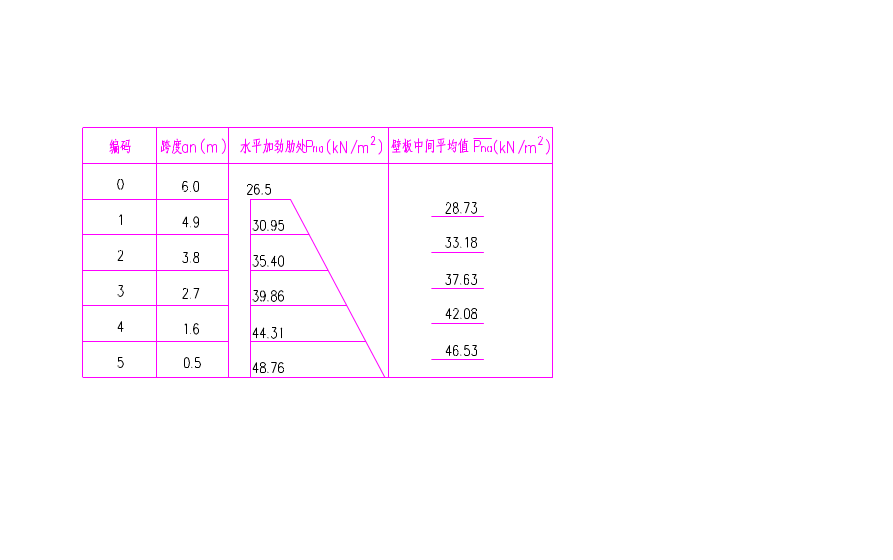
图2‑3 斜壁法向压力标准值

3. 钢仓自重计算，自重荷载标准值近似按下式估算

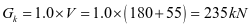
此处不考虑内衬和卸料口给料设备自重。

4. 钢仓内力计算

1. 斜壁斜向拉力设计值

斜壁顶部

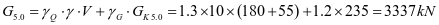
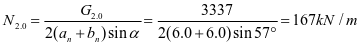
斜壁底板

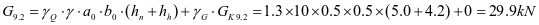
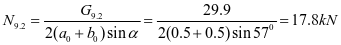
2. 斜壁弯矩设计值

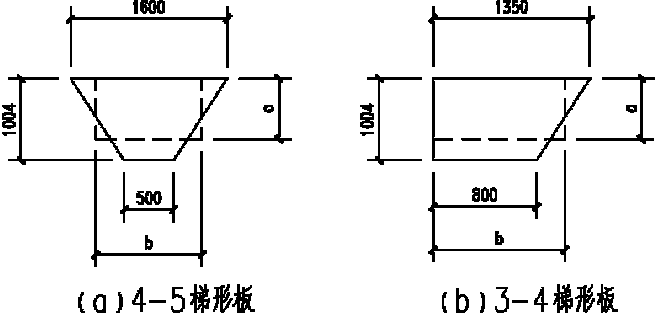
图2‑4 梯形板尺寸

4-5梯形板（图2-10a）

将其折算为矩形板

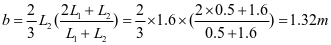
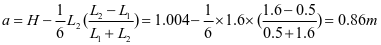
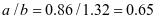,查表2-1得

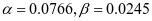
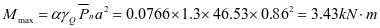
3-4梯形板（图2-10b）

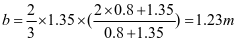
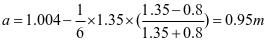
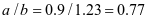,查表2-1得

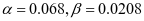
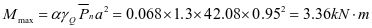
2-3单向板

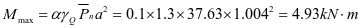
1-2单向板

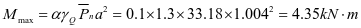
1-0单向板

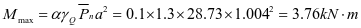
3. 水平加劲肋内力计算

①1号加劲肋框架

加劲肋承受水平荷载标准值：

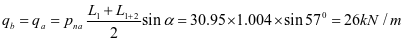
加劲肋水平拉力设计值：

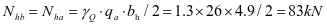
加劲肋弯矩设计值：

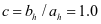
支座：

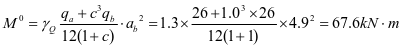
跨中：

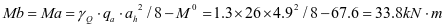
②2号加劲肋框架

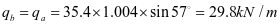
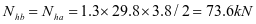
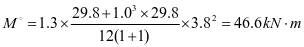
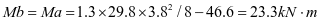
③3号加劲肋框架

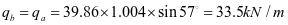
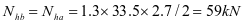
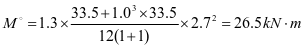
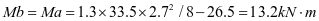
④4号加劲肋框架

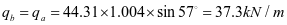
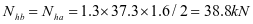
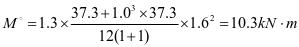
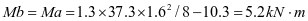
4. 垂直加劲肋弯矩设计值

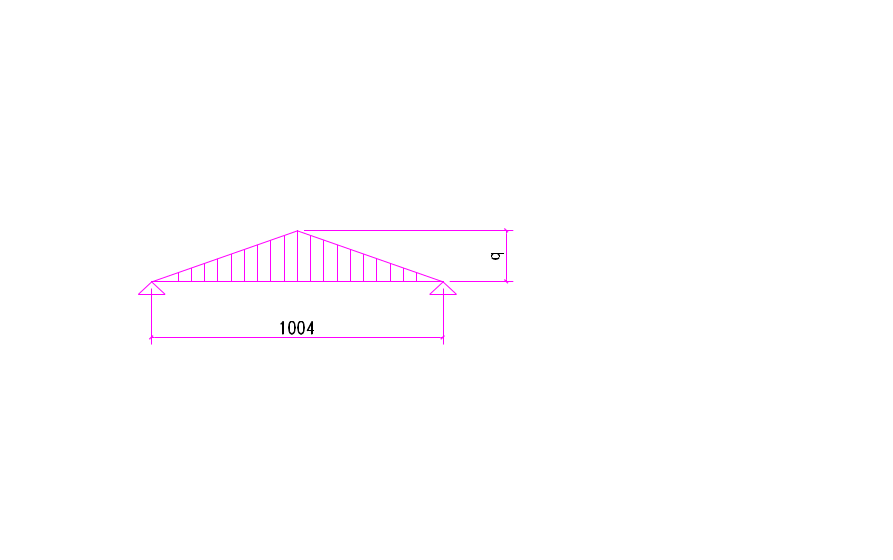
图2‑5 垂直加劲肋计算简图

3~4号水平加劲肋间的垂直加劲肋承受如图2-11所示荷载，其荷载标准值近似取

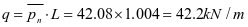
跨中弯矩设计值

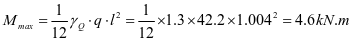
5. 钢仓构件设计

1. 1. 1. 1. 斜壁壁板

①壁板强度，壁板两组最大内力设计值如下

4-5板：Mmax=3.43kN.m,N=17.8kN

0-1板：M=3.76kN.m,Nmax=167kN

根据最大弯矩初选截面

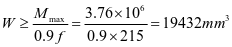
板厚

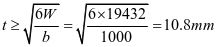取t=14mm

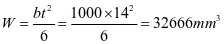
斜壁强度

4-5板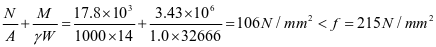

0-1板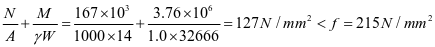

②壁板刚度，斜壁壁板最大挠度在2-3板跨中

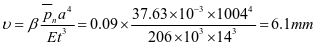
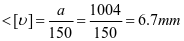
1. 1. 1. 2. 水平加劲肋

①水平加劲肋强度，1号加劲肋框架内力设计值如下

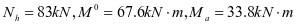
根据最大弯矩初选截面

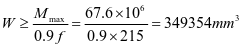
选用L160x100x10，角钢与壁板组成的组合截面1，其截面特性如下：

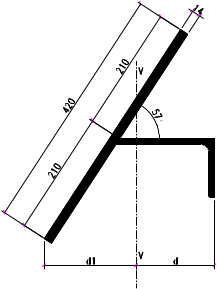
图2‑6 组合截面1尺寸示意图

,

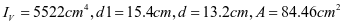
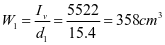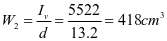
加劲肋强度

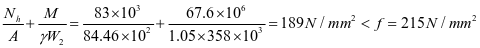
②水平加劲肋刚度，对1号水平加劲肋

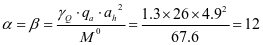
查表2.2得出，ξ=1.0

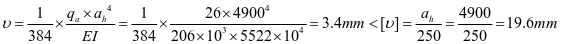
③水平加劲肋强度，2号加劲肋框架内力设计值如下：

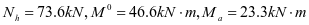
根据最大弯矩初选截面

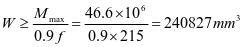
选用L160x100x10，角钢与壁板组成的组合截面1，其截面特性如下：(图2-12)

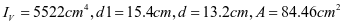
加劲肋强度

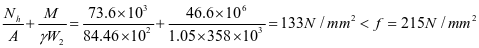
④水平加劲肋刚度，对2号水平加劲肋

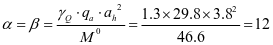
查表2.2得出，ξ=1.0

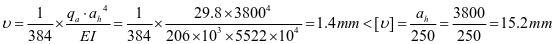
⑤水平加劲肋强度，3号加劲肋框架内力设计值如下：

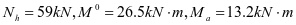
根据最大弯矩初选截面

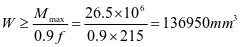
选用L160x100x10，角钢与壁板组成的组合截面1，其截面特性如下：(图2-12)

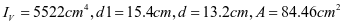
加劲肋强度

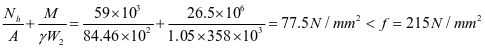
⑥水平加劲肋刚度，对3号水平加劲肋

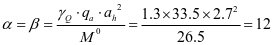
查表2.2得出，ξ=1.0

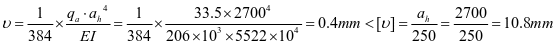
⑦水平加劲肋强度，4号加劲肋框架内力设计值如下：

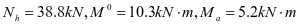
根据最大弯矩初选截面

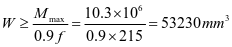
选用L160x100x10，角钢与壁板组成的组合截面1，其截面特性如下：(图2-12)

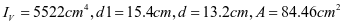
加劲肋强度

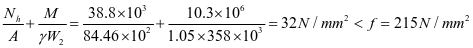
⑧水平加劲肋刚度，对4号水平加劲肋

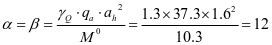
查表2.2得出，ξ=1.0

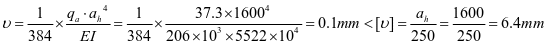
1. 1. 1. 3. 垂直加劲肋

①垂直加劲肋强度，弯矩设计值为M=4.6kN.m

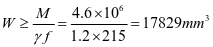
选用钢板加劲肋-80x8(图2-13)

图2‑7 垂直加劲肋尺寸示意图

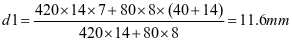
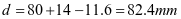
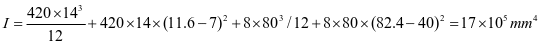
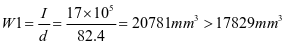
②垂直加劲肋刚度

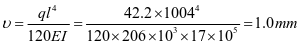
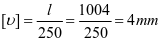
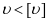，计算满足。

6. 结果：本例中钢漏斗壁厚为14mm,水平加劲肋采用不等边角钢L160x100x10水平放置，垂直加劲肋采用钢板-80x8。

焦丁仓

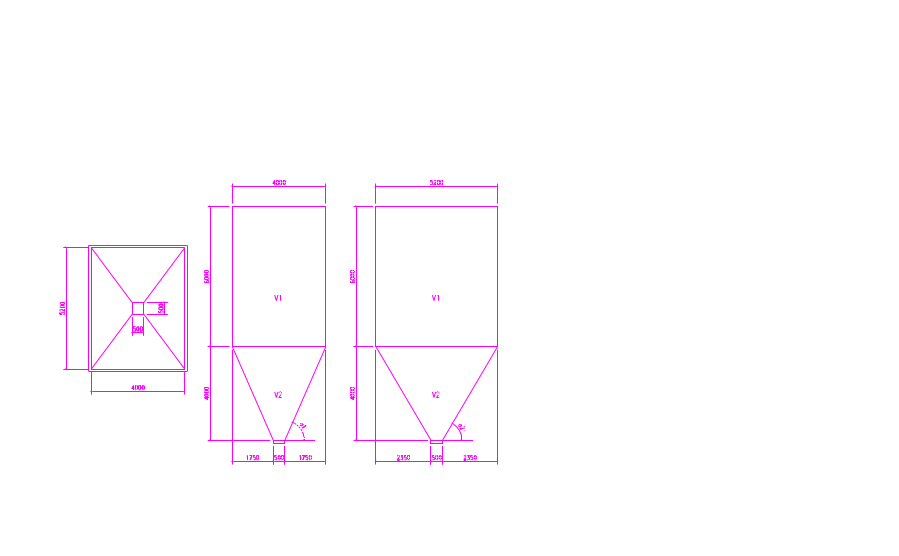
图2‑8 钢仓几何尺寸示意图之一

1. 设计数据

   1. 贮料种类：焦丁煤

   2. 贮料物理特性：

重力密度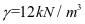

内摩擦角：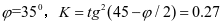

1. 3. 工作条件：

结构重要性系数： ；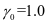

贮料冲击影响系数 ；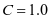

贮料顶面为水平面，贮料装至仓顶。

1. 4. 钢仓材料：

钢仓采用Q235，焊条E43型。

钢材设计强度 f=215 MPa ；

钢材弹性模量 E=206000 MPa ；

2. 钢仓几何特性

1. 仓的容积

上部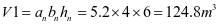

下部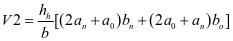

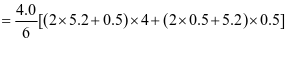
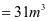
2. 斜壁斜高及斜壁与水平面夹角

斜高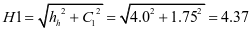

倾角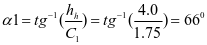

斜高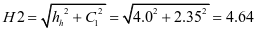

倾角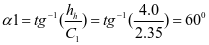

3. 相邻斜壁交肋与水平面夹角

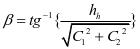
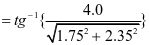
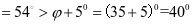
3. 结构布置与荷载计算

1. 结构布置，本例中an=5.2m,bn=4.0m,hn=6m,根据钢仓结构布置原则，本例采用一肢水平放置的角钢加劲肋并在底部附加一道钢板垂直加劲肋。水平加劲肋间距斜壁段为4/5=0.8m。

2. 贮料压力计算，本例hn/bn=6/4=1.5,属于深仓。

仓壁水平压力修正系数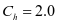 ；钢漏斗竖向压力修正系数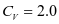

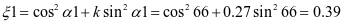
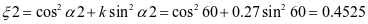
斜壁上法向压力标准值是一个恒定的值：

斜壁顶部

_{；；；；；}

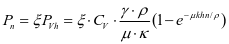
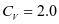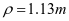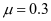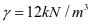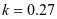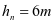
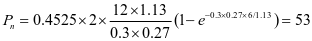
中间各段法向压力标准值见图2-22及图2-23

3. 钢仓自重计算，自重荷载标准值近似按下式估算

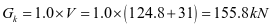
此处不考虑内衬和卸料口给料设备自重。

图2‑9 筒仓加劲肋布置图

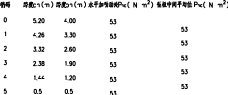
图2‑10 斜壁法向压力标准值

4. 钢仓内力计算

1. 斜壁斜向拉力设计值

斜壁顶部

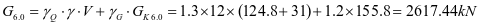
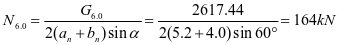
斜壁底板

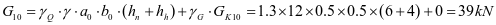
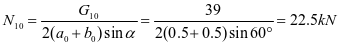
2. 斜壁弯矩设计值

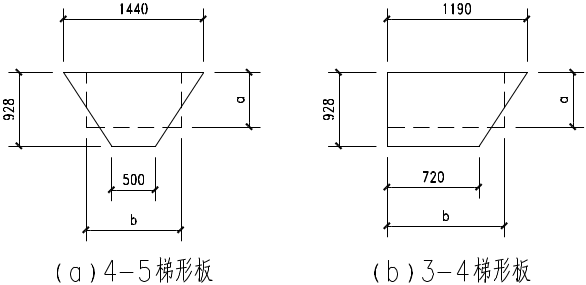
图2‑11 梯形板尺寸

4-5梯形板（图2-24a）

将其折算为矩形板

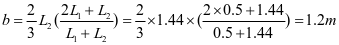
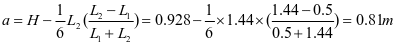
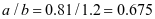,查表2-1得

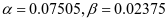
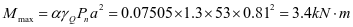
3-4梯形板（图2-24b）

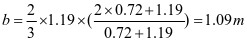
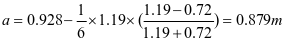
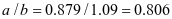,查表2-1得

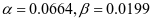
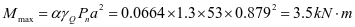
2-3单向板

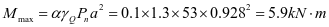
1-2单向板

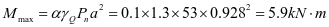
1-0单向板

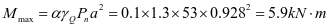
3. 水平加劲肋内力计算

1. 1号加劲肋框架

加劲肋承受水平荷载标准值：

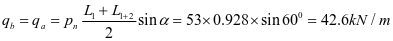
加劲肋水平拉力设计值：

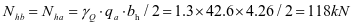
加劲肋弯矩设计值：

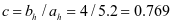
支座：

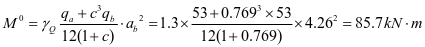
跨中：

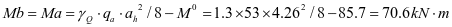
②2号加劲肋框架

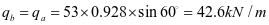
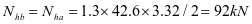
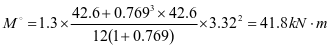
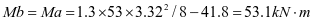
③3号加劲肋框架

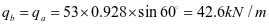
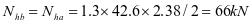
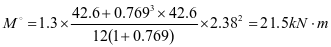
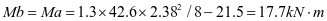
④4号加劲肋框架

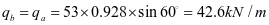
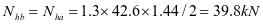
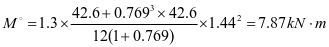
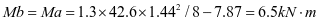
4. 垂直加劲肋弯矩设计值

图2‑12 垂直加劲肋计算简图

3~4号水平加劲肋间的垂直加劲肋承受如图2-26所示荷载，其荷载标准值近似取

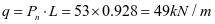
跨中弯矩设计值

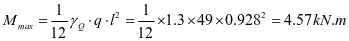
5. 钢仓构件设计

5. 1. 1. 斜壁壁板

①壁板强度，壁板两组最大内力设计值如下

4-5板：Mmax=3.4kN.m,N=22.5kN

0-1板：M=5.9kN.m,Nmax=164kN

根据最大弯矩初选截面

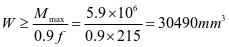
板厚

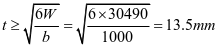取t=16mm

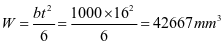
斜壁强度

4-5板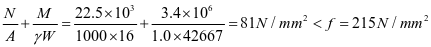

0-1板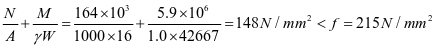

②壁板刚度，斜壁壁板最大挠度在2-3板跨中

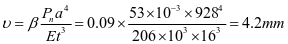
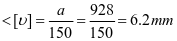
5. 1. 2. 水平加劲肋

①水平加劲肋强度，1号加劲肋框架内力设计值如下

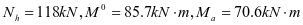
根据最大弯矩初选截面

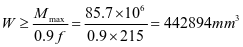
选用L180x110x10，角钢与壁板组成的组合截面1，其截面特性如下：

,

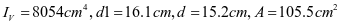
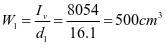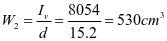
加劲肋强度

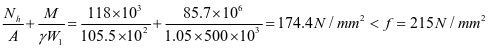
②水平加劲肋刚度，对1号水平加劲肋

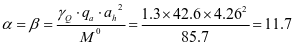
查表2.2得出，ξ=0.892

③水平加劲肋强度，2号加劲肋框架内力设计值如下：

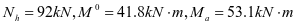
根据最大弯矩初选截面

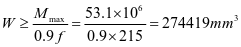
选用L180x110x10，角钢与壁板组成的组合截面1，其截面特性如下：(图2-26)

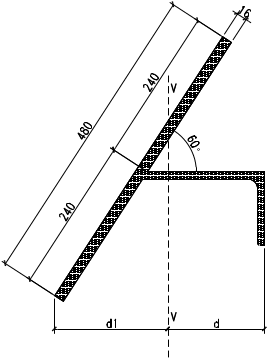
图2‑13 组合截面1尺寸示意图

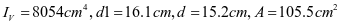
加劲肋强度

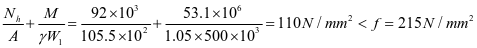
④水平加劲肋刚度，对2号水平加劲肋

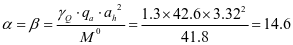
查贮仓结构手册表4.14得出，ξ=1.708

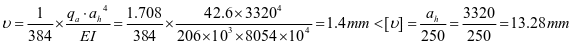
⑤水平加劲肋强度，3号加劲肋框架内力设计值如下：

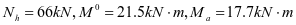
根据最大弯矩初选截面

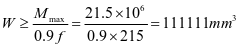
选用L180x110x10，角钢与壁板组成的组合截面1，其截面特性如下：(图2-13)

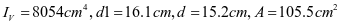
加劲肋强度

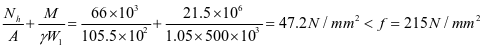
⑥水平加劲肋刚度，对3号水平加劲肋

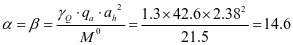
查表2.2得出，ξ=1.708

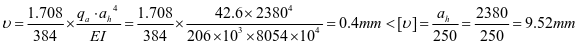
⑦水平加劲肋强度，4号加劲肋框架内力设计值如下：

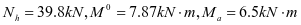
根据最大弯矩初选截面

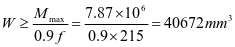
选用L180x110x10，角钢与壁板组成的组合截面1，其截面特性如下：(图2-13)

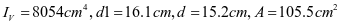
加劲肋强度

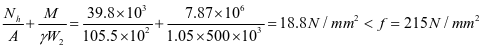
⑧水平加劲肋刚度，对4号水平加劲肋

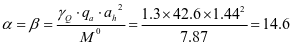
查表2.2得出，ξ=1.708

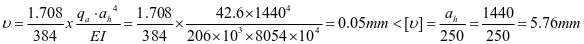
5. 1. 3. 垂直加劲肋

①垂直加劲肋强度，弯矩设计值为M=4.57kN.m

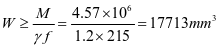
选用钢板加劲肋-80x8(图2-14)

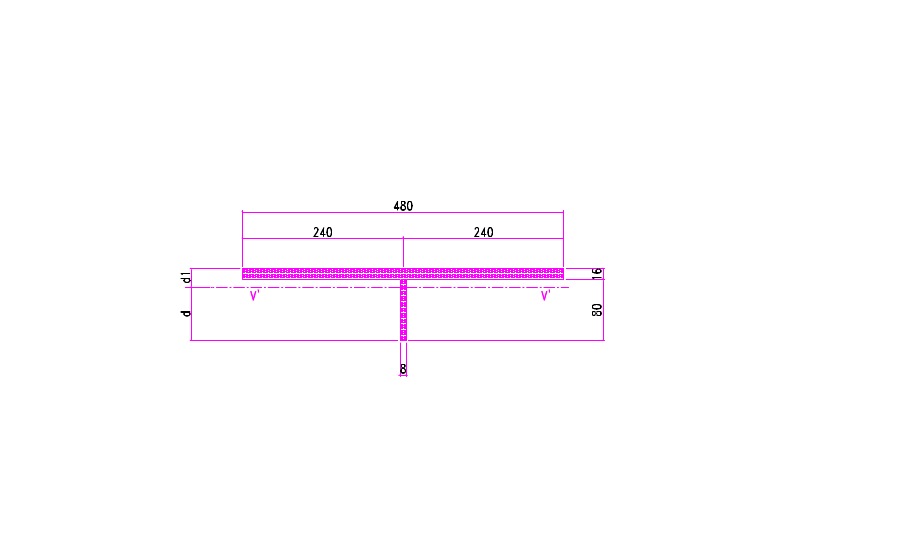
图2‑14 垂直加劲肋尺寸示意图

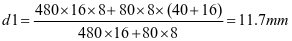
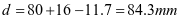
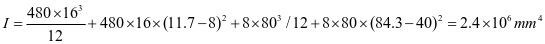
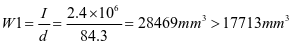
②垂直加劲肋刚度

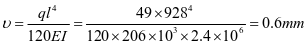
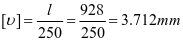
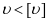，计算满足。

6. 结果：本例中斜壁板选用钢板t=16,水平加劲肋采用不等边角钢L180x110x10,垂直加劲肋采用钢板-80x8。

本章小结

本章首先介绍了规范方法对钢筒仓结构的分类以及筒仓荷载的分类，然后归纳出矩形筒仓的受力特点以及浅仓、深仓两种结构的计算公式，最后应用规范方法分别对粉矿仓、焦丁仓2个矩形钢筒仓进行受力分析，得出以下结论：

1. 规范方法将筒仓结构划分为浅仓及深仓两大类，两种结构内力的计算公式不同。

2. 筒仓的荷载分为三大类：永久荷载、可变荷载、地震。

3. 2种矩形钢筒仓的计算结果如下：

1. 粉矿仓为6x6x4.2(长x宽x高)低壁浅仓，内部物料重度为10kN/m³。钢筒仓壁厚为14mm,水平加劲肋采用不等边角钢L160x100x10水平放置,垂直加劲肋采用钢板-80x8。

2. 焦丁仓为5.2x4x4(长x宽x高)深仓，内部物料重度为12kN/m³。钢筒仓壁厚为16mm,水平加劲肋采用不等边角钢L180x110x10水平放置,垂直加劲肋采用钢板-80x8。

钢筒仓受力行为的有限元分析

随着科学技术的发展，有限元法被广泛应用于土木工程及其他许多工程领域。有限元法不仅适用于静力分析，而且适用于动力分析；它研究对象广泛，不仅可解决杆系结构分析问题，而且能进行平面、空间连续体、板壳及各种复杂组合结构的计算；不仅可分析结构的弹性性能，还能应用于弹塑性等其他复杂力学性能问题的解答。

在上节中，本文阐述了规范对筒仓各个构件的求解是将各构件假设为平面的梁、板结构，较少考虑各构件间的共同受力作用，而实际上筒仓是由仓壁、漏斗壁及边梁整体连接，即是由薄板、构件组合为一个整体的空间结构，在贮料荷载作用下，各相邻构件通过变形协调而共同受力，因而各构件需考虑相邻构件对其变形的约束而引起的内力变化。应用有限元分析方法对筒仓进行受力分析时可以避免这一问题的发生，本节应用ANSYS软件对上节中的工程实例进行有限元分析并得出结果。

钢筒仓受力行为的ANSYS分析

分析模型

采用ANSYS有限元软件中的Shell181单元模拟钢筒仓壁板，beam188单元模拟加劲肋。建模完成后进行网格划分，采用四边形单元，网格尺寸约为0.6m,筒仓荷载均转化为节点力，最后采用小变形静力求解器进行分析。

2种钢筒仓的基本数据与规范方法中的相同，现列表如下：

表3.1 2个钢筒仓基本数据表

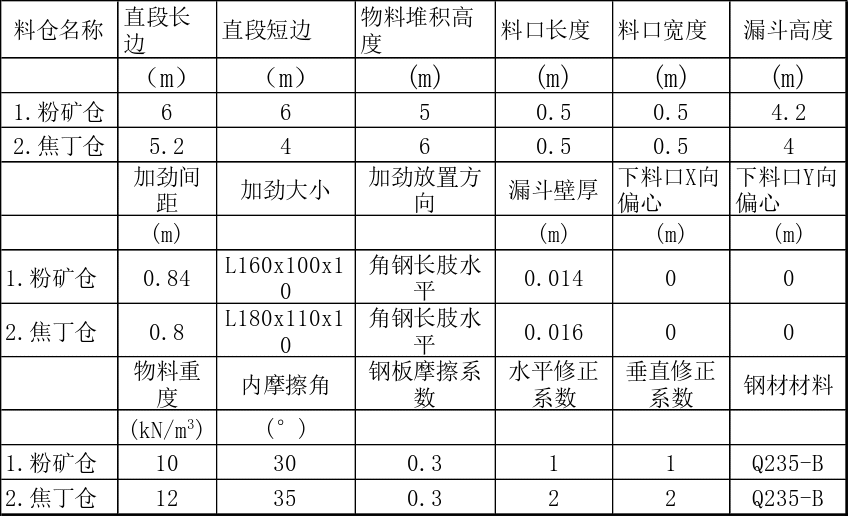
说明：Q235-B，钢材设计强度f=215 MPa，钢材弹性模量E= 206000MPa

粉矿仓

ANSYS计算结果如下：

1. 1. 漏斗顶部壁板最大应力设计值：141.4MPa;漏斗底部壁板的应力设计值：44.1 MPa。

   2. 漏斗壁板的中上部挠度最大，数值为：9.53mm。

   3. 漏斗顶部第2根加劲肋的最大应力设计值：295.4 MPa。

   4. 漏斗顶部第二根加劲肋的变形最大，数值为：8.386 mm。

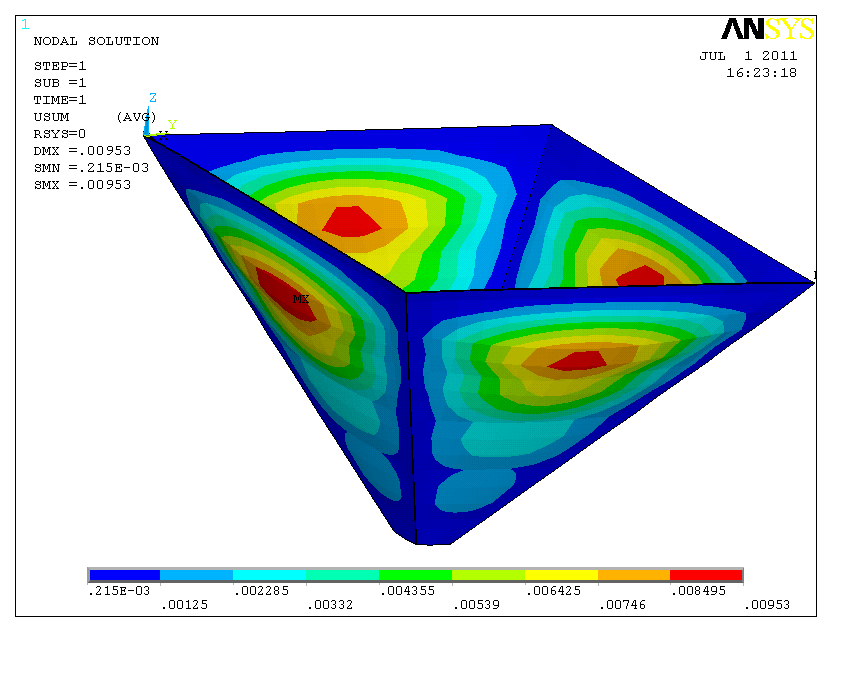
图0‑1 漏斗壁板的位移图

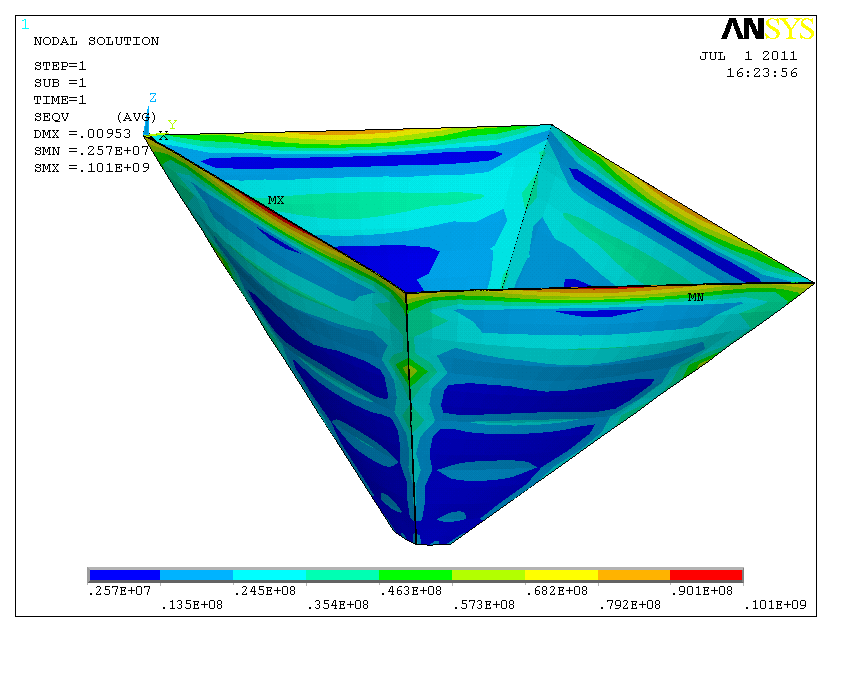
图0‑2 漏斗壁板的应力图

图0‑3 漏斗加劲肋的位移图

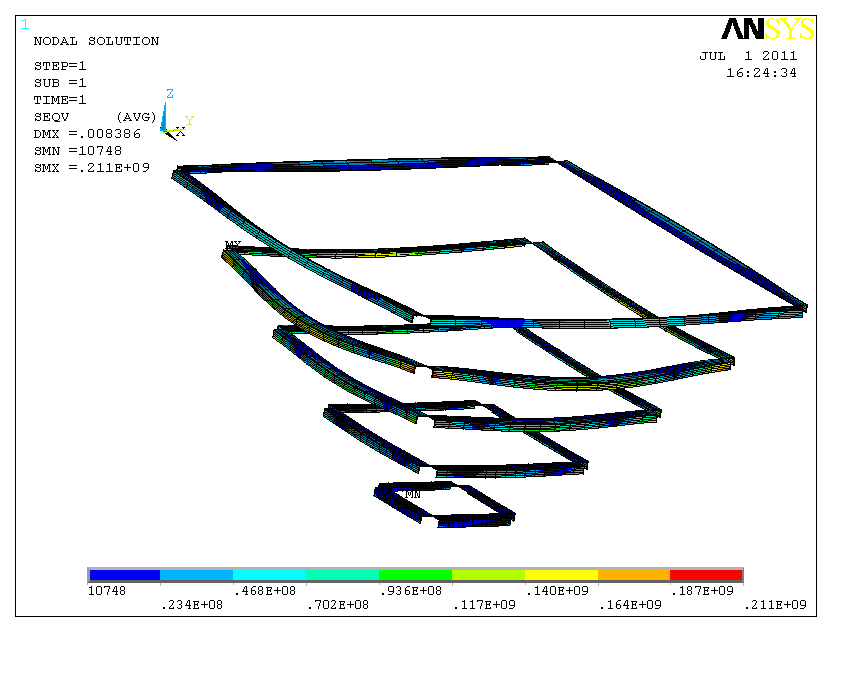
图0‑4 漏斗加劲肋的应力图

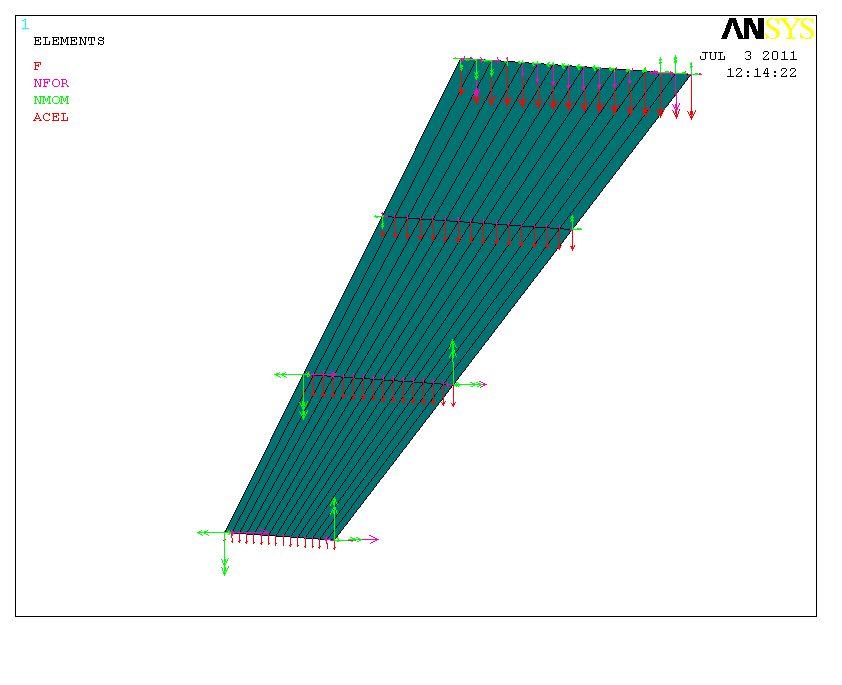
图0‑5 漏斗底部壁板的荷载图

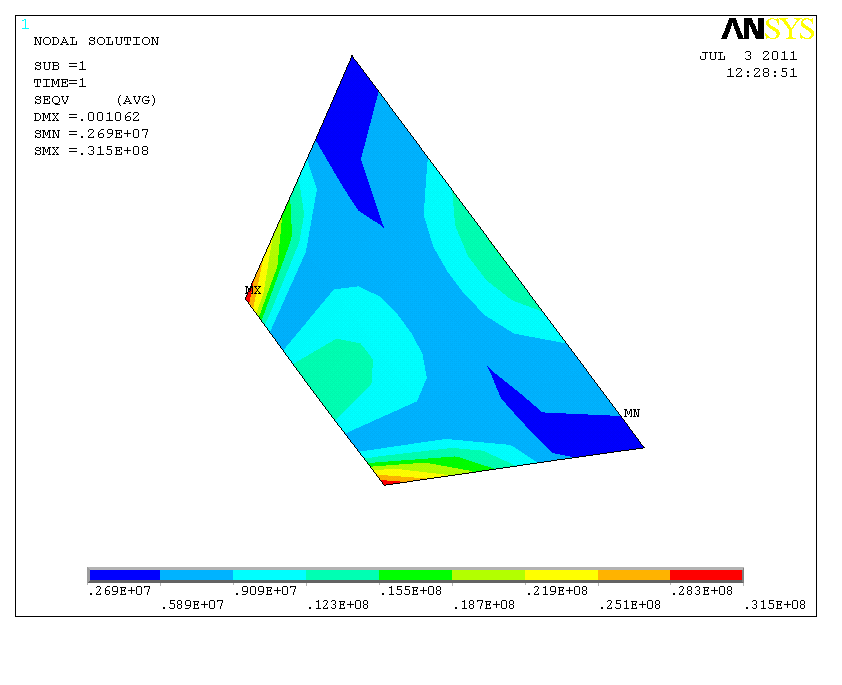
图0‑6 漏斗底部壁板的应力图

图0‑7 漏斗底部加劲肋的应力图

焦丁仓

ANSYS计算结果如下：

1. 漏斗顶部壁板最大应力设计值：188MPa；漏斗底部壁板的应力设计值：34.16 MPa。

2. 漏斗壁板的中上部挠度最大，数值为：6.53mm。

3. 漏斗顶部第2根加劲肋的最大应力设计值：246.4MPa。

4. 漏斗顶部第二根加劲肋的变形最大，数值为：5.813 mm。

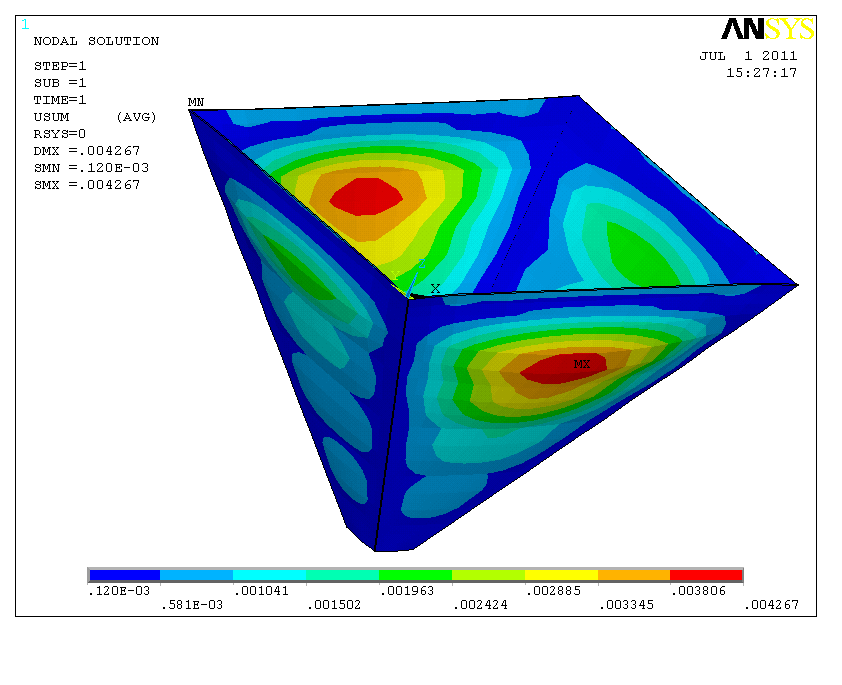
图0‑8 漏斗壁板的位移图

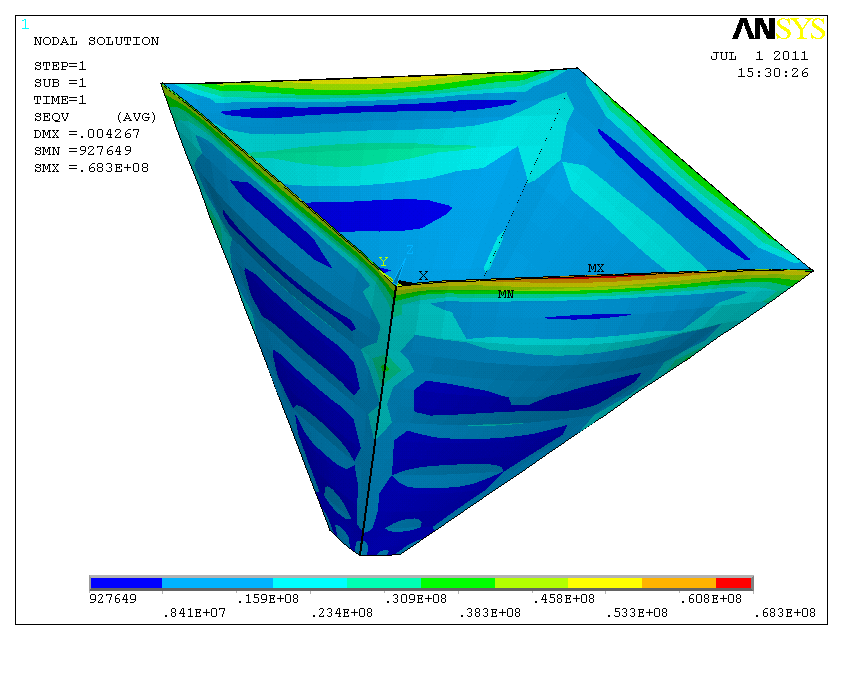
图0‑9 漏斗壁板的应力图

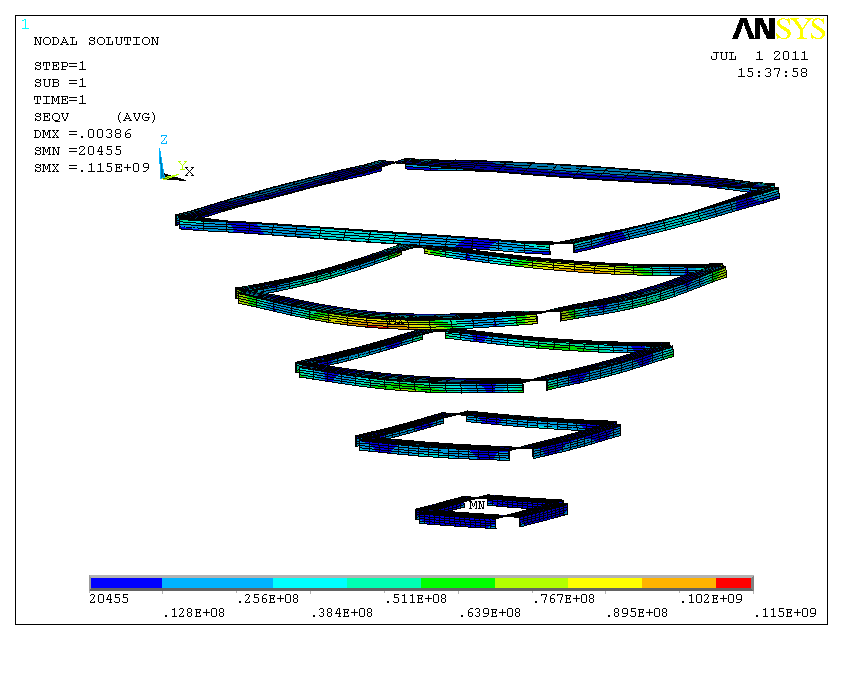
图0‑10 漏斗加劲肋的应力图

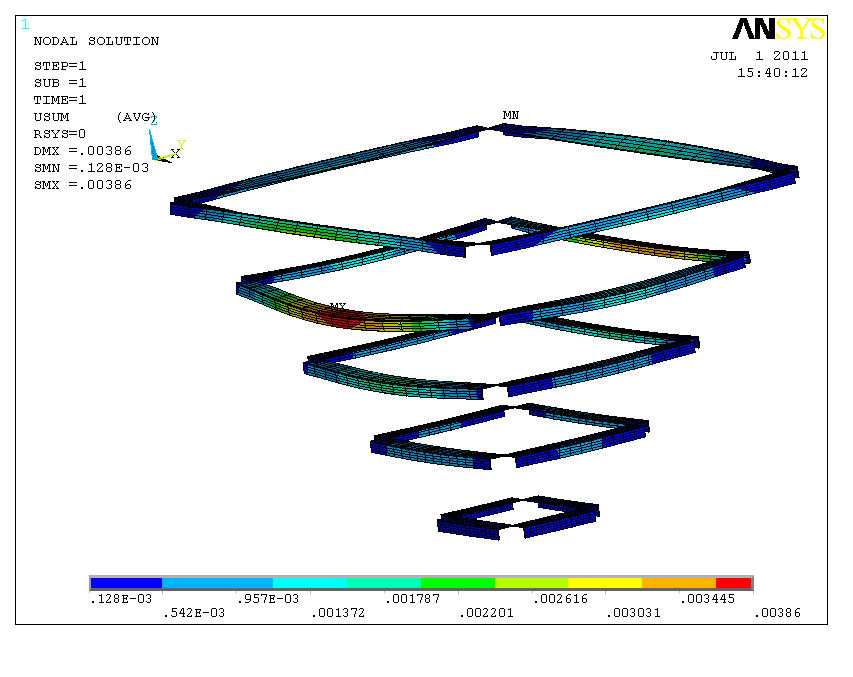
图0‑11 漏斗加劲肋的位移图

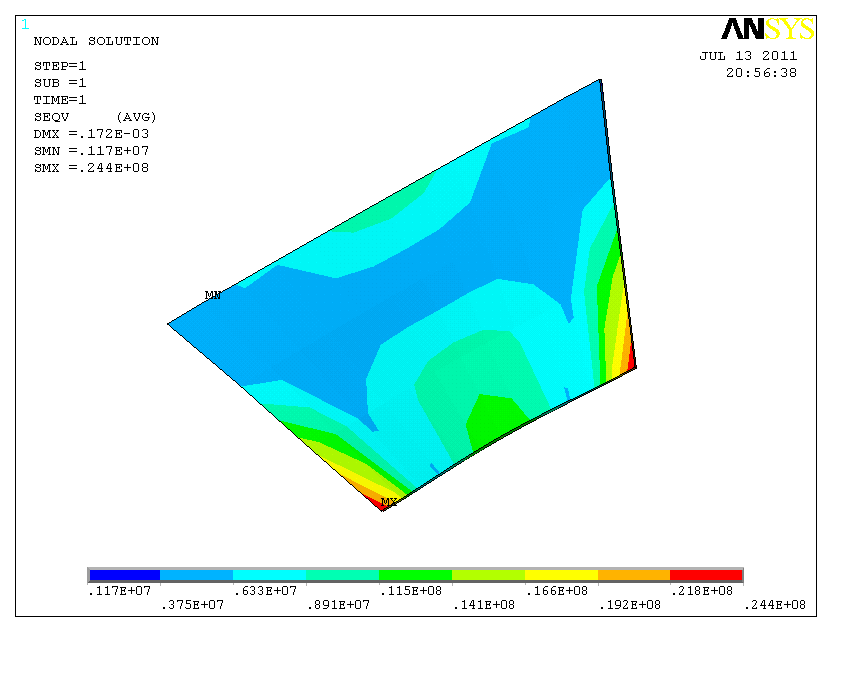
图0‑12 漏斗底部壁板的应力图

图0‑13 漏斗底部加劲肋的应力图

本章小结

本章首先介绍了有限元法的计算原理，然后应用ANSYS有限元软件对2个钢筒仓进行受力分析，得出以下结论：

1. 筒仓漏斗的壁板最大应力出现在壁板上部，且在跨中。

2. 筒仓漏斗的壁板最大变形出现在壁板上部，且在跨中。

3. 筒仓漏斗的加劲肋最大应力出现在顶部第二根，且在跨中。

4. 筒仓漏斗的加劲肋最大变形出现在顶部第二根，且在跨中。

规范计算结果与有限元计算结果的对比分析

结果对比

表3.1 规范方法与有限元方法计算结果对比表

结果分析

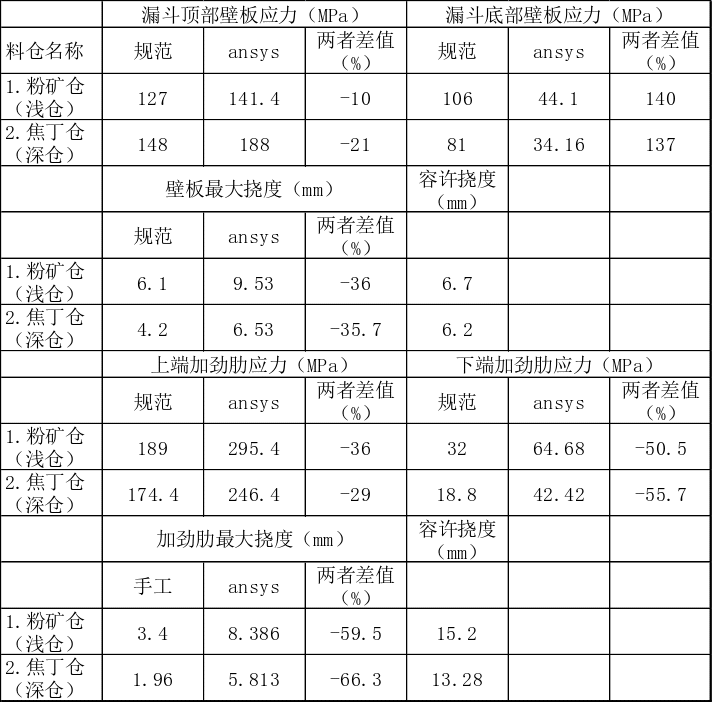
1. 壁板应力：壁板顶部应力计算值有限元法计算结果大于规范法，底部应力值有限元法计算结果小于规范法。原因如下：

1. 有限元应力计算根据变形协调条件，应力计算结果是多个方向空间应力的向量叠加，以其中一个方向为主应力，其余应力依次叠加。而规范计算方法只能算出平面内一个方向的应力，多方向的应力叠加结果大于一个方向的应力值。

2. 有限元方法的最大值往往出现在板块的边缘地带，因为有限元单元网格划分比较细致时，可以考虑应力集中。

3. 规范的计算原理将实际模型简化，假设壁板为四边固定的双向板或者是单向板，跨中弯矩的计算公式偏保守，同时忽略板面的轴向内力。

4. 有限元计算底部板块时，由于底部单元划分粗糙，造成节点之间的距离较大，导致单元应力信息捕捉的不完整性。同时由于荷载只作用在节点上，对于该板块而言部分应该作用在板面上的荷载转移到边缘，从而导致此块板面的计算结果偏小，因而计算值小于实际值。

解决方法：减小壁板应力有效的办法是减小水平加劲肋之间的距离和加大壁板的厚度；

2. 壁板挠度：两种方法的计算结果表明壁板挠度最大值均位于壁板上部，有限元计算结果数值大于规范法。原因如下：

1. 规范法计算壁板变形时是计算上下两排加劲肋间板块的变形，而有限元法的变形结果值是将壁板及加劲肋作为整体，最终结果为两者变形累加值。

2. 壁板的变形是在加劲肋变形的基础上进一步的变形累计值。

解决方法：在水平加劲肋间距不改变的条件下，减小钢板位移最有效的方法是在水平加劲肋中间设置竖向加劲。竖向加劲肋将壁板的区隔减小，壁板的计算跨度减小后，位移减小；需要说明的是增加竖向加劲肋不会对水平加劲肋的受力状况有任何改善。

3. 加劲肋应力：加劲肋应力计算结果有限元法大于规范法，有限元计算结果中应力最大的加劲肋为顶部第2排，规范方法的计算结果中应力最大的加劲肋位于顶部第1排。原因如下：

1. 有限元根据变形协调条件计算，壁板的最大位移出现在漏斗的中上部，加劲肋与壁板协同变形，所以此处加劲肋位移也较大，由应力计算公式 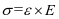得出，应变较大的部位，应力也相应增大，所以有限元计算结果，壁板及加劲肋的位移及应力最大值均出现在漏斗的中上部。

2. 规范计算加劲肋的位移公式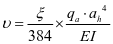 ，漏斗上部加劲肋跨度大于下部跨度，上部应力小于下部应力，由公式可知，位移与应力q为1次方增长关系，而位移与跨度为4次方增长，所以位移计算的最大值出现在上部第一根加劲肋，由于材料处于弹性阶段时，应力与应变成正比，所以加劲肋位移最大的部位，应力值也最大。

解决方法：减小加劲肋应力的有效方法是加大加劲肋水平向的宽度。采用角钢做加劲时，有角钢垂直于壁板和角钢水平摆放两种方式，就提高截面的抵抗矩而言，角钢垂直于壁板更好一些，但是角钢端部的刚性构造比较难以实现，因此在实际工程中更倾向于角钢水平放置。

4. 加劲肋挠度：加劲肋挠度计算值有限元法大于规范法。原因如下：

1. 有限元计算方法是将壁板和加劲肋作为一个整体，计算两者变形的累加值，规范法是把每一排加劲肋看成一个闭合框架，根据其承受的法向线荷载及跨度计算位移。

解决方法：减小加劲肋变形的有效方法是加大加劲肋的截面，增加加劲肋水平向的长度。

结论与展望

结论

本文采用ANSYS有限元分析软件对2种储料钢筒仓的受力性能进行了建模计算，并与我国规范简化方法的计算结果进行对比分析，得出以下结论：

1. 钢筒仓规范简化方法的计算结果表明，壁板最大应力及变形出现在漏斗顶部的跨中部位，加劲肋的最大应力和挠度出现在顶部第1根加劲处跨中部位。

2. 钢筒仓有限元软件的分析结果表明：壁板最大应力出现在漏斗顶部的跨中部位，壁板最大位移出现在漏斗中上部第2~3根加劲肋之间的跨中部位；加劲肋的最大应力和挠度出现在顶部第2根加劲的跨中部位。

3. 除壁板底部外，规范方法计算结果比有限元结果小30-60%。最大值出现的位置也有所不同，有限元方法的结果相比规范方法的结果下移大约1个加劲肋间距。由于有限元法的计算结果与ANSYS建模时对网格单元的尺寸划分，加载方式及荷载的种类等许多参数相关，所以建议设计人员在应用有限元软件计算钢筒仓时应采用不同的设计参数对同一模型多次计算，选用数据收敛的计算结果，然后将此结果与规范方法计算结果对比分析，综合两种方法的特点，得到最适合实际工程应用的结果。

展望

本文采用手工计算和有限元分析两种计算方法对矩形钢筒仓的结构行为进行了研究，得到了一些具有理论意义和对设计工作有所帮助的结论。不过钢筒仓结构的受力特性相当复杂，我国有关钢筒仓研究的规范手册也相对较少，要想完全清晰地分析计算其结构行为，还有许多进一步的工作要做。

1. 本文中的荷载仅局限于钢筒仓静载的分析，相关研究表明：物料偏心卸料、装料时在仓中的流动对仓体所造成的影响，往往是导致钢筒仓结构破坏的主要原因。所以对散粒体材料在筒仓中的运动形态及其他动力荷载的研究，则成为科研工作者一门重要的课题。

2. 流动的散粒体是筒仓结构中最常见的贮存物料，它既不同于连续固体，又不同于连续流体，在震动荷载作用下将呈现非常复杂的运动性态，并与筒仓结构的本体产生复杂的动力相互作用，给筒仓结构的动力特性带来很大的影响。动力作用的影响也是筒仓结构需要考虑的一个因素。

3. 风荷载对卸料结束后的筒仓影响很大，空仓时，风荷载应是作用在筒仓结构上影响最大的荷载。在装满物料时，由于筒仓的自重远大于风荷载，所以风载对结构的影响不大。

参考文献

1. 藤锦光, 赵阳. 钢筒仓转折环梁的稳定设计准则[J]. 空间结构, 2002, 6(4)

2. 中华人民共和国标准. GB50322—2001[S]粮食钢板筒仓设计规范. 北京: 中国计划出版社, 2001

3. 藤锦光, 赵阳. 大型钢筒仓的结构行为与设计[J]. 土木工程学报2001, 34(4)

4. 蒋莼秋. 世界筒仓设计规范动向和技术发展[J]. 特种结构, 1991, 4

5. 陈辉. 圆形水泥钢筒仓有限元分析及其在工程中的应用. 武汉: 武汉理工大学图书馆, 2006

6. 崔元瑞. 我国贮料构筑物建设的发展与回顾[J]. 特种结构, 2000, 17(1)

7. 贮仓结构设计手册编写组. 贮仓结构设计手册（第一版）. 北京: 中国建筑工业出版社, 1999

8. 中华人民共和国标准. GB50077-2003[S]钢筋混凝土筒仓设计规范（第一版）. 北京: 中国计划出版社, 2003

9. 归衡石, 丁官年. 钢结构钢筒仓-筒仓内各作用计算. 粮食流通技术, 2000, 4: 10-14

10. 归衡石. 钢筒仓倒塌事故和贮料流动影响. 冶金矿山设计与建设, 1999, 31(5): 50-63

11. 曾青, 王国鸿, 肖万松. 基于ANSYS的矩形钢筒仓有限元分析. 固体力学学报, 2008, 29(专辑): 60-63