日内时变性贝塔值估计研究

日内时变性贝塔值估计研究

廖俊煌

（肇庆学院 经济与管理学院 副教授 广东肇庆 526061）

摘 要：文章采用滚动式异质方差回归方法估计短期日内系统风险值，发现上证180高、低贝塔值指数和380高、低贝塔值指数的系统风险偏好呈现时变波动性；当贝塔值呈现不稳态，其回归均值是比较不可信赖的参考值，需及时更新。

关键词：时变性贝塔值；180指数；380指数

中图分类号：F830

一、引言

资本资产定价模型（Capital Asset Pricing Model；CAPM）为现代财务金融领域的主流理论之一，模型中的贝塔值被广泛使用来衡量系统风险偏好。贝塔值也可用来评估股票的合理价值、计算公司的财务资本成本，以及评估基金投资组合的绩效优劣。实务上应用股价报酬率来估计CAPM市场模型时，通常遇到股价报酬率呈现非正态分布问题，波动集聚造成异质方差的问题违背了回归假设条件，因此，采用异质方差回归模型来修正此问题实有必要。然而，金融市场时刻保持变动，贝塔值是常数的假设显然不符合现实，因此，采用时变性贝塔值来追踪更新系统风险值实有其必要，此为本文的研究重点。

有关时变性贝塔值的估计方法可参考Ciner（2015）^[1]的探讨比较，该研究明白指出贝塔值不是常数，而且随着时间推移表现出显著变化。承续学者的看法，本研究重点着眼于股价指数报酬率的时变性贝塔值估计，属于微观经济领域，宏观经济因素并不在本文的研究范围内。本文假设市场信息已经反应在股价及指数报酬率上，股票市场至少符合半强势效率市场的特征。用当前实时的股价及指数报酬率估计贝塔值，可及时正确反应当下投资人的市场风险偏好。

研究对象为代表大型股的上证180高贝塔值指数（代码000135）、180低贝塔值指数（代码000136），和代表中小型股的380高贝塔值指数（代码000137）、380低贝塔值指数（代码000138）等四种指数。各指数的编制分别以其各自母指数为样本空间，根据各股票在过去一年期间表现计算出来的贝塔值进行排序后，取排名靠前180、380，与靠后180、380的股票分别作为样本股计算指数。高、低贝塔指数系列的股票表征其与全市场不同的价格属性变化，定期提供给投资人比较基准和投资标的参考。唯一要注意的是该贝塔值是以过去一年为计算期间得到的一个平均值，而本文估计的是短期日内时变性贝塔值。

二、研究模型与假设

研究设计采用滚动式异质方差市场模型(Rolling Garch Market Model，RGMM)。首先，依据CAPM理论建立GARCH（1,1）市场模型如下：

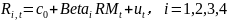（1）

（2）

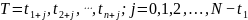(3)

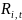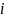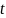其中，自变数 分别是第 种指数的对数报酬率， 是上证指数对数报酬率,符号 表示时间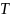， 为估计期间， 为观察值总个数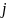， 为滚动估计次数。式（1）为均数方程，式（2）校正方差群聚效应，并考虑前一期t-1的记忆方差 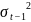，是为条件方差方程。每次估计需检验 值是否显著异于0；滚动式估计之下， 值将依序生成时间序列，借由观察序列值变化可得短期趋势。

三、实证结果

实证数据采用60分钟K线股价指数报酬率为研究标的，每次估计期间用营业日20天的60分钟收盘对数报酬率值共80个观察值。数据取自同花顺看盘软件，期间跨度自2020年9月11日至2021年6月30日期间共768笔，各序列均滚动估计689次，实证软件为Eviews 9；各收益率序列通过单位根检验均显示稳态，为节省篇幅，结果省略但可提供。

经过配适全部期间768笔观察值的Garch（1，1）阶模型，假设检验显示 显著异于0，回归残差LM检验显示不再有ARCH效应， 检验显示残差已无自我相关现象，整体模式显著，表示采用Garch（1，1）阶模型是合宜。接续改变并使用滚动式估计，可生成时变性 时间序列,如图1表示。实证各 序列得知：5%显著水平下，Jarque-Bera检验呈现非正态分布；Ljung-Box Q统计检验均呈现自我相关现象；Kernel密度分布发现呈现不同的峰值；ADF检验得知只有380低贝塔值序列呈现稳态。结果发现：日内系统风险值不是稳定的值，呈现时变性。以180高贝塔值序列为例，统计689个滚动 估计值，均值为1.3493，标准差为0.2079，极大值为1.8037，极小值为0.8926，明显呈现上下波动；另3个贝塔值序列均有类似的特性。综合以上得知系统风险值短期具有不稳定的特性。

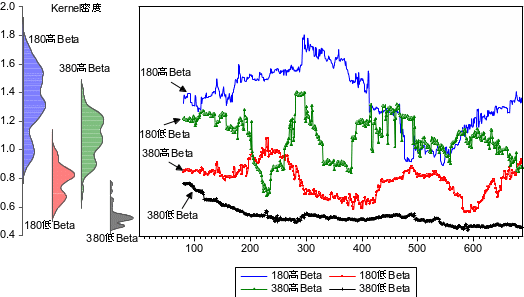
图1：时变性系统风险值

四、结论

一年期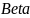 值是过去一年期间表现出来的一个均值，通过估计其短期值得知

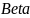值具有时变波动的特性。既然会波动，借由正负偏离均值来适度调整投资组合实有其必要。

参考文献

[1] Cetin Ciner. Time variation in systematic risk, returns and trading volume: Evidence from precious metals mining stocks [J]. International Review of Financial Analysis，2015, 41：277-283.

Study on time-varying beta estimation of stock price return

Abstract: This paper uses the rolling conditional heterogeneous regression method to estimate the short-term systematic risk. It is found that the risk preference of market investors for the Shanghai Stock Exchange 180 high and low beta indices and 380 high and low beta indices is time-varying. When the time-varying beta is unstable, the regression mean is an unreliable reference value.

Key words: Time-varying Beta; 180 index; 380 index

1