讷河市第一中学 161300
摘要:同余是高中数学竞赛中的基础知识,同余概念是初等数论的重要组成部分,竞赛中的很多题都要用到同余理论,怎样能更好的理解同余概念、掌握同余计算对竞赛备考生有很大帮助。本文从生活实例出发,讲述同余概念及其运算。
关键词:同余 同余运算 同余化简
在以12为周期的时钟上,只有12个数。11点再两个小时后,指向1点。超过12点要减去12的倍数。记为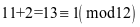 该运算有加法运算,且满足加法交换律、结合律。还可以有乘法运算,乘完的结果超出12,减去12的倍数后数仍然在1到12之间,如
该运算有加法运算,且满足加法交换律、结合律。还可以有乘法运算,乘完的结果超出12,减去12的倍数后数仍然在1到12之间,如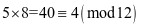 ,
,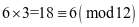 ,
,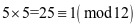 。
。
一、同余的概念

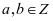 ,
,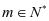 ,
,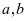 除以
除以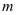 若余数相同,则称
若余数相同,则称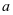 与
与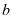 关于模
关于模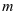 同余,记作
同余,记作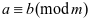 。否则,就说
。否则,就说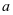 与
与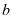 关于模
关于模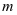 不同余,记作
不同余,记作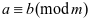 。
。
显然,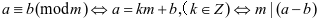
同余的性质:同余具有自反性、对称性、传递性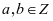 ,
,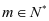
①自反性: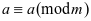
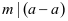
②对称性: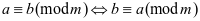
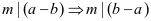
③传递性:若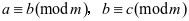 ,则
,则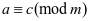
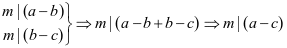
二、同余运算
1、加、减、乘、乘方运算
⑴若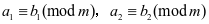 ,则
,则
①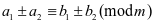
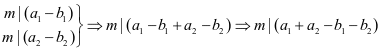
特别地: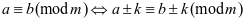 ,
,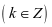
②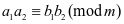
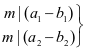
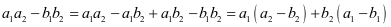
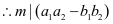
特别地: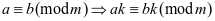 ,
,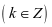
③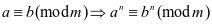 ,
,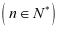
⑵设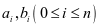 ,
,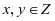 ,
,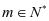 ,
,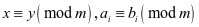 ,则
,则
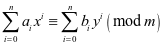
推论:设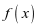 是一个整系数非零多项式,
是一个整系数非零多项式,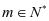 ,
,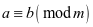 ,则
,则
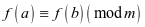
⑶若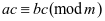 ,则
,则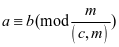
特别地: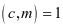 时,
时,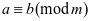 (可除性)
(可除性)
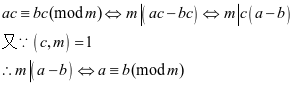
特别地: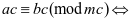
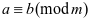
⑷若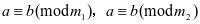 ,且
,且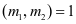 ,则
,则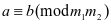
若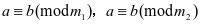 ,且
,且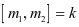 ,则
,则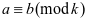
2、化简技巧
⑴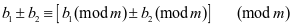
⑵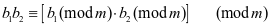
⑶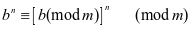
⑷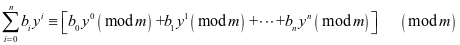
⑸计算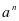 :
:
方法一:求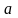 的多少次幂关于模同余于
的多少次幂关于模同余于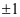
若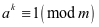 ,带余除法得
,带余除法得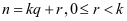
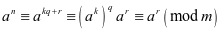
方法二:任何正整数乘方得个位数重复出现的周期为4,即
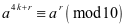 ,其中
,其中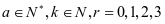
方法三:欧拉定理
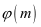 表示不大于
表示不大于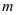 且与
且与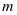 互素的数的个数
互素的数的个数
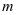 的标准分解式
的标准分解式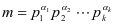
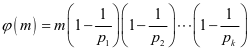
若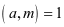 ,
,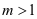 ,则
,则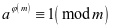
方法四:费马小定理
设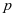 是素数,
是素数,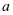 是正整数,则
是正整数,则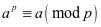
设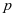 是素数,
是素数,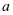 是正整数,且
是正整数,且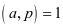 ,则
,则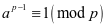
例1. 求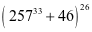 被50除的余数
被50除的余数
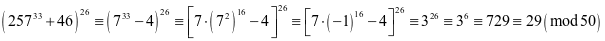 所以余数为29
所以余数为29
例2.求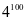 被19除的余数
被19除的余数
由费马小定理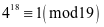
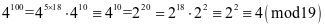 所以余数是4
所以余数是4
例3.求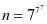 的个位数
的个位数
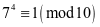
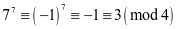
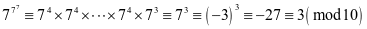
例4.试证明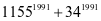 不是平方数.
不是平方数.
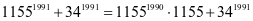
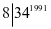 ,
,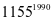 为平方数,奇数的平方是8n+1型,
为平方数,奇数的平方是8n+1型,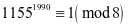
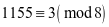
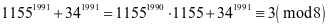 ,所以不是平方数
,所以不是平方数
三、生活中的应用
1、同余解释天干地支纪年
天干:甲、乙、丙、丁、午、己、庚、辛、壬、癸,分别记为1,2,3,...,10。
地支:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥,分别记为1,2,3,...,12。
已知公历年份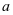 ,求对应干支。
,求对应干支。
设天干为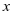 ,地支为
,地支为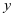 ,则
,则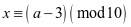 ,
,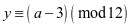
如公元184年黄巾起义,计算其干支。
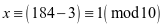 ,故天干为甲
,故天干为甲
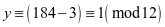 ,故地支为子
,故地支为子
因此公元184年为甲子年,所以黄巾起义时在官府门前都贴有“甲子”字条,口号为“岁在甲子,天下大吉”。
又如今年2020年,求对应干支。
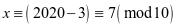 ,故天干为庚
,故天干为庚
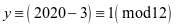 ,故地支为子
,故地支为子
故今年为庚子年。
2、同余解决星期问题
在公务员、事业单位、银行等考试中,有一种很常见的题型,它出现频率高,那就是星期问题。尽管这一类问题相对比较容易,但很多学员却认为它很麻烦,很绕,常常将其放弃,其实这类问题用同余知识能够快速清晰的求得答案。
如:1986年(2月9日)是星期日,请问再过1988天是星期几?再过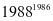 天是星期几?
天是星期几?
问题分析:我们知道,日期问题本质上是一个循环问题,循环周期是7,过了多少天是星期几,其实就是转化为过得天数除以7,看所得的余数是多少,然后从原星期的基础上向后或者向前推余数天,就是问题的答案。
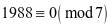 ,可知再过1988天仍然是星期日
,可知再过1988天仍然是星期日
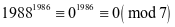 ,可知再过
,可知再过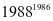 天仍然是星期日
天仍然是星期日
四、结束语
本文主要从探讨同余定义、性质、相关定理及其应用入手,突出同余理论在初等数论中的地位,同时用实例表明同余理论在解决看似复杂的问题上是有明显的优势和便利性的。同时我们也要将理论知识应用于日常生活,从而真正意义上的理解运用同余的性质,真正体会到同余的魅力。