基于几何模型的反射面优化研究Research on reflector optimization based on geometric model

基于几何模型的反射面优化研究 Research on reflector optimization based on geometric model

高泰恒 李萌奇 李贺 刘焱

山东协和学院，山东省济南市 250109

摘要：射电望远镜是通过接受外太空光线得到天体信息的一种科学设备^[1]。我国的FAST天眼是世界最好的射电望远镜。对于FAST天眼，我们将探讨以下问题：在前先研究方向的基础上，通过计算调节后的馈源舱的接收比来与基准反射球面的接收比相比较，可以先计算调节后馈源舱的接收比，再算出基准反射球面的接收比。通过这两个接收比的比较来回馈不同的参数和方法，确定怎样调整能够成为最优解，使结果达到最优。

关键词：几何模型 旋转抛物面 Python 整网控制

1.研究背景

射电望远镜的工作原理是通过主动反射面的调节将接收到的无线电波反射在位于反射面焦点的馈源舱上，馈源舱采集反馈信息，用作研究。而反射面的调节工作直接决定了工作抛物面是否接近理想抛物面，同时也决定了所接收到的无线电信号和天体的射电波是否处于最佳效果，所以主动反射面的形状最佳调节问题至关重要。

2.理想抛物线的确定

由于被观测体距离地球极为遥远，发出的光线可以视为平行光，因FAST是由多个小块组成，所以反射面剖面可以近似看作抛物线，要使平行光尽可能汇聚于馈源舱，以基准球面的球心为原点，经过基准球心且切于球面的射线作为x轴，SC 轴作z轴，建立平面直角坐标系，最终建立如图1的几何模型。

近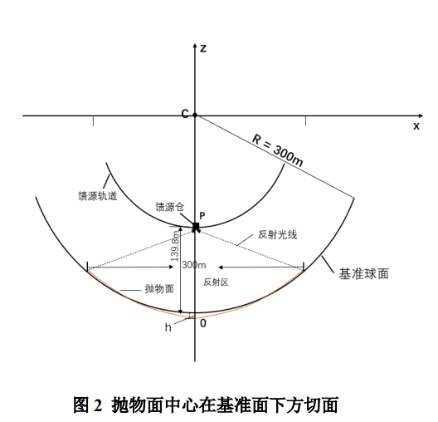

似旋转抛物面的焦点已给出，因促动器径向伸缩范围为±0.6米，所以相对于基准面最低点，抛物面顶点变动范围为±0.6米，本文将对抛物线顶点相对于基准面位置进行两种讨论。

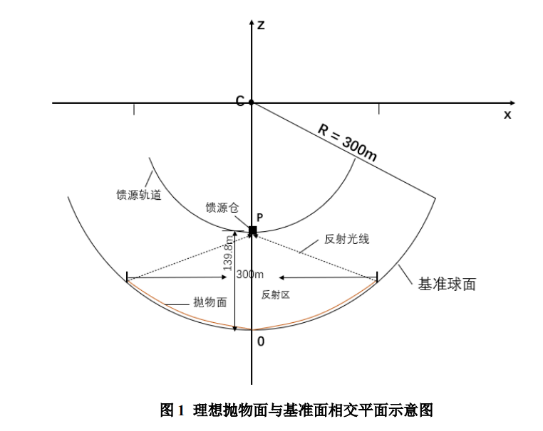
图1 理想抛物面与基准面相交示意图 图2抛物面中心在基准面下方切面

3.抛物线顶点不在基准面的几何情况分析

如果抛物面顶点在中心 O 下方，具体如图2所示：

本文以球心C为坐标原点，CP延长线为z轴，建立空间直角坐标系，因为P为焦点，且焦距已确定。由几何模型计算，以z轴为旋转轴，经过计算可得理想抛物面方程为：

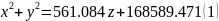
3.1抛物线顶点与中心重合情况

如果抛物面顶点与中心O重合的情况下，只需求得焦距，再根据焦距即可求得该平面抛物线方程，以Z轴为旋转轴即可求得理想抛物面的方程。

当坐标原点在球面最低的中心位置时，F=0.466R，则焦距OP=139.8m。

即可求得平面抛物线的方程，则：

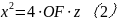
以z轴为旋转轴通过计算得理想抛物面方程为：

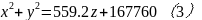
综上所述，根据抛物面顶点位置的不同可以得出以上两种几何模型，具体为公式（1）和公式（3）。

3.2模型检验-抛物面与基准面的高度差值

因为基准面为球面，其截面方程为：

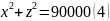
由于实际操作对促动器高度有要求，故应对抛物线形变进行检验，因为抛物面和基准面都是在相同高度时对称的，所以对沿y轴方向上的截面进行高度差求解，设高度差为h，当抛物线顶点在基准面上时，通过沿x-o-z面截取抛物面和基准球面，得

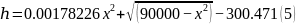
通过Python对公式(5）进行最大值、最小值、图像模拟。因其图像在基准面之上，只拟合其大于0的情况。得之在x=106时两方程差为0.653m，满足题意。在此情况下促动器变化大，考虑到反射面是由一个个小平面组成，所以此模型连续性较差。

在抛物线顶点在中心下时，沿x-o-z面截取抛物面和基准球面，得

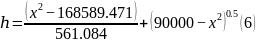
利用Python对公式(6）进行最大值、最小值、图像模拟，得出在x = 115时两方差最大为0.21，最大伸缩量为0.53，满足题意。因在这种情况下促动器变化最小，所以抛物线顶点在中心之下几何模型最优。综上所述，两种理想模型都符合题意。

4.对于一般情况下的FAST几何状态分析：

假定待观测天体𝑆位于𝛼 = 36.795°, 𝛽 = 78.169°时，对其状态进行求解。

4.1利用基准面确定理想抛物线

由于天体不再位于基准球面正上方，因此理想抛物面也要随之改变。因为天体角度已给出，所以只需求出的理想旋转抛物面的旋转角度，将图一中的椭圆旋转。利用抛物面中心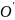 为原点。将原点平移到C点即可求出基于C点的抛物面方程。

焦点C不随着理想抛面的改变而改变，因此在抛面移动的过程中，C点始终固定^[2]。可根据C点的位置确定抛面移动后的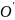中心 ，由中心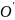 的位置即可确定抛物面的方程。

4.2 利用方位角研究理想抛物面距圆心的位置

由于使用笛卡尔坐标系对旋转抛物线难以表示，故决定采用极坐标系来表示抛物线方程。以基准面圆心C为坐标极点，以天体与基准面球心连线为极径，以此推出一焦距为141.3米的抛物线^[3]。由几何计算得：

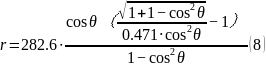
r为圆心距抛物线距离，θ为相对于极径的角度。

5.总结与展望

本文对射电望远镜索网反射面的几何形态做了相对完整的分析，对反射面的形状调节这一问题根据相关因素建立模型，对调节的规划和对最优方案的达成有着较为新颖的见解。

参考文献：

[1]胡金文,朱丽春.FAST反射面测量样机中反射镜对摄影测量算法的影响分析[J].科学技术与工程,2014,14(16):190-194.

[2] 王志远. 基于迭代学习理论的FAST整网控制策略的研究[D].东北大学,2015.