山东协和学院 山东济南 250107
摘要;内容摘要:乙醇可以被催化剂催化生成C4烯烃。本文针对催化剂组合与反应温度影响生成C4烯烃的问题,基于多元线性回归分析建立线性回归模型,分析催化剂、温度与C4烯烃之间的关系,利用三者的关系预判消耗量与生成量,调整化学反应策略,最后给出反应方案。
关键词: C4烯烃 回归模型 多元线性回归分析
催化剂会诱导化学反应发生改变,而使化学反应变快或者在较低的温度环境下进行化学反应,因此催化剂在现代化学工业中占有及其重要的地位。C4烯烃在化工产品及医药生产中使用范围广泛,选择乙醇作为原料生产制备C4烯烃,在制备过程中,将Co负载量、Co/SiO2和HAP装料比、乙醇浓度组合在一起称为催化剂组合,催化剂组合与反应温度会对C4烯烃的选择性和C4烯烃收率产生影响,因此通过对催化剂组合的不断设计,探索乙醇催化偶合制备C4烯烃的工艺条件具有非常重要的意义和价值。本文通过建立数学模型,拟通过对乙醇催化生成C4烯烃的反应进行判断,得到判断化学反应的线性回归模型。
一.分析研究:乙醇转化率、C4烯烃的选择性与温度的关系
首先,选取性能数据表作为数据来源,以温度为自变量,乙醇的转化率和C4烯烃的选择性为因变量,借助MATLAB对数据进行可视化处理。然后,通过分析图像,确定线性关系,建立一元回归模型[1]
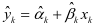 ,
,
用最小二乘法对模型进行求解。对回归模型进行显著性检验,确定模型的正确性。最后,对350度时给定的催化剂组合的测试数据表中的数据进行分析,得到反应物的转化率与各生成物的选择性与时间变化的关系。
数据可视化
为了更好的研究乙醇的转化率、C4烯烃的选择性与温度的关系,将性能数据表中的催化剂组合编号、温度、乙醇的转化率、C4烯烃的选择性四项数据提取出来,借助MATLAB软件做出相关的数据散点图,选取其中4种催化剂组合A1,A2,做出如图1—图2乙醇与C4烯烃含量变化图:
| |
图1 A1组乙醇与C4烯烃含量随温度变化图 | 图2 A2组乙醇与C4烯烃含量随温度变化图 |
以上两张图像以温度为自变量,以乙醇的转化率与C4烯烃的选择性为因变量,总体呈现为线性回归的趋势,分析该图像可以得知随着温度的增高,乙醇的转化率也会随之增高,C4烯烃的选择性也会随之增高,符合线性回归模型要求。
计算相关系数
借助MATLAB软件,结合乙醇转化率与C4烯烃选择性变化图中的数据,求得乙醇转化率和C4烯烃的选择性与温度变化的相关系数r。表1为乙醇转化率和C4烯烃的选择性与温度关系的部分r值表:
表1 乙醇转化率和C4烯烃的选择性与温度关系r值表
催化剂组合 | A1 | A2 | B1 | B2 |
相关系数r (乙醇) | 0.9321 | 0.99 | 0.9254 | 0.8633 |
相关系数r (C4烯烃) | 0.7869 | 0.7869 | 0.9718 | 0.9698 |
由表中数据可以得知,所有相关系数均大于0.5,在中度相关以上,而且大部分r的值大于0.8,为高度相关,也就是说相关系数r的存在是合理的,即该图像变化趋势符合线性变化趋势,确定乙醇转化率、C4 烯烃的选择性与温度的关系是线性关系。
模型的建立
因为乙醇转化率与C4烯烃的选择性变化基本相同,不失一般性,这里以乙醇转化率为研究对象,建立一元回归模型:
| (1) |
其中yk表示第k组的乙醇转化率,αk,βk表示回归系数,xk表示第k组的温度,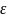 k表示随机误差,且
k表示随机误差,且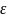 ~N(0,β2)。
~N(0,β2)。
根据公式(1),建立yk关于xk的线性回归方程:
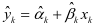 ,
,
其中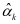 ,
,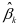 分别表示αk,βk的估计值。
分别表示αk,βk的估计值。
模型的求解
我们用最小二乘法[2]来估计αk,βk的值,使得残差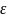 k的平方和最小,而残差的平方和为
k的平方和最小,而残差的平方和为
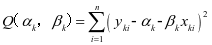 ,
,
此时:
| (2) |
根据公式(2)可以得知, 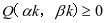 且可导,得出:
且可导,得出:
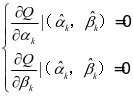 ,
,
求解上式可得:
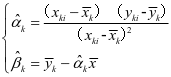 。
。
其中,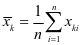 ,
,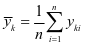 。
。
利用MATLAB进行求解得到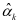 ,
,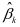 ,如下为关于乙醇转化率关于温度的回归方程:
,如下为关于乙醇转化率关于温度的回归方程:
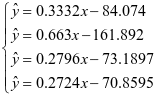 ,
,
同理可得关于C4烯烃的选择性的回归模型,下式为关于C4烯烃的选择性的回归方程
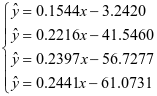 ,
,
得出结论:乙醇转化率、C4细听选择性都与温度成正相关的线性关系,即在大多数情况下,它们会随着温度的升高而升高。
二.分别研究:催化剂组合及温度对乙醇转化率以及C4烯烃选择性影响
分析性能数据表,将与其他催化剂组合不同的石英砂的催化剂组合设置为对照组。研究变量间的关系,建立多元线性回归模型[3]。
分析建立模型需要得知的数据,设出模型的初始形态,再对模型进行化简,利用向量法与最小二乘法求得各回归系数与最小误差的值,即得到模型最终解。基于多元线性回归模型的基础上,借助MATLAB求得乙醇转化率的复相关系数与C4烯烃的选择性的复相关系数,由此检验该模型的合理性。基于该模型求出乙醇转化率与C4烯烃的选择性大小的变化。
数据分析
分析性能数据表,了解各种催化剂的组合以及各种催化剂组合对应的温度变化情况,其中存在着一组具有石英砂的催化剂组合,即A11组,通过查阅资料可以得知,该组中1wt%Co/SiO2主要含SiO2,且石英砂主要是由SiO2组成,而且该组合中不存在HAP,于是将该催化剂组合当作没有HAP的对照组。
分析该数据表中的其他催化剂组合,可以得知不同的催化剂组合其中的Co 负载量、Co/SiO2 含量 、HAP 含量、乙醇浓度有不相同的,因此可以将这四种因素看作是变量的存在形式,考虑温度变化对其产生的影响,温度也看作是一种变量,因为这五个变量的关系是多元的、对乙醇转化率与C4烯烃选择性是成线性相关的,以此为基础建立多元线性回归模型。
模型的建立
在五个自变量已知的基础上建立多元线性回归模型:
| (3) |
因为C4烯烃选择性的估计值计算方式与乙醇转化率相似,于是这里以乙醇转化率为对象,建立关于乙醇转化率变化的模型。
其中:xi1为第i次Co的负载量,xi2为第i次实验Co/SiO2的重量,xi3为第i次实验HAP的重量,xi4为第i次实验乙醇浓度,xi5为第i次实验温度高低,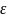 为随机变量对yi造成的影响,
为随机变量对yi造成的影响,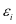 符合模型假定,借助向量法对该模型进行求解,求解式列如下所示:
符合模型假定,借助向量法对该模型进行求解,求解式列如下所示:
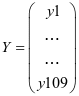 =
=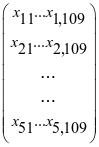
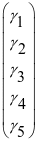 +
+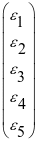 ,
,
分析上面公式可以得到回归模型,模型可以表示为:
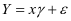
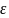 (0,
(0,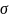 2E),
2E),
化为正规方程组为(在x可逆的情况下):
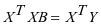 。
。
模型的求解
根据最小二乘法估计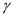 值记作
值记作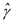 使
使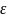 的平方和最小,即:
的平方和最小,即:
| (4) |
解公式(3)可得:
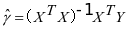 ,
,
由此解得关于乙醇转化率的线性回归[4]模型:
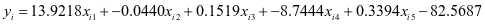 。
。
因为C4 烯烃选择性的估计值计算方式与乙醇转化率相似,所以,同理可得关于C4 烯烃选择性的线性回归模型:
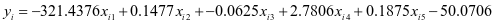 。
。
由它们各自的回归系数的估计值确定,Co负载量的升高会使乙醇转化率增大,C4烯烃选择性减小,CO/SiO2含量的升高会使乙醇的转化率减小,C4烯烃选择性选择性增大,HAP的含量升高会使乙醇的转化率增大,C4烯烃选择性减小,乙醇浓度的升高会使乙醇转化率减小,C4烯烃选择性增大,温度的升高会使乙醇转化率与C4烯烃选择性都增大。
模型的检验
根据定义有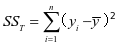 ,
,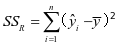 ,
,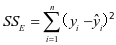 此时,它们的自由度
此时,它们的自由度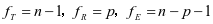 ,且
,且
R2= 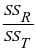 。
。
利用MATLAB进行求解得,乙醇转化率的复相关系数为0.7962,同理得出,C4烯烃选择性与自变量之间的复相关系数为0.7331,这说明回归变量与响应模型的关系密切,即模型合理。
[参考文献]
司守奎,孙玺菁.数学建模算法与应用(第三版)[M].北京:国防工业出版社,2021.109-120.
刘宝东,宿洁,陈建良.数学建模基础教程[M].北京:高等教育出版社,2015.201-220.
吕绍沛.乙醇偶合制备丁醇及C_4烯烃[D].大连:大连理工大学,2018.
韩中庚.数学建模算法及其应用(第三版)[M]北京:高等教育出社,2017.120-140.