重庆市璧山中学校
问题1:函数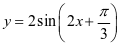 是三角函数吗?
是三角函数吗?
学生独立思考,抽取一位学生回答,并要求其说出理由.
(预设答案1)生:不是.
师:请说出为什么.
生:我们将正弦、余弦、正切函数称为三角函数,这个函数不是正弦函数,更不是余弦、正切函数.
(预设答案2)生:是.
师:理由是它带了三角符号 么?请同学们翻开教材178页认真阅读,再请同学起来回答.
么?请同学们翻开教材178页认真阅读,再请同学起来回答.
【设计意图】三角型函数与三角函数有区别,三角型函数是三角函数通过复合而来,本质为复合函数,学生对此易混淆.其次强调阅读教材的重要性,并指出阅读理解能力也是高考考查的关键能力.
问题2:按照函数的研究方法,我们应该怎样来研究这个新函数来把握它的本质.
师:请同学们回忆研究指数、对数、三角函数的图象与性质的思路是怎样的?
生:根据函数定义研究函数图象,再结合图象获得性质,从而把握这个函数的本质,再将此函数应用到实际生活中模型的建立.
【设计意图】明确研究函数的一般思路(从定义出发作函数图象,再借助图象研究函数性质),为后续函数的学习提供方式方法.
问题3:如何研究一个函数的图象?请同学们结合三角函数思考.
生:首先是作出函数图象,进一步观察图象特征,从图象中获得函数性质.
师:总结起来就是作图——识图——用图的这样一个过程.
师:请同学们结合教材及新课的学习,回顾正弦函数图象的作图过程,思考:正弦函数相比于之前学的函数在作图中遇到了哪些困难,是如何解决的?
教师播放展示正弦函数的作图过程.
生:第一个,定义域 上的图象范围太大,利用了周期性将其缩减为
上的图象范围太大,利用了周期性将其缩减为 作图;第二个就是怎么描点的问题,由以前经验计算描点已不再适用,因而借助了单位圆中正弦的定义描点作图.
作图;第二个就是怎么描点的问题,由以前经验计算描点已不再适用,因而借助了单位圆中正弦的定义描点作图.
师:余弦函数图象呢,怎样得到的?
生:利用诱导公式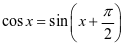 将正弦函数图象向左平移
将正弦函数图象向左平移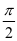 个单位.
个单位.
师:也就是说通过图象变换得到的.
(师)总结:正弦函数借助定义,利用性质描点作图;
余弦函数通过变换作图(平移);
师:图作出来,如何观察函数图象特征呢.按照以往经验来说,从宏观到微观,从整体到局部.
师:从整体来看,函数具有周期性、对称性,从左往右看,函数具有“上下起伏”刻画的单调性,从上往下看,函数有最值,从关键部位看,函数有零点.
学生完成知识框架并展示.
师:以上性质的获得是通过观察图象而来,其实也可以利用单位圆性质来发现,在教材探究部分有给大家展示.除了直接观察、几何直观的角度,还能通过其它方式获得吗?
生:还可通过代数运算得到,周期性、奇偶性利用诱导公式可证.
师:很好,其实单调性、最值仍可通过导数运算,在后续会有学习,通过代数运算还可得到正弦恒等变换,这样的式子: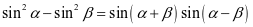 ,抽象为
,抽象为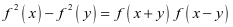 ,有兴趣的同学可下去研究一下.
,有兴趣的同学可下去研究一下.
【设计意图】明确研究图象的路径:作图——识图——用图,为函数图象的研究提供一般方法.作图过程回顾正弦函数图象的获得,引导学生回想作图遇到的困难是通过何方法解决的,也是正弦函数与之前学习函数的区别所在,总结三个函数图象的获得是有区别的,学生明白图像的获得可有多种方式的同时,也为下节课做好铺垫.识图过程教会学生观察图象(如何观察,观察什么),进而获得函数性质.
问题4:如何快速作出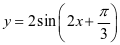 的图象,获得性质.
的图象,获得性质.
师:此处我们能否像正弦函数一样描点作图呢,描哪些点呢?
生:五点法.
师:为何可用“五点作图法”呢?
生:能通过代数运算将其化为正弦函数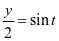 即
即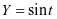 与一次函数
与一次函数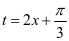 .
.
师:哪五个点呢?请同学们在导学案上利用五点法完成图象的绘制.并按刚才观察图象特征的方式写出该函数性质.
学生完成并展示.(教师强调函数定义域为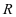 ,图象需要左右延展.)
,图象需要左右延展.)
师:这个图象还有其他方式可得到吗?
生:变换作图.
师:很好,但是具体怎么变换呢,欲知后事如何,请听下回分解.在5.6节呢会给大家详细介绍.
师(总结):此处我们通过研究函数图象获得了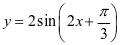 的性质,也就完成了研究一个新函数的基本流程.
的性质,也就完成了研究一个新函数的基本流程.
【设计意图】让学生明白“五点作图法”是在实际解决具体问题中借助图象分析思路的有效方法,可快速地帮我们作图、识图;并让学生明白形如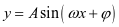 的函数可用五点作图法的本质是可通过代数运算转化为正弦函数.
的函数可用五点作图法的本质是可通过代数运算转化为正弦函数.
问题5:在不作图的情况下,如何求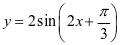 的周期、对称性、单调性、最值及
的周期、对称性、单调性、最值及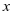 的值.
的值.
学生在导学案上完成并展示.
师(总结):此处将变量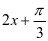 整体代换为
整体代换为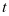 ,利用正弦函数
,利用正弦函数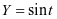 的图象解决,即通过变量代换实现化归的思想方法.
的图象解决,即通过变量代换实现化归的思想方法.
【设计意图】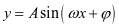 正弦型函数的基本思路是把
正弦型函数的基本思路是把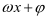 看作一个整体,通过变量代换的方式转化为正弦函数解决,在此过程中帮助我们掌握化归与转化、数形结合的思想方法,切实操作提高分析问题,解决问题的能力.
看作一个整体,通过变量代换的方式转化为正弦函数解决,在此过程中帮助我们掌握化归与转化、数形结合的思想方法,切实操作提高分析问题,解决问题的能力.
问题6:是不是仅有三角函数才有周期性呢?
生:不是.
师(追问):你能举出其它周期函数吗?
生: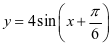 .
.
师:除了这种类型的函数呢?
生:教材214页18题的函数.
师(追问):很好,那这个题解析式就交给大家下来求吧.那你能再举出无最小正周期的函数吗?
生: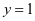 .
.
师(追问):三角函数是作为描述周期现象的重要数学模型,周期性具有十分重要的地位和作用,那么请同学们思考,周期性对研究函数有什么用呢?
生:周期可缩短函数研究范围,将定义域上的图象缩减为一个周期来研究.
师:回答得很棒,同学们都很优秀.老师也希望同学们能将今天所学应用于今后的数学学习中,其实呢,数学是位迷雾中带着面纱的仙女,拨开那层迷雾,其实你会发现它很美.
数学是爱大家的,希望大家爱上数学!
【设计意图】单独提出周期性,不仅在于周期性为新学性质,更在于让学生明白三角函数作为描述周期现象的重要函数模型,其周期性具有十分重要的地位和作用,它能在研究函数图象、性质时缩减到一个周期来研究,同时指出生活中还有许多其他的周期函数.
师:请同学们跟着老师的节奏回顾本堂课所学.
总结:
(1)我们是如何把握一个新函数的本质(研究函数的一般思路)?
(2)周期性是三角函数最重要的性质,有什么作用?如何去用?
(3)函数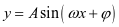 的图象怎么画?性质如何得到?
的图象怎么画?性质如何得到?
提升练习
请同学们结合三角函数图象及性质,完成如下问题:
1.函数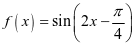 在区间
在区间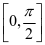 上的最小值为( )
上的最小值为( )
A.-1 B.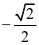 C.
C.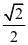 D.0
D.0
(多选)2.已知函数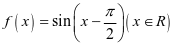 ,下列结论正确的是( )
,下列结论正确的是( )
A.函数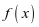 的最小正周期为
的最小正周期为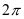
B.函数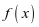 在区间
在区间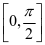 上是增函数
上是增函数
C.函数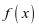 的图象关于直线
的图象关于直线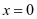 对称
对称
D.函数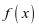 是奇函数
是奇函数
3.求函数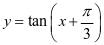 的定义域
的定义域
4.已知函数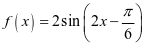 .
.
(1)求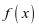 的最小正周期;
的最小正周期;
(2)求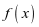 的最值及对应
的最值及对应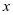 的值;
的值;
(3)判断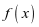 在
在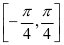 的单调性;
的单调性;
(4)求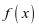 的对称中心坐标、对称轴方程.
的对称中心坐标、对称轴方程.
作业布置:教材214页13,14,15,16,18题