拥堵热点区域交通信号配时优化

白函鹰

中国 伦敦大学学院

摘要：在有限的城市路网供给条件下，精细化的交通管控是解决供需失衡所致拥堵问题的有效技术手段之一。数据驱动式的交通信号配时优化，对于提高交通管控的质量水平、缓解交通拥堵和提升交通运行效率有重要意义。断面检测作为传统信号配时优化数据来源，存在空间覆盖率低、建设和维护成本高等局限性，移动检测技术的蓬勃发展为交通信号配时优化提供了新的数据支持。在此背景下，综合利用海量多源的检测数据实现交通信号配时的智能优化成为交通管控领域的前沿课题。

关键词：交通控制；信号配时优化；排队长度

1排队长度预估方法

1.1基于车辆轨迹数据的排队长度估计方法

排队长度均指最大排队长度，是指从进口道停车线开始向上游最后一辆排队车辆启动离开排队的位置之间的距离，以长度为单位进行量化。在高渗透率环境下，大量车辆轨迹数据得以实时获取，时段内各周期均可观测到停车和非停车两类车辆轨迹，因此可以直接利用轨迹数据提供的信息，结合交通流运行特性进行动态排队估计。模型是基于以下的假设条件建立的：

（1）对交通运行状况的假设，本文提及的交通拥堵表现为周期有剩余排队，不包含路段溢流这种极端过饱和情况；

（2）不考虑路段上不同车道排队的相互阻挡和干扰；

（3）认为同向多车道的排队长度不存在较大差别，如存在较大差别以同向车道的最大排队长度为主；

1.2基于车辆轨迹数据和车牌识别数据的排队长度估计方法

在渗透率较低或路网可获取轨迹的车辆分布不均匀时，某些路段在部分周期无法采集到车辆轨迹样本，在这种缺少样本的情况下，单纯依靠车辆轨迹数据估计得到的排队长度信息无法满足工程精度要求，因此需要引入其他数据进行辅助。由于交通管理的需要，交叉口号牌识别检测器在我国大部分城市的覆盖率都较大且数据较为容易获取，是对车辆轨迹数据的有益补充。构建综合利用号牌识别数据和车辆轨迹数据的排队长度估计模型

（1）分别利用历史累计的号牌数据和轨迹数据提取排队相关特征和排队位置信息，建立双层随机森林模型，对新输入的车辆号牌特征，进行车辆停车和非停车状态划分，并对排队停车的车辆进行停车位置估计；

（2）利用估计得到的车辆停车和非停车状态信息，基于LWR模型中的几何关系进行消散波特征点重构和排队上下极限值提取。

2 数据特征分析与预处理

2.1 车辆时位跟踪轨迹数据特征分析

基于车载GPS设备的车辆位置跟踪轨迹数据，是利用安装在车身的移动检测器，实时精确地提供车辆高分辨率位置信息的数据，这些数据不受地理位置的限制，为交通运行状态估计提供了强有力的数据支持。对于本文的排队长度估计而言，可以获取车辆与路段下游停车线的距离。时间戳提供车辆在当前位置的时刻，体现了轨迹在时间上的连续性，可以用一一对应的时间和位置信息在二维的时距图上描绘出车辆的行驶轨迹。瞬时速度直接反映了车辆的运行状态，可以通过历史数据统计得到的阈值划分车辆运行状态，即停车、低速行驶和自由流行驶。瞬时速度方向主要用于判断车辆在路段的走向，由于地图匹配存在误差，速度方向可以作为判断轨迹点处于路段正向或反向的重要特征。

2.2 交叉口车牌号识别数据特征分析

车辆号牌是车辆的唯一身份证明，通过号牌可以追溯到车辆的归属地和车辆主人的登记信息，对城市路网中的车辆进行号牌识别，是交通执法部门监督维护城市交通秩序的必要手段。号牌识别检测器一般布设在交叉口的进口道停车线附近，可以通过视频抓拍所有通过停车线的车辆，并利用图像识别技术获取车辆的牌照信息得到的数据称为车辆号牌识别数据，作为定点检测器获取的数据，受限于检测器布设范围和布设密度的影响，LPR数据并不能获取单个车辆在路网中完整的行驶轨迹，而只能获取车辆在一段时间内依次通过若干个交叉口的粗精度轨迹信息。

3 基于拥堵热点区域交通信号配时优化方法

3.1 路网交通控制问题描述

城市交通网络是由路段和交叉口两个元素组成拓扑结构，因此可以将其简化定义为由路段和节点组成的有向图。

设计一个控制器𝐶𝑖来决定在每一个时段𝑡内交叉口各𝑝𝑖∈𝒫𝑖对应的相位持续时间𝐺𝑝，该持续时间需要满足交叉口信号配时中对应流向最小绿灯时长的约束，和总的周期时长约束。优化的目标对于集中式控制和分布式控制策略是不同的，集中式控制策略的优化目标为路网各交叉口的集计指标，如路网各交叉口的总输出量最大，车辆总延误最小，车辆总的行程时间最小等；而对于本文提出的分布式策略而言，优化的目标是局部交叉口的交通运行状态，如交叉口的总流出量最大，交叉口总延误最小和总排队长度最小等。

交通控制方法是按固定时段为最小步长进行优化的，并且假设时段内的交通状况基本保持稳定（允许小幅波动）且时段内各信号控制交叉口的配时均为静态方案，因而估计得到的排队长度信息代表了一定时段内的车道的排队分布的统计值。对于更加精细化的管控而言，可以利用各周期的排队长度作为输入，动态地优化每个周期的控制参数，在这种应用情境下本文提出的控制策略也具有一定的可行性。

3.2 基于背压控制的交通控制方法

由于BP控制策略是一种分布式的控制方法，在实施上只需要考虑交叉口的单点优化，但是压力权重的引入也考虑到了优化交叉口与下游交叉口的关联性。对于关键交叉口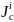 ，现状t时段各相位的有效绿时可以表示为𝑔𝑝(𝑡),𝑝∈𝑃𝑖，各相位的有效绿灯时间之和，加上总的绿灯损失时间为周期长度，针对时段t的优化决策参数为各相位的绿灯时间调整量，记作∆𝑝(𝑡),𝑝∈𝑃𝑖。假设关键交叉口 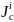共有N个流向，每个流向记作𝑀𝑗,𝑗=1,…,𝑁；每个流向的对应的流入路段和流出路段分别记为 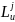和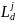 ，即车流从路段 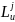流入交叉口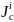 ，从路段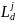 流出交叉口，对应绿灯调整后的流出量可以表示为：

𝜉𝑖(Δ𝑝, 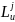, , 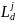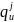)=min( 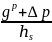, 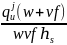) （3.1）

其中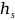 为车道饱和车头时距；𝑤为消散波波速；𝑣𝑓为自由流速度。根据交叉口进口车道排队估计值和排队容量上限，计算对应的排队压力值；将交叉口进出口路段的排队压力差值作为对应流向的排队压力释放权重，构建最大化关键交叉口流出量的规划模型，对关键交叉口的相位绿灯时间进行优化。

4 结语

本文以城市道路网络系统为研究对象，以车辆位置跟踪轨迹、交叉口车辆号牌识别、路网静态几何信息与多时段交通信号配时数据为基础，提出不同数据环境下的城市道路交叉口进口道车道（组）排队长度估计方法，以表征城市道路交通运行状态，并将其作为交通信号配时优化的状态输入参数。对车辆位置跟踪轨迹数据和交叉口号牌识别数据进行了特征分析，并提出了相应的数据预处理方法，为交通运行状态估计和交通信号配时优化算法提供了必要的数据支撑。在拥堵热点区域配时优化算法方面，针对路网拥堵热点区域的关键交叉口进行相位绿灯时间的优化。

参考文献

[1] 李攀. 基于动态数据的城市道路交叉口交通需求估计研究[D]. 南京: 东南大学, 2016.[2] 张彤. 拥堵状态下路段交通需求估计方法研究[D]. 济南: 山东大学, 2018.

[3] 袁长亮. 城市路网过饱和交通信号控制策略硏究[D]. 上海: 同济大学, 交通运输工程学院, 2007.

[4] 李铁舜, 徐建闽, 壬琳虹. 过饱和交通网络的多层边界控制方法[J]. 华南理学学报（自然科学版）, 2012, 40(7): 27-32.