基于FEKO软件实现目标动态RCS仿真

基于 FEKO软件实现目标动态 RCS仿真

王伟，徐康，王欢庆

中国人民解放军 94005部队，甘肃省酒泉市 735000

摘要：雷达目标检测、目标跟踪、目标识别、威胁评估、雷达的最大作用距离估计等方面，RCS都是极其重要的基本参数，本文以某飞机模型为研究对象，通过计算和分析构建了该目标的静态RCS数据库，在此基础上，通过动目标姿态轨迹数据生成或飞行实测数据、推导了雷达站心坐标系与目标坐标系之间的转换关系，得到了目标动态RCS仿真数据。该方法对雷达目标动态特性的仿真研究具有重要的参考价值。

关键词：静态RCS数据库 动态RCS数据库 坐标系转换

一、雷达散射截面积定义及影响因素

雷达散射截面积（Radar Cross Section,RCS）是表征雷达目标对于雷达入射波散射能力的物理量。雷达散射截面积的定义为单位立体角内目标朝接收方向散射的功率与从给定方向入射于该目标的平面波功率密度之比的4π倍，该定义假设目标在平面波照射下各向同性散射。

对于给定的平面入射波，其能量密度为

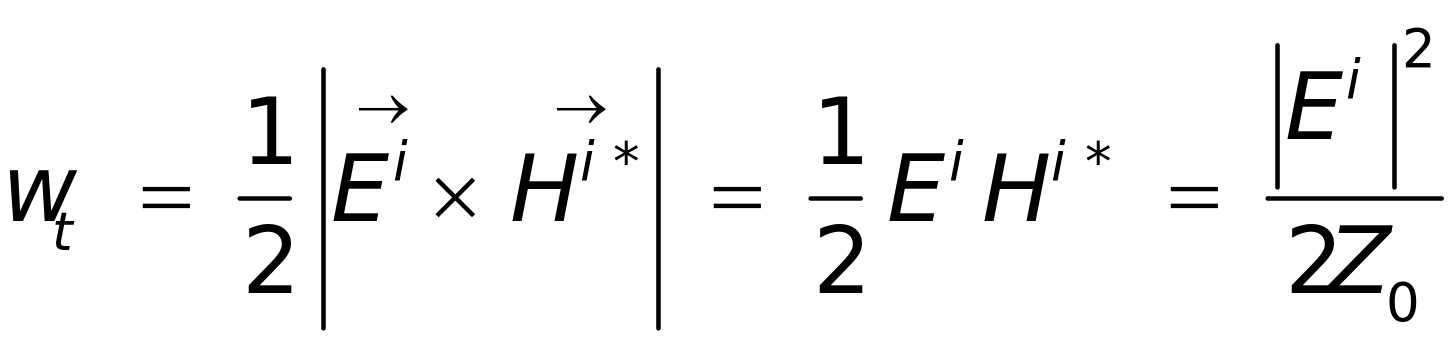（1-1）

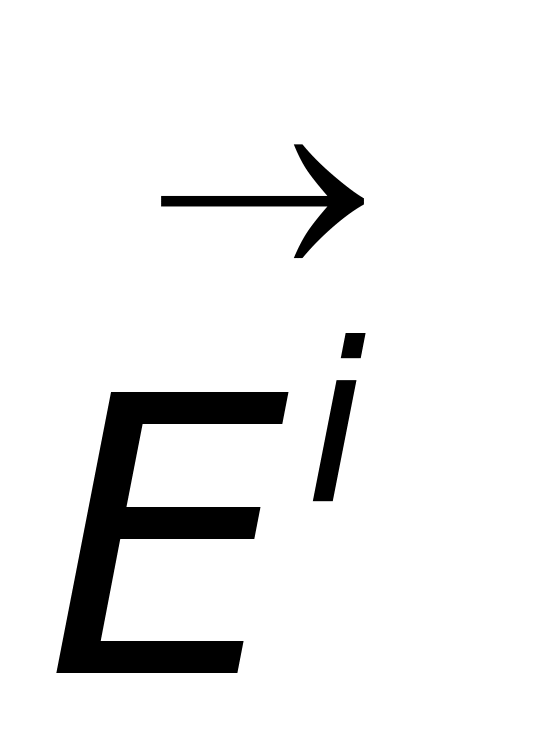式（1-1）中， 和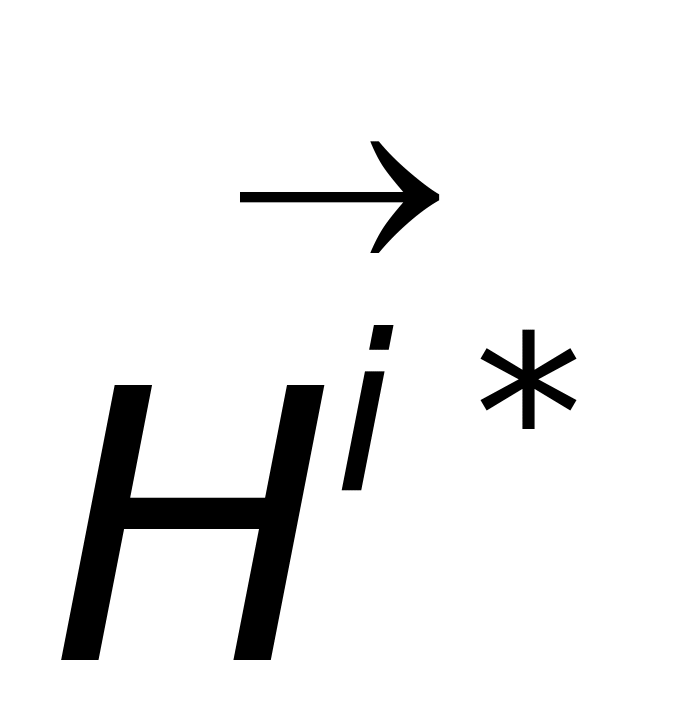 分别为入射波的电场强度和磁场强度，“*”号表示复共轭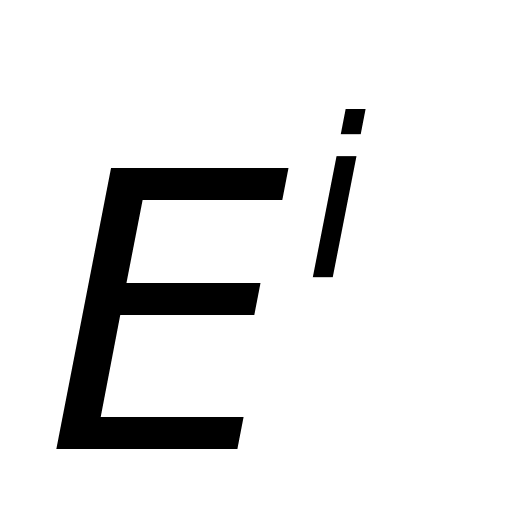， 和 为相应的复振幅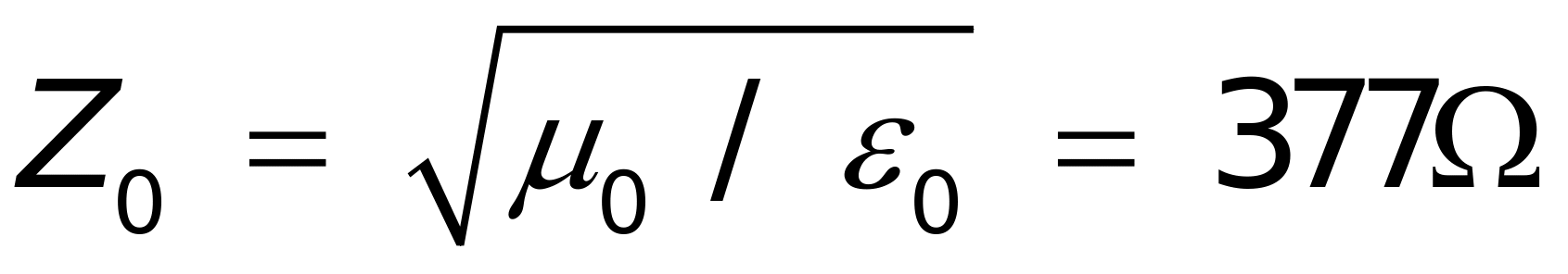， 为自由空间的波阻抗。

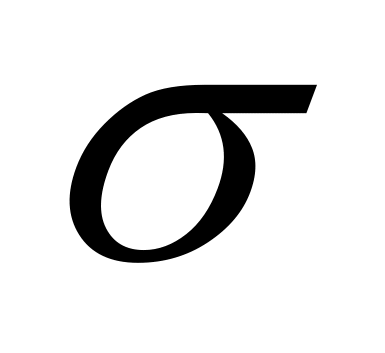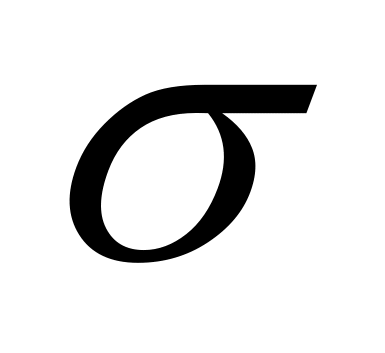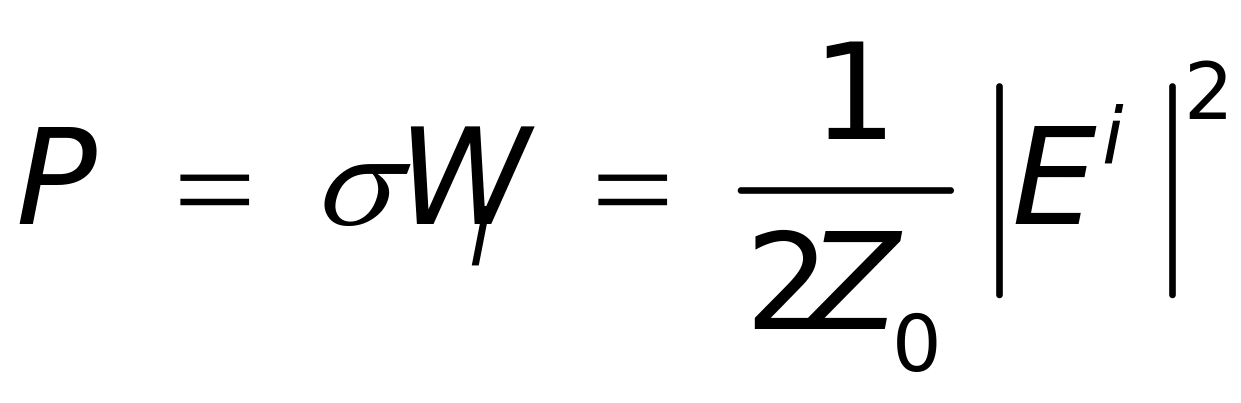对于RCS大小为 的目标，其所截获的总功率为入射功率密度与 的乘积： （1-2）

如果目标将该功率在空间中各向同性的散射出去，则距离目标R的位置对应的散射波功率密度为

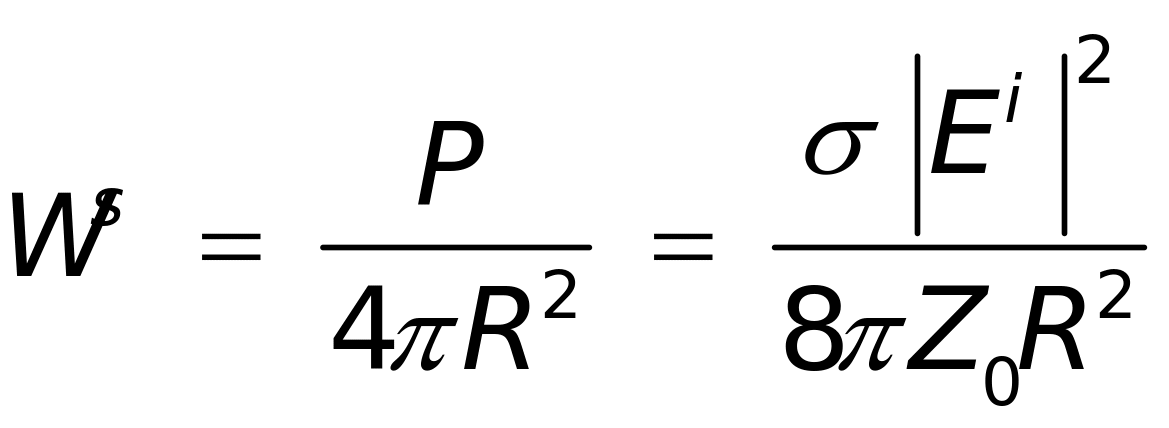（1-3）

若用散射电场强度表示散射波功率密度，则为

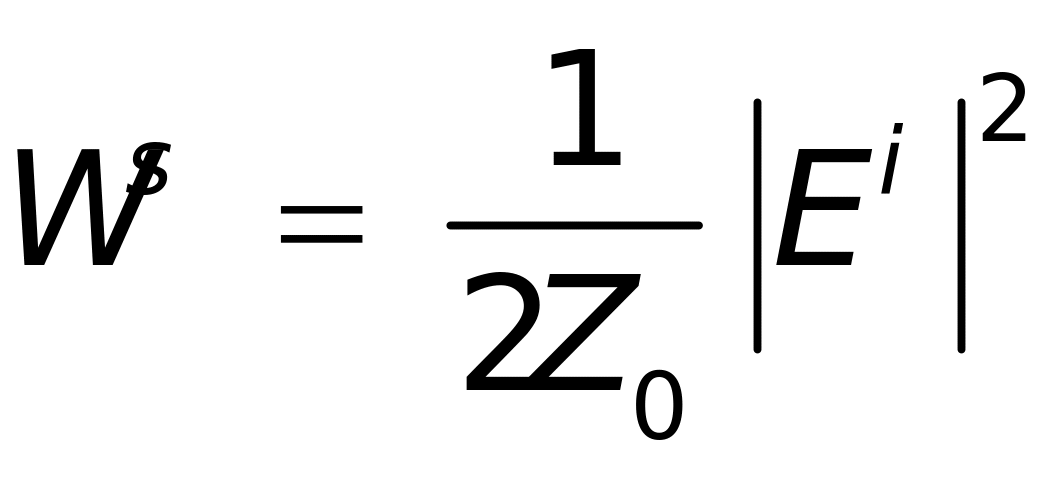（1-4）

则由式（1-3）和（1-4）相等，可以推出

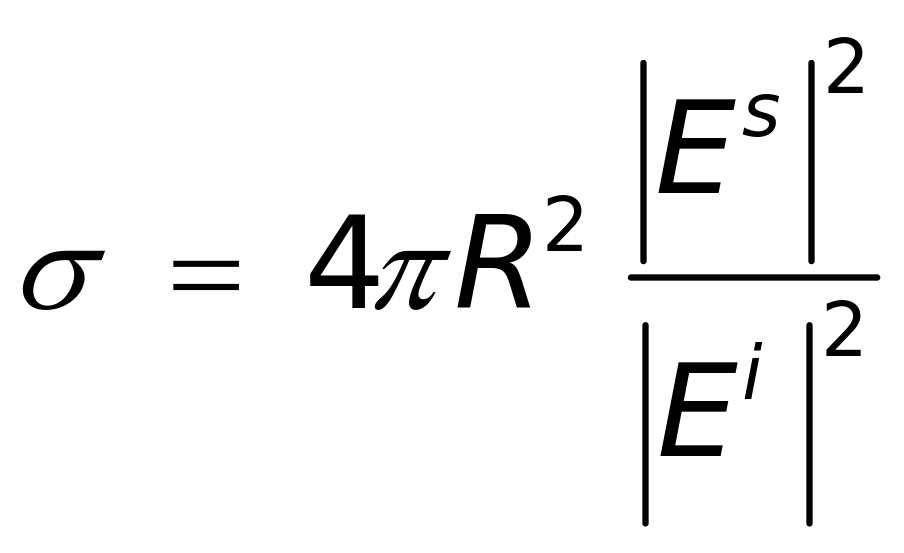（1-5）

因为入射波为平面波，当R趋于无穷远时，散射电场强度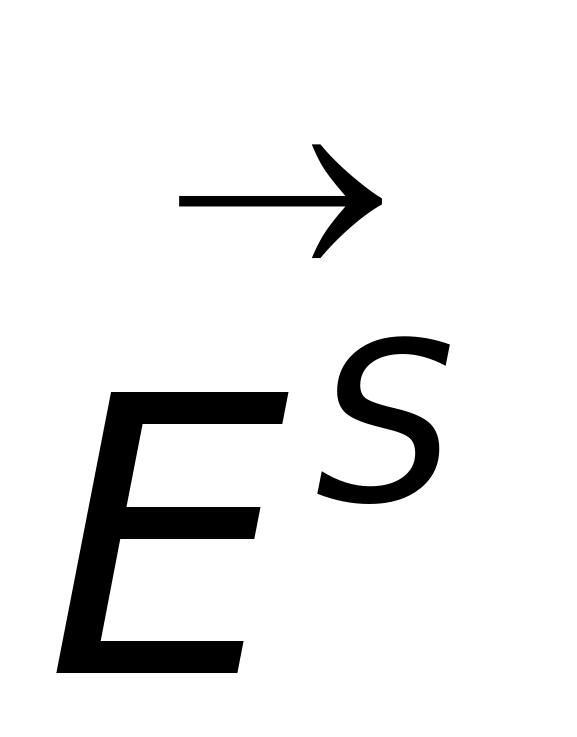 与R成反比，入射电场强度 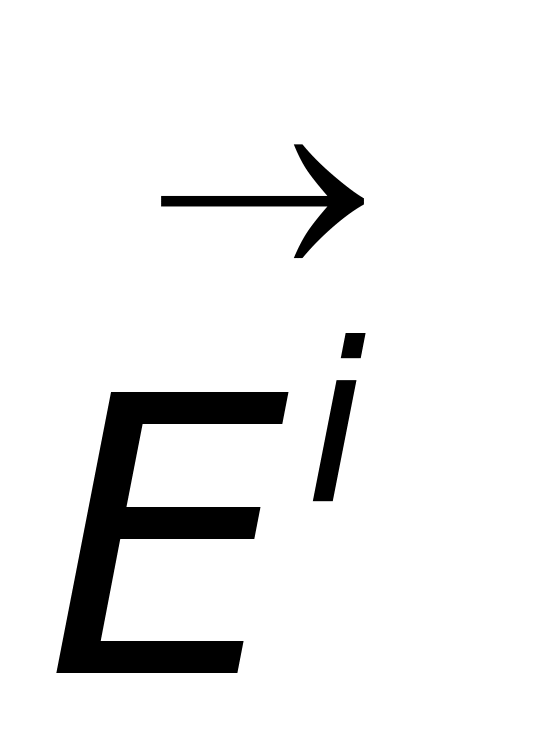与R成正比，这样 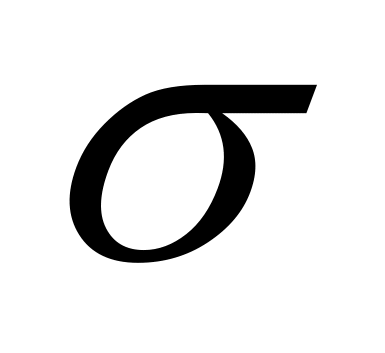与R无关。对于原厂RCS而言，式（1-5）应更严格的写为：

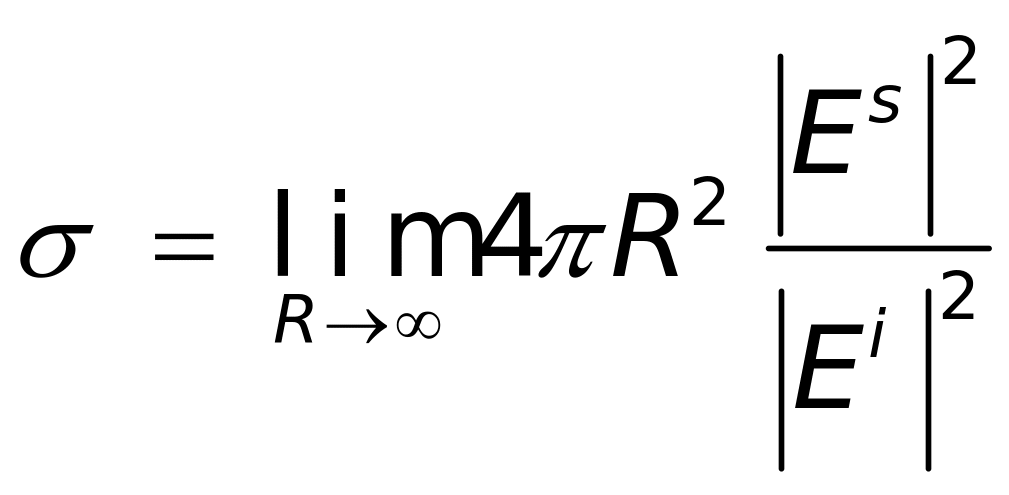（1-6）

由式（1-6）可知RCS为标量，常用的量纲为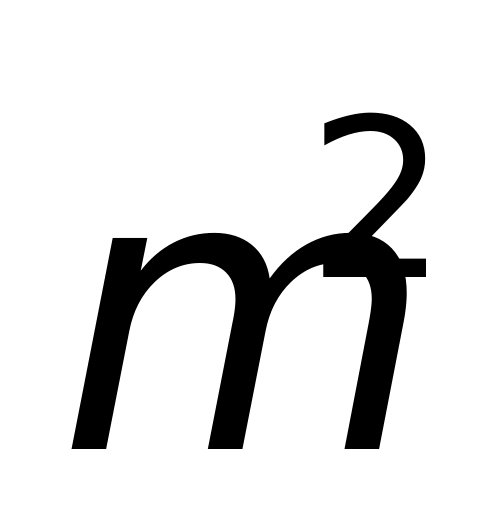 。在实际工程中常用其相对于1 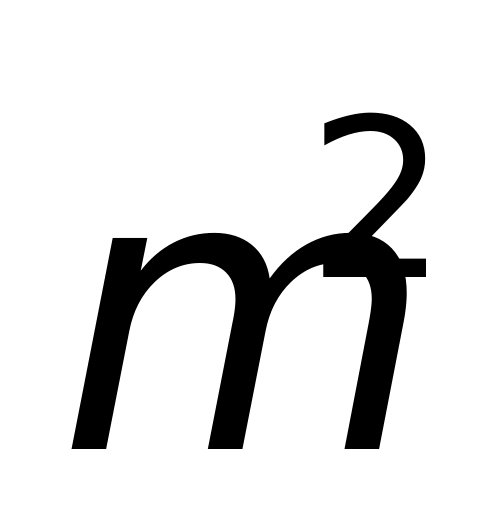的分贝数表示，即分贝平方米，记为dBsm，用来表示目标反射强度。

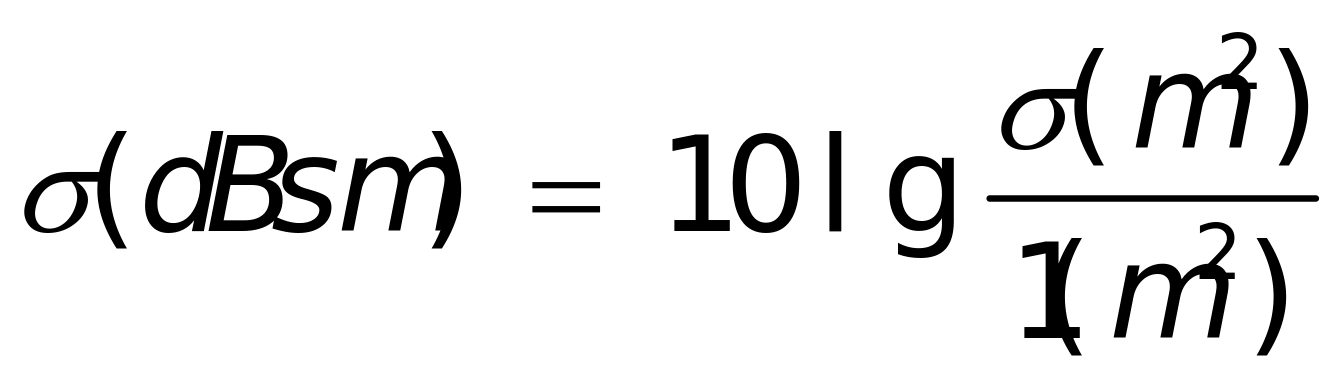（1-7）

二、RCS计算方法

散射场的计算方法大致可以分为三种：

第一种方法是电磁散射场的严格解，它作为经典的边值问题，根据Maxwell方程和边界条件在直角左边坐标、柱坐标、球坐标和其他正交坐标系中通过分离变量法求解。

第二种是散射场的近似解。由于能够得到严格解的形状实在是非常有限，人们不得不发展散射场的各种近似算法来解决更多的散射场的计算问题，例如，几何光学（GO）法、物理光学（PO）法、几何饶射理论（GTD）等。

第三种方法是数值解法。现代计算电磁学中的数值方法是随着计算机技术的进步而发展起来的一种计算方法，相比于早期的解析方法和近似算法，它具有不受物体形状限制，精度高，能适合各种实际工程的特点。数值方法按方程类可分为两类：一类基于偏微分方程，如时域有限差分法（FDTD）和有限元法(FEM)；另一类基于积分方程，如矩量法（MOM）等。该类方法以等效电流为未知元，只需在物体内部或表面划分网格，未知数目较少，且不受数值色散影响。

FEKO软件内置了多种电磁散射计算方法，主要有矩量法（MOM）、物理光学法（PO）、一致性几何饶射理论（UTD）、快速多极子求解方法（MLFMM）等。对于分析复杂结构的电磁问题，一般选用MOM法或MOM/MLFMM混合算法。本文中选用的是MOM/MLFMM混合算法求解飞机模型的RCS。

三、基于FEKO软件目标静态RCS建模与仿真

在计算复杂目标的雷达截面积（RCS）时，一个关键问题就是对研究的目标进行建模。发展到现在，复杂目标RCS计算的建模方法大致经历了以下三个阶段：

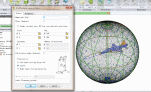
（一）简单几何体组合模型法；（二）平面三角面元模型法；（三）参数表面模型法。FEKO还可以通过与多个专业三维设计软件（如CAD、ANSYS等）接口，导入它们建立的三维模型，也可直接导入划分好网格的文件。本文通过将已有的三维飞机模型导入FEKO软件中进行RCS计算。在FEKO中采用MOM/MLFMM混合算法,雷达方位角变化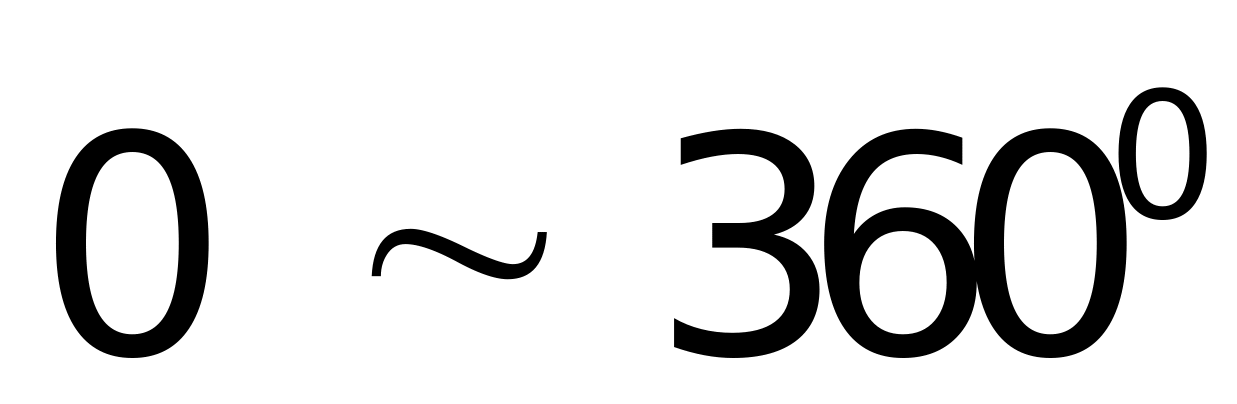 ,俯仰角变化 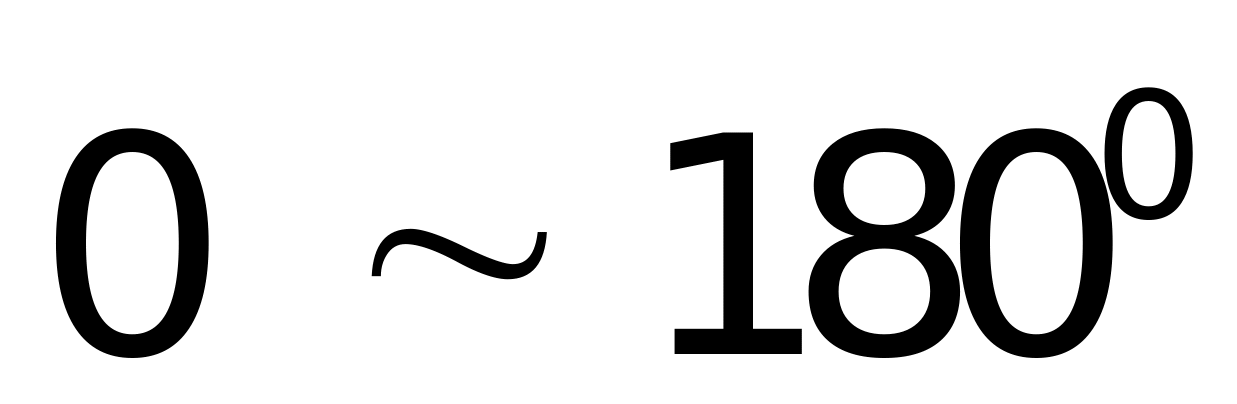。雷达频率50MHZ，采用平面入射波。

、

图1 FEKO中雷达视线角的设置

图（2）、图（3）分别给出了雷达分别在水平极化（HH）、垂直极（VV），方位角变化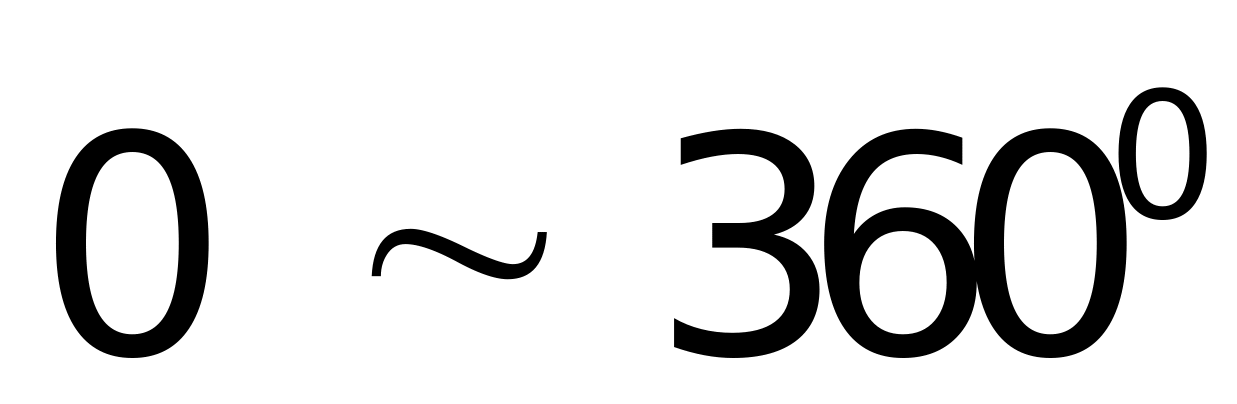 ，俯仰角为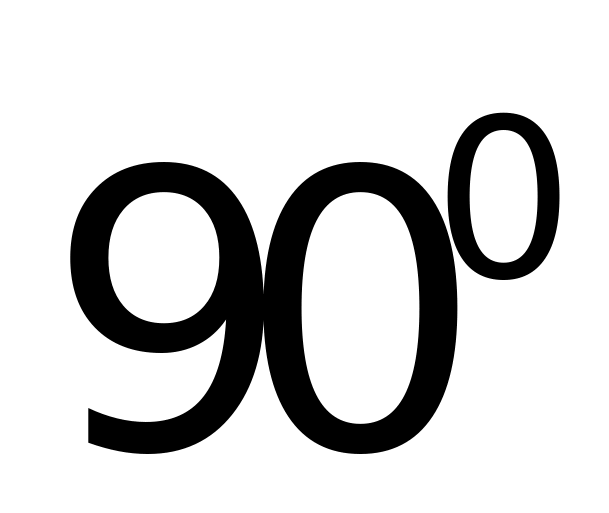 照射飞机模型的RCS强度曲线。

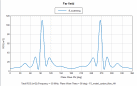
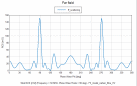
图2 飞机模型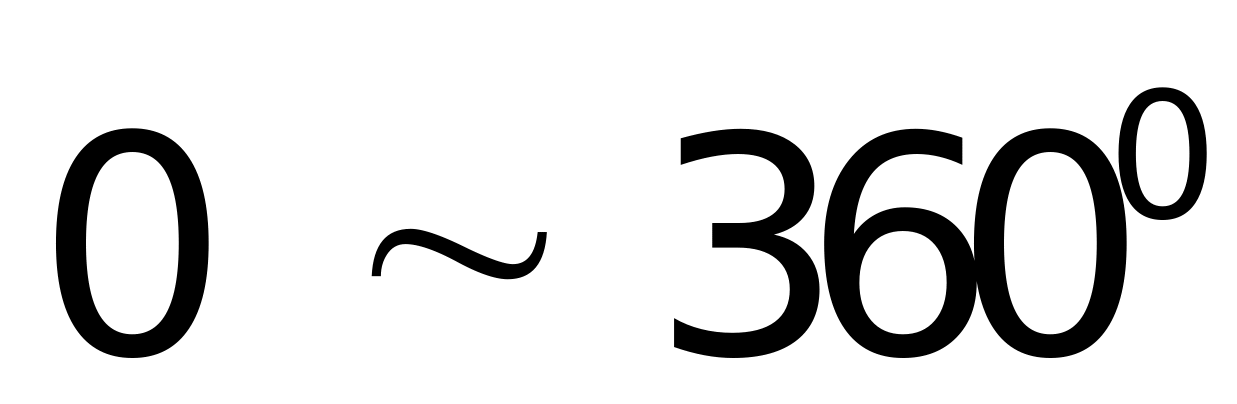 RCS强度曲线（HH极化） 图3 飞机模型 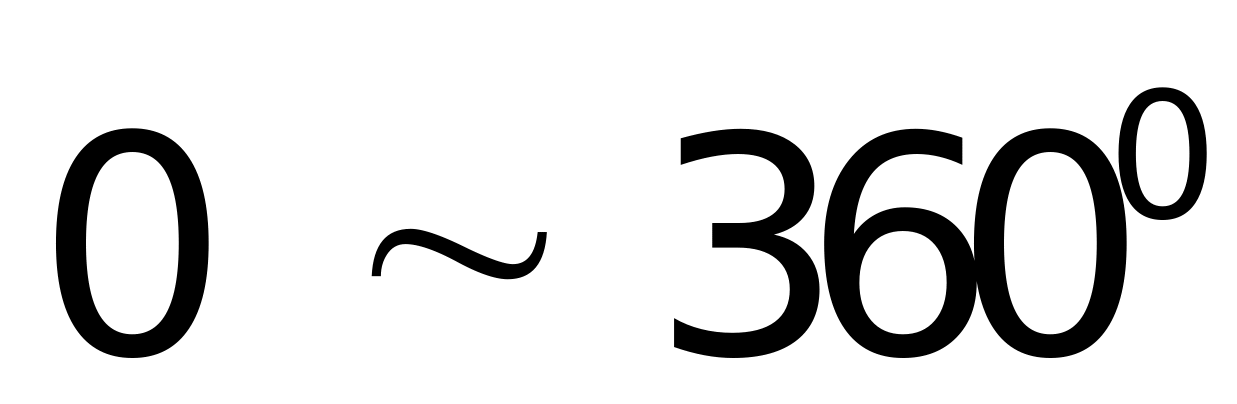RCS强度曲线（VV极化）

进而得到该飞机模型全空域RCS数据以及RCS三维显示，如图（4）、图（5）所示：

图4 飞机模型全空域RCS数据

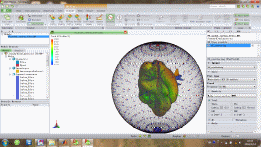
图5 飞机模型全空域RCS三维显示

四、RCS动态数据库建立

对动态雷达目标RCS进行仿真，主要有以下几个步骤:

1.通过实测数据或自定义目标航迹得到目标航迹上一定点数的信息，如航迹上某点相对于雷达的三维坐标数据和当时飞机的姿态角。

2.利用某点在雷达三维坐标中的数据及当时飞机的姿态角进行坐标变换，计算出目标坐标系中雷达所处的位置。

3.利用计算出的目标坐标系中雷达所处位置信息，比对通过FEKO软件建立的静态数据库得出此刻该点对应的RCS值。

4.通过上述方法找出航迹上每点所对应的RCS值，即可实现对目标动态RCS的仿真。仿真流程如图6所示。

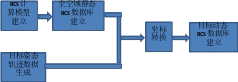
图6 动态RCS仿真流程

（1）雷达坐标系与目标坐标系的定义及相互转换

为了便于描述，先对雷达坐标系及目标坐标系进行定义。

如图（7）所示，雷达坐标系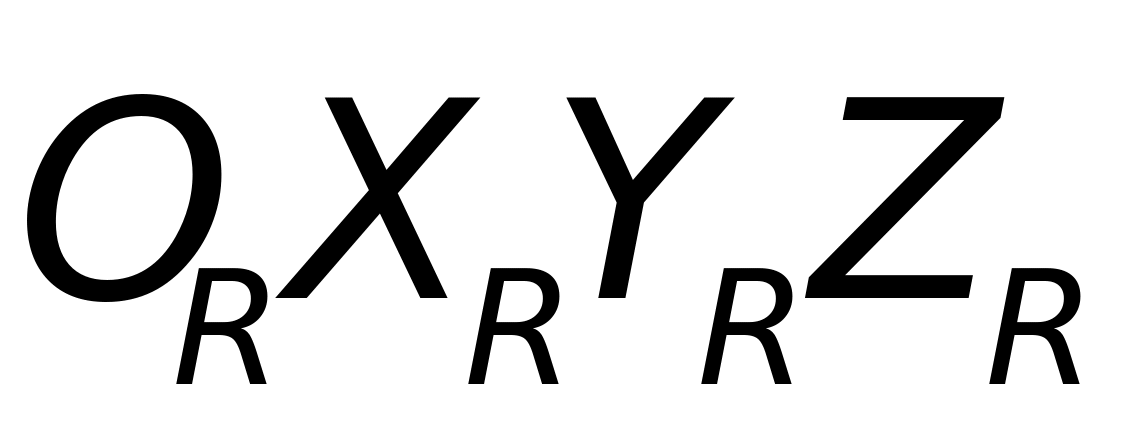 固定于雷达之上，它以雷达所在地为坐标原点（记为 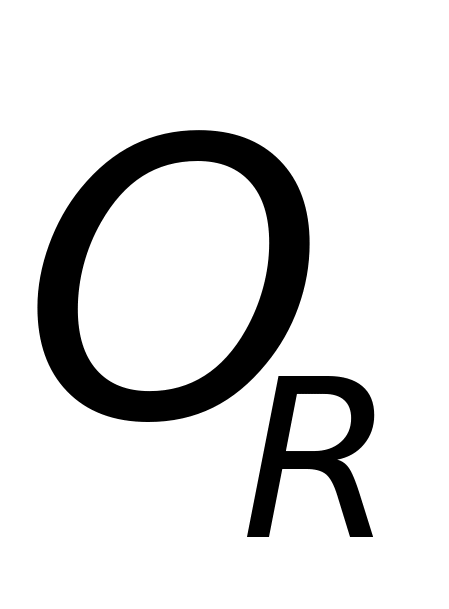）， 轴铅垂向上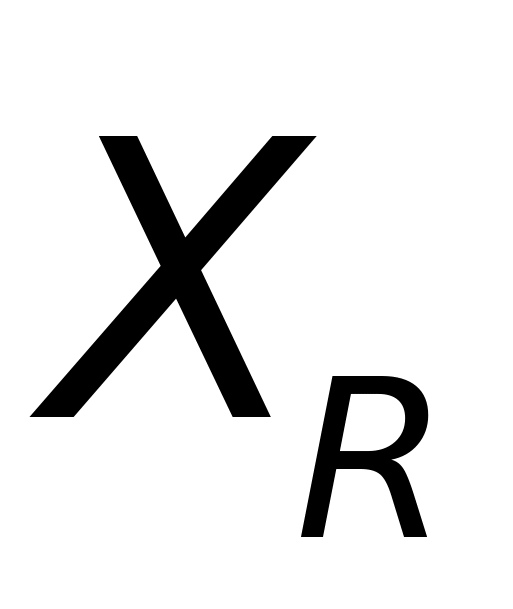， 轴和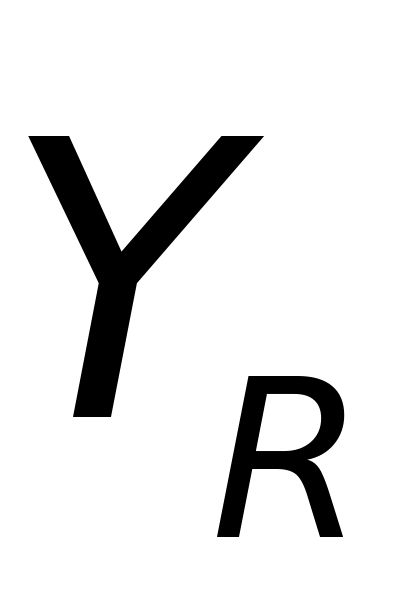 轴位于水平面内，规定Y轴为正东方向，X轴为正北方向。

图7 雷达坐标系

雷达一般以极坐标形式r（t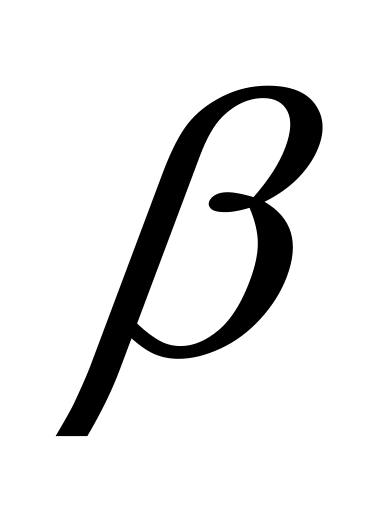）， （t）和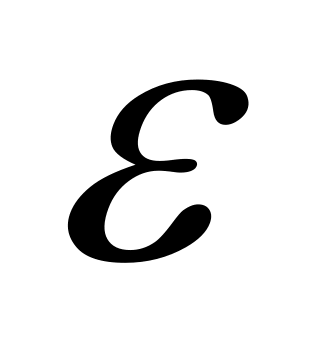 （t）给出目标点迹每一时刻在雷达坐标系中的位置，其中r（t）为雷达原点 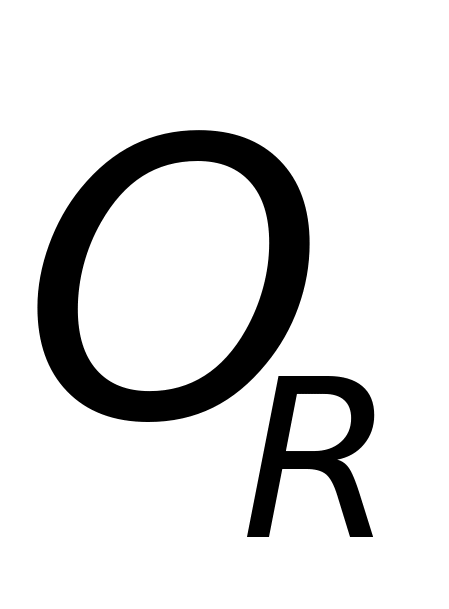至目标中心的距离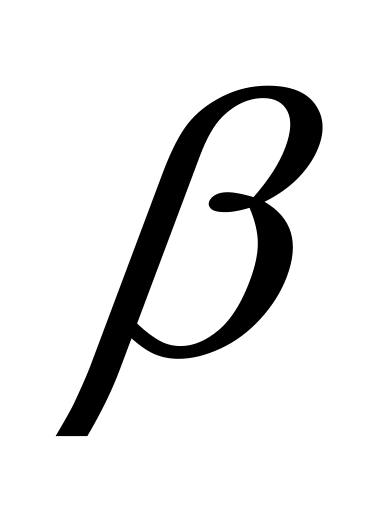， （t）为雷达视线在 平面的投影与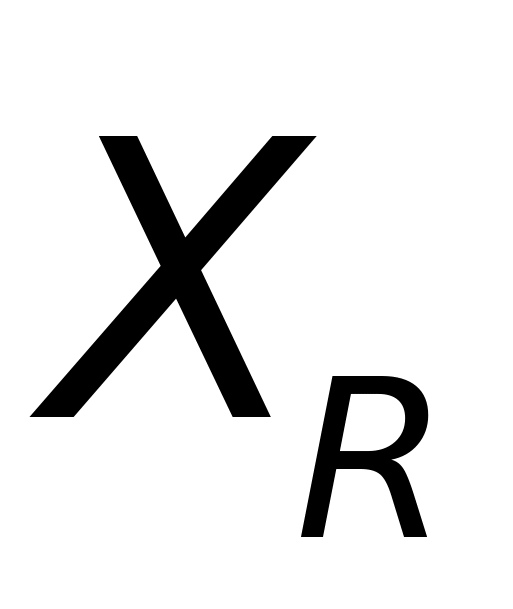 轴的夹角（即目标方位角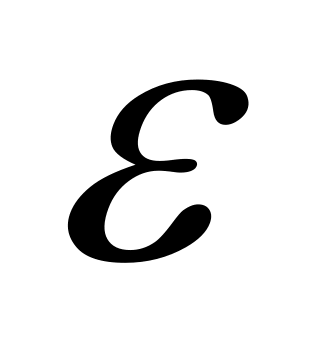）， （t）为雷达视线与 轴的夹角（即目标俯仰角）。变化关系如下

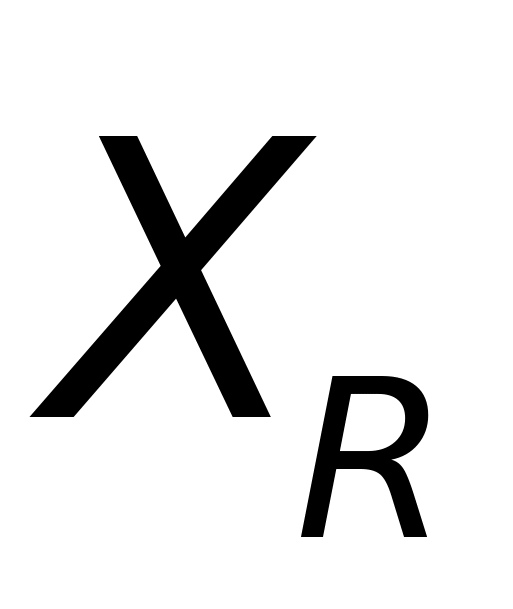（t）= r（t）*sin 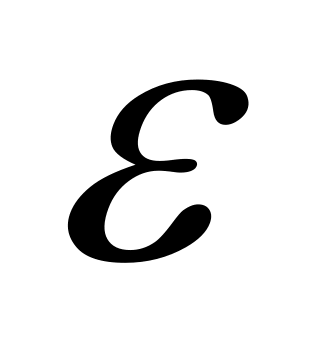（t）*cos 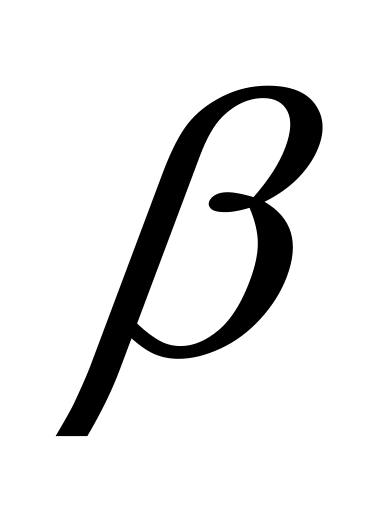（t） （1-8）

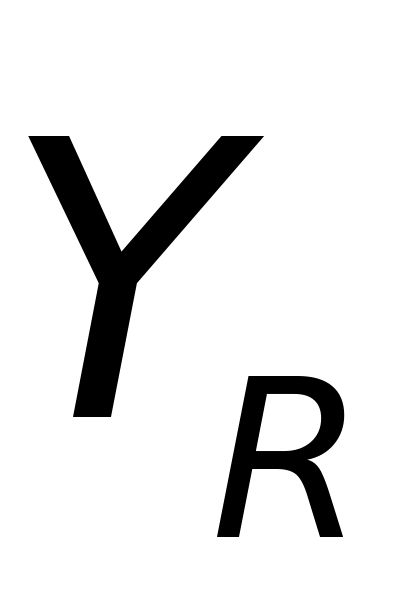(t) = r（t）*sin 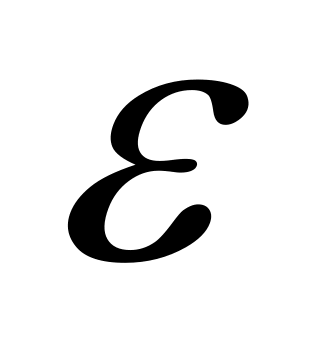（t）*sin 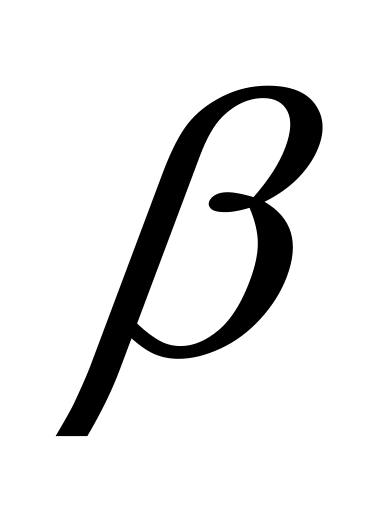（t） （1-9）

(t)= r（t）*cos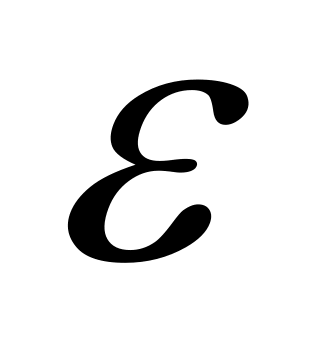 （t） （1-10）

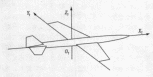
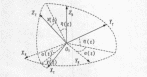
图8目标坐标系 图9坐标系变换

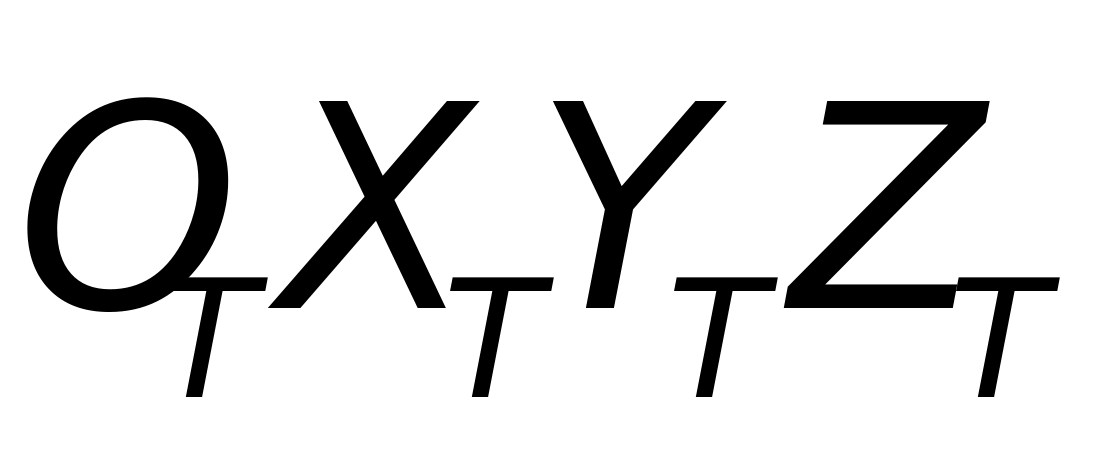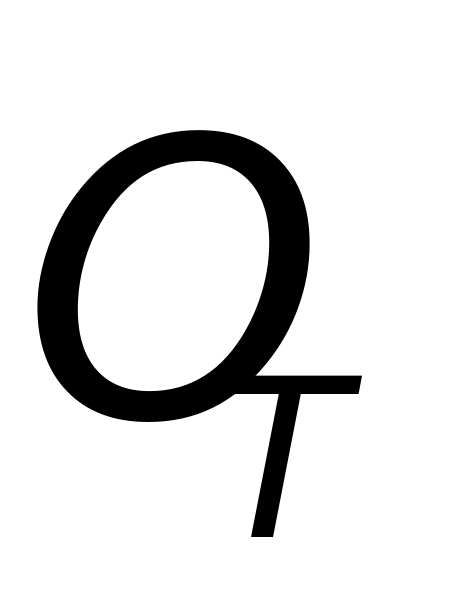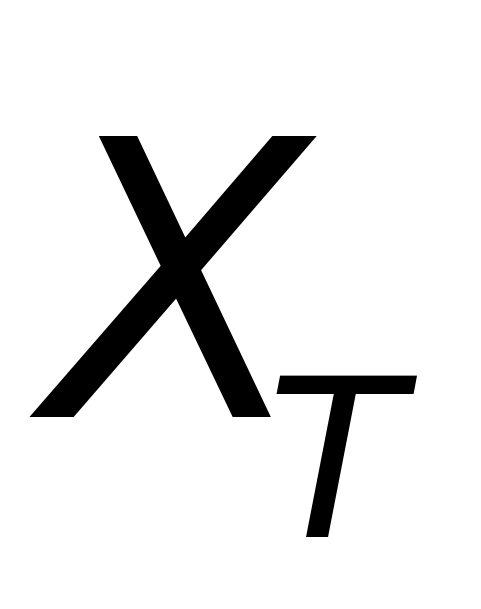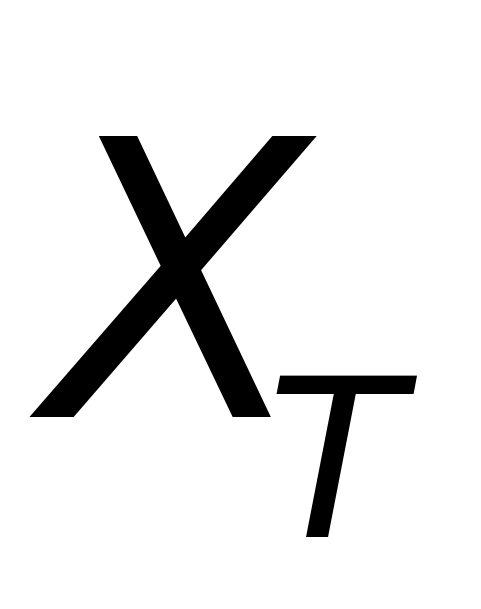如图（8）所示，目标坐标系 固定于目标，它以目标中心为坐标原点（记为 ）， 轴平行于机身轴线指向前方， 轴位于目标对称平面内，垂直于 轴指向上方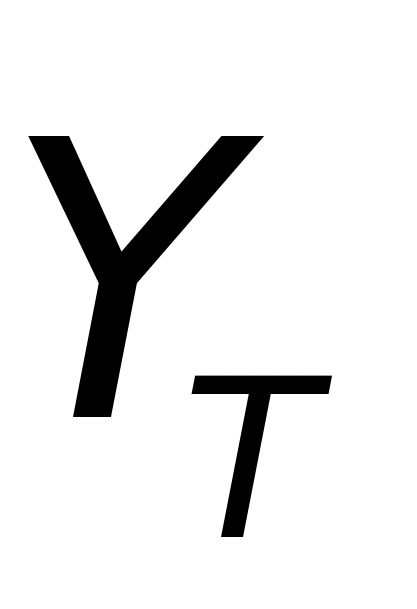， 轴垂直于目标对称平面其指向由右手法则确定。

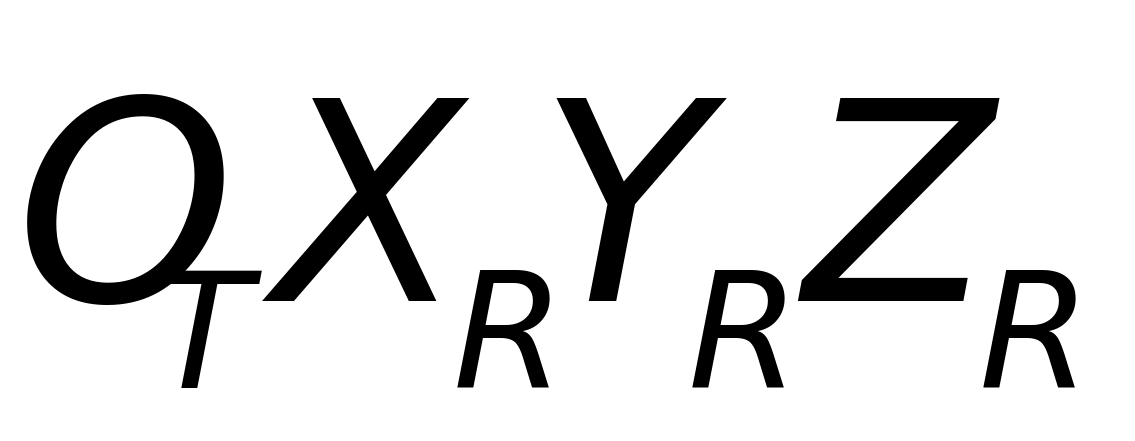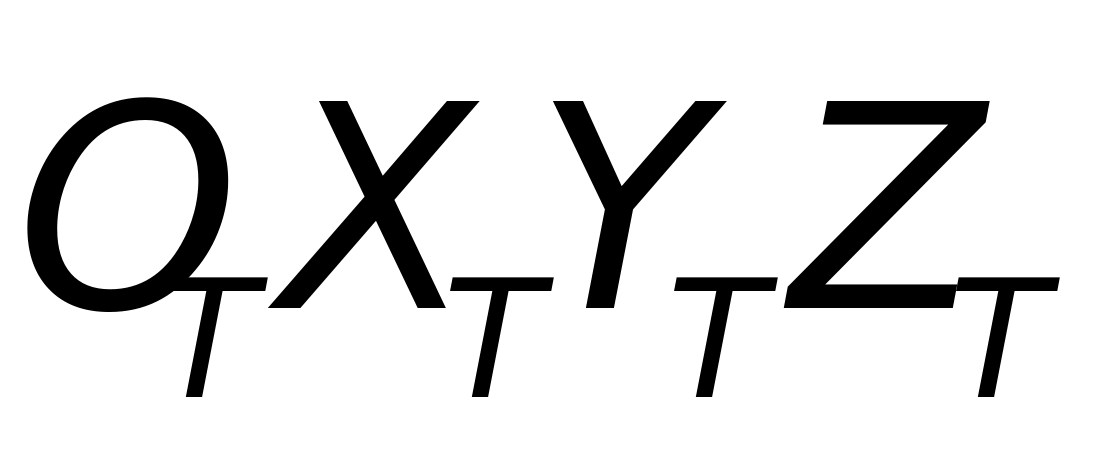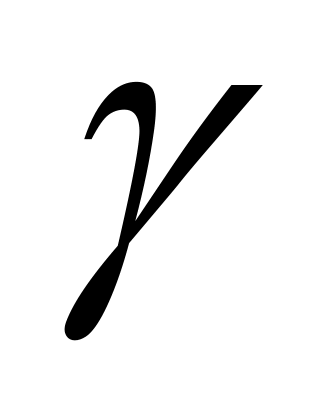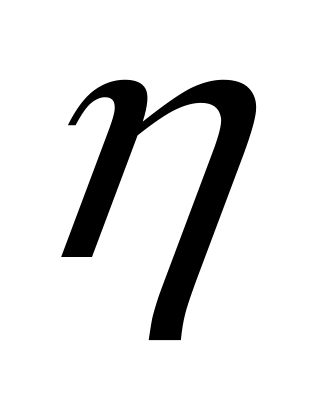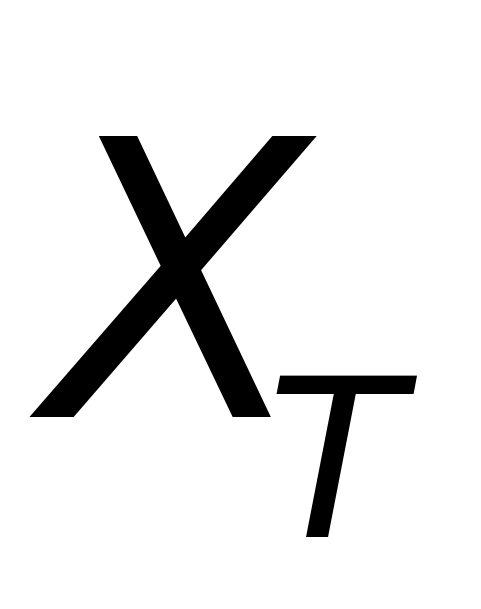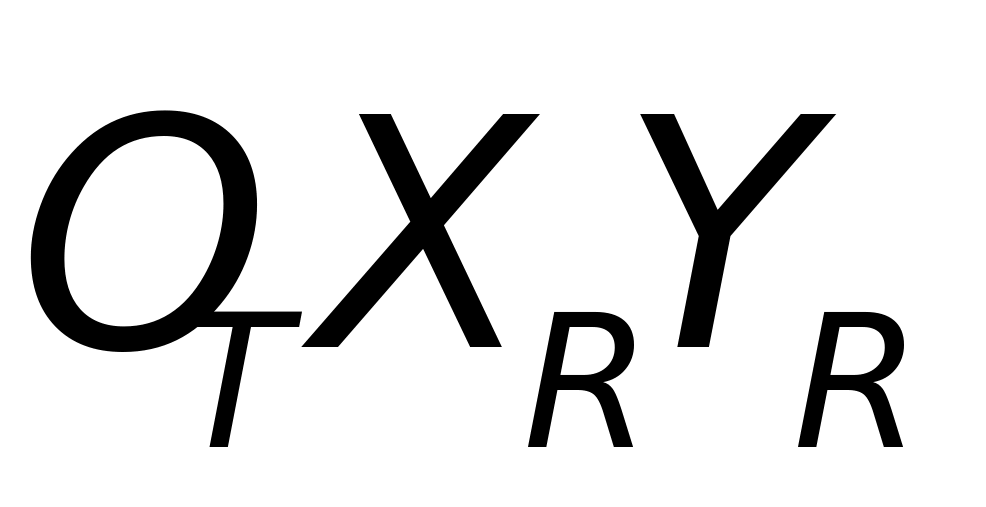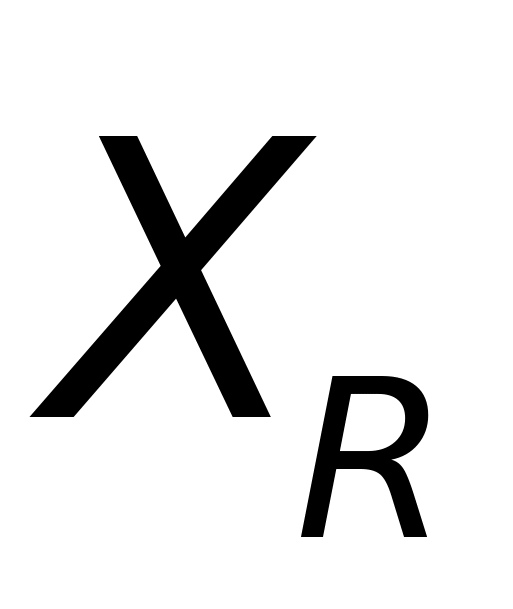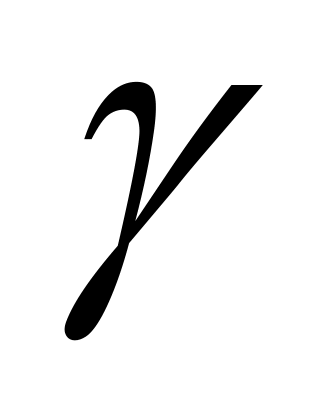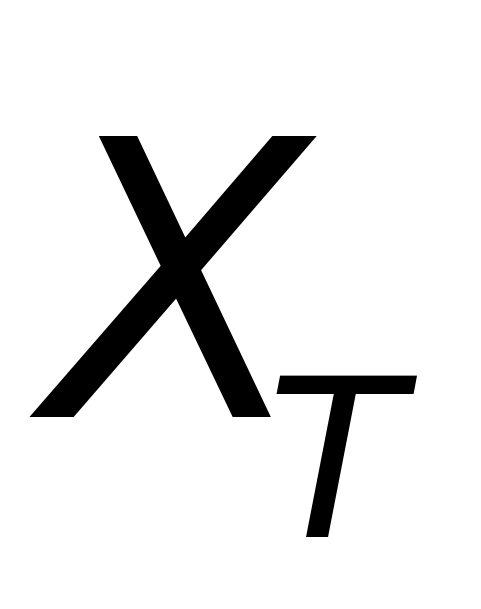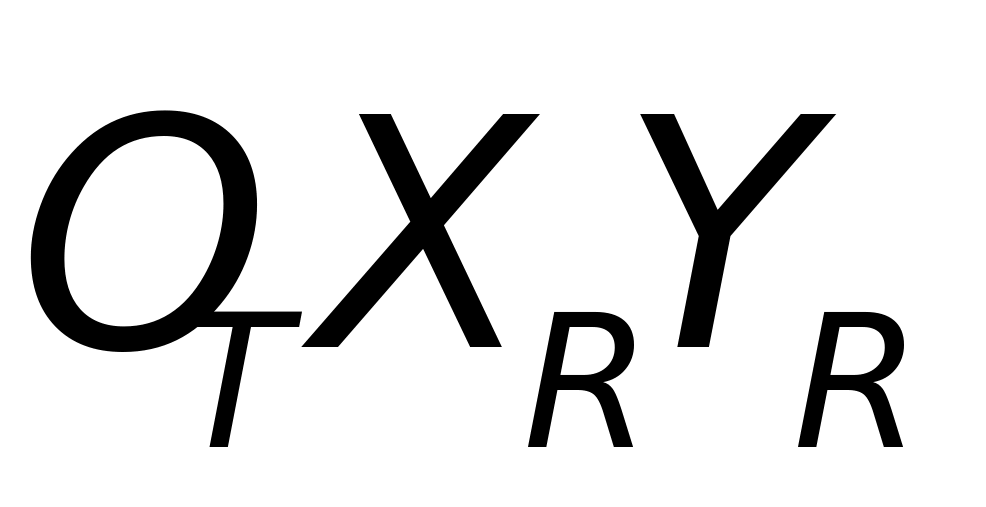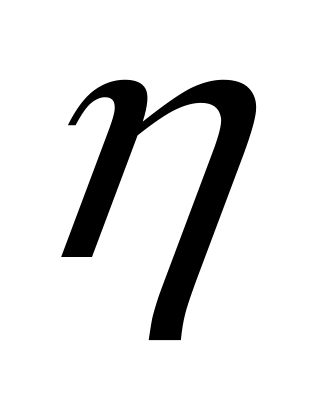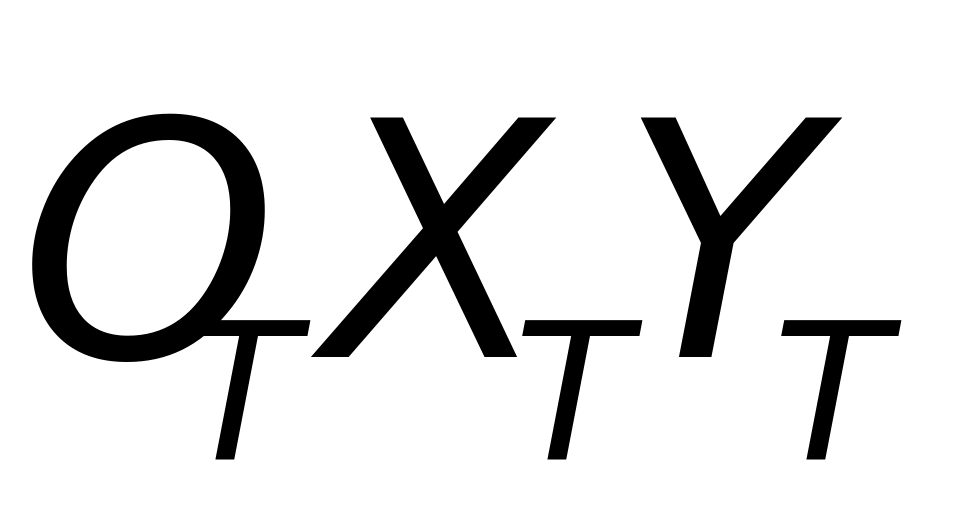如图（9）所示，将雷达坐标系与目标坐标系平移至原点重合。 为雷达坐标系， 为目标坐标系。 （t）、 （t）和 （t）分别为目标偏航、俯仰和滚转角。由这三个欧拉角可以完全确定目标在运动过程中的姿态的变化，其中 （t）为目标机体轴 在 平面上的投影线与轴 之间的夹角， （t）为目标机体轴 与 平面的夹角， （t）为 平面与包含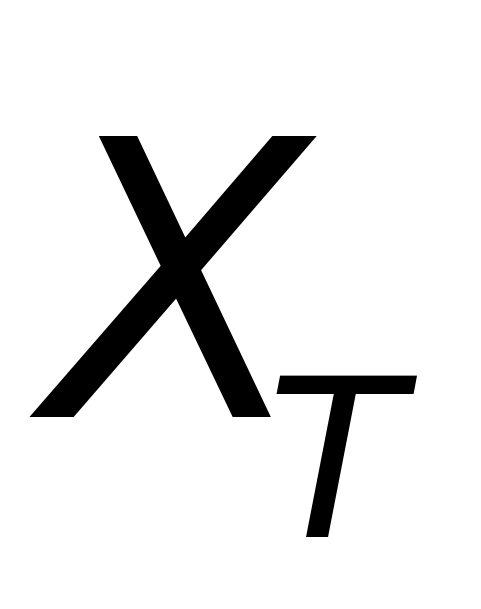 轴的铅垂面之间的夹角。

从雷达坐标系到目标坐标系的变换过程如下：

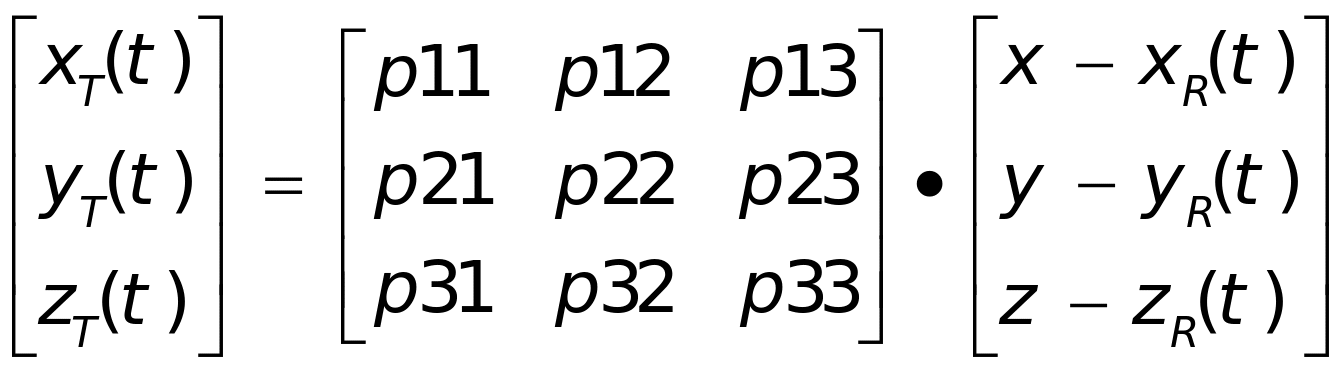=P 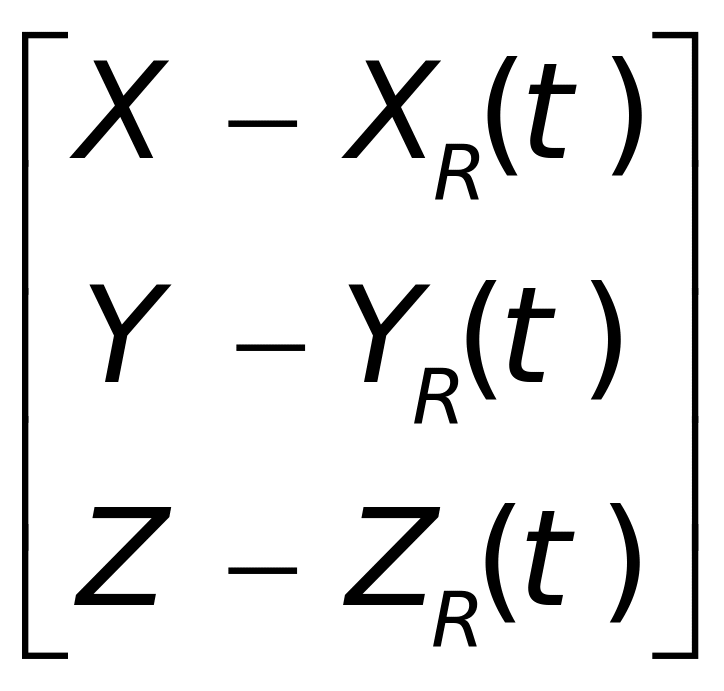（1-11）

式（1-11）中，（x,y,z）为雷达坐标系中任意一点坐标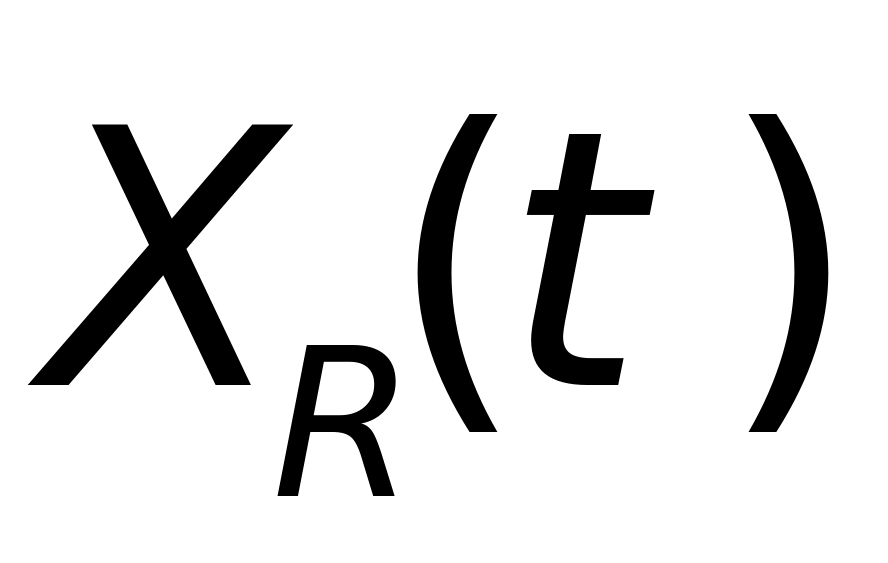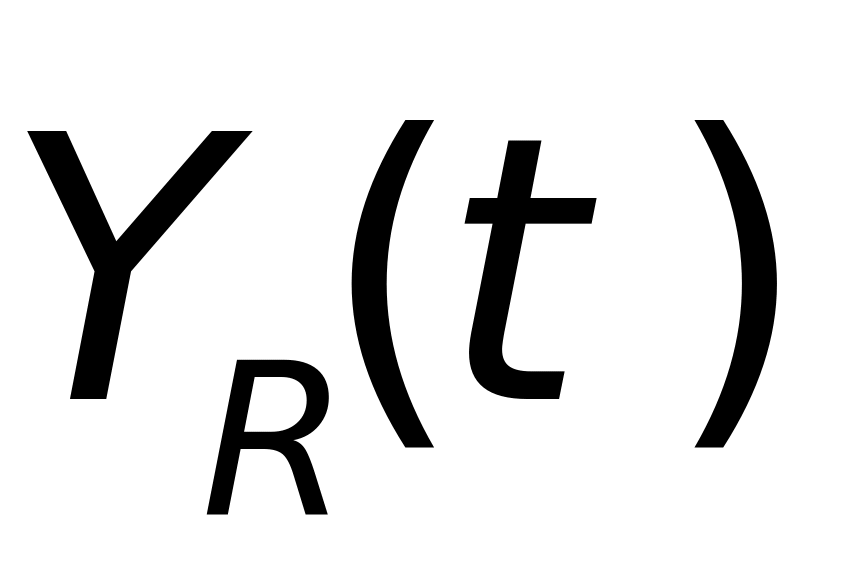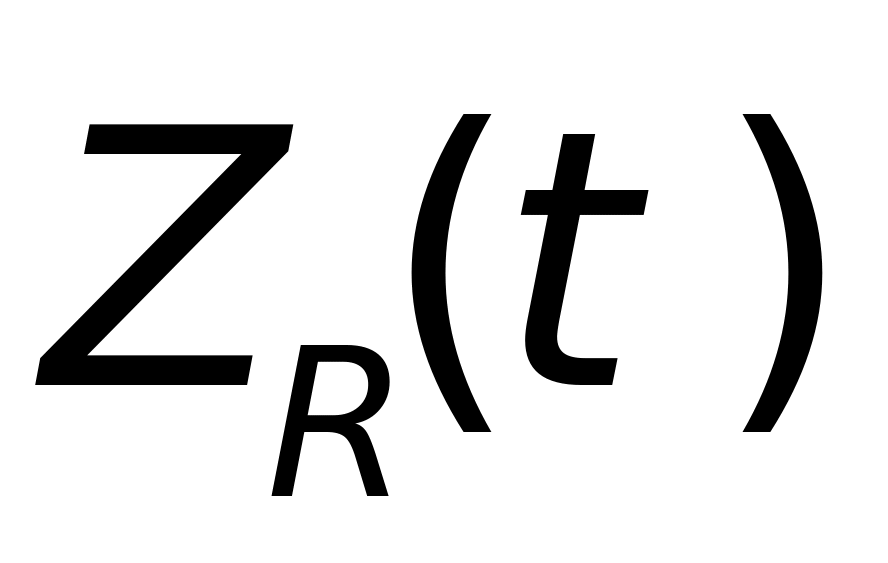，（ ， ， ）为目标点迹在雷达坐标系中的坐标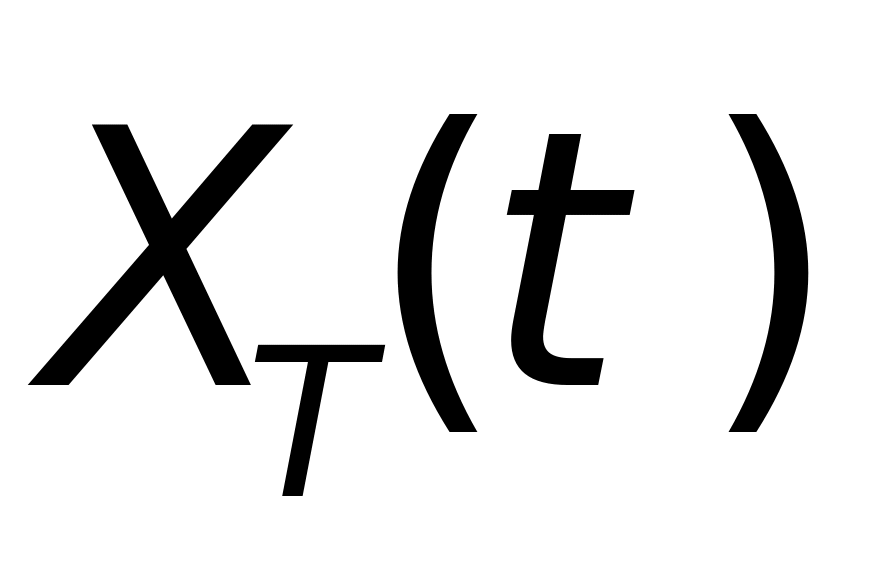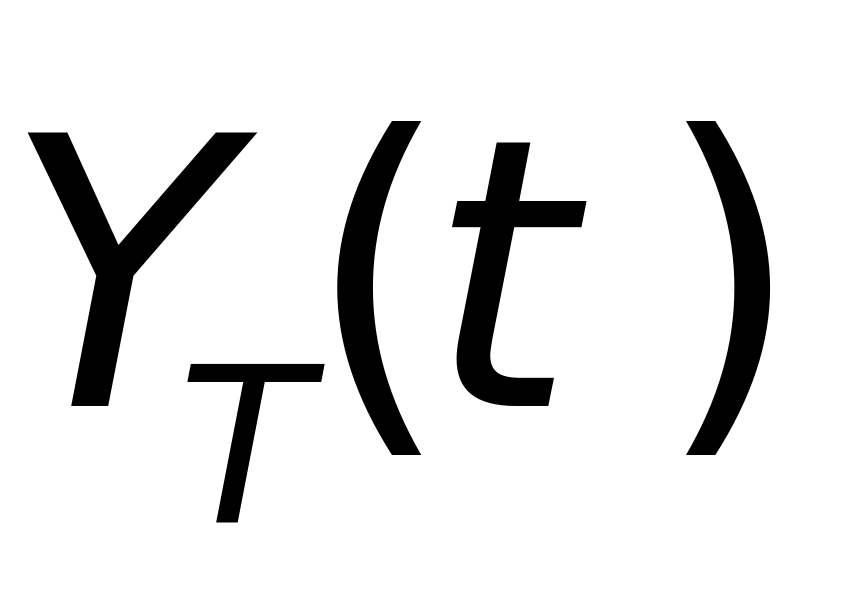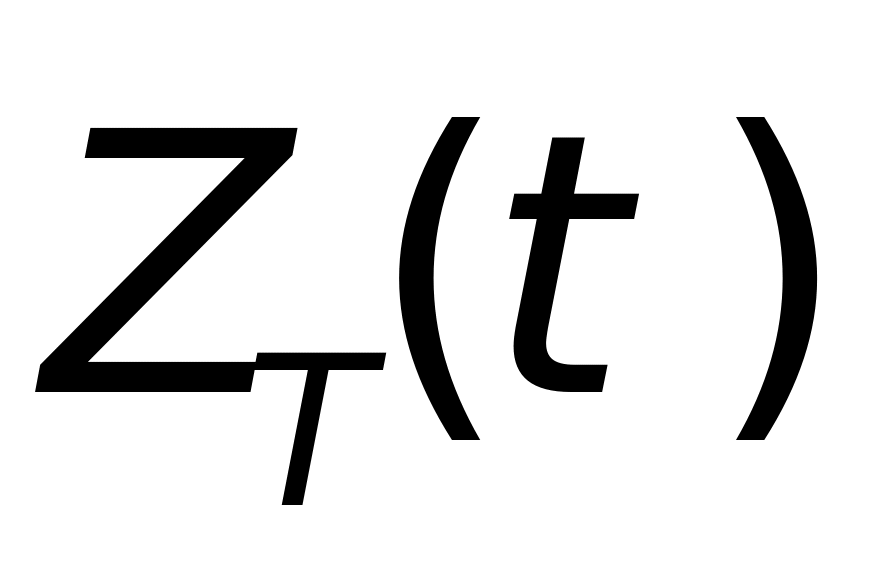，（ ， ， ）为点（x,y,z）在目标坐标系中的坐标。P为从雷达坐标系到目标坐标系的变换矩阵，其分量分别由以下关系式确定。

（1-12）

将雷达坐标（0,0,0）代入可算出雷达位置在目标坐标系中的坐标表示，即

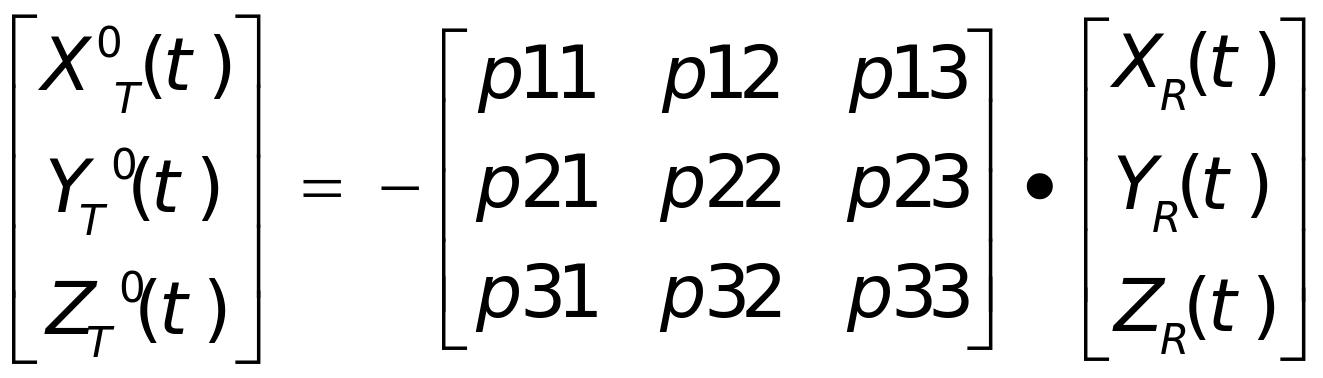（1-13）

式（1-13）中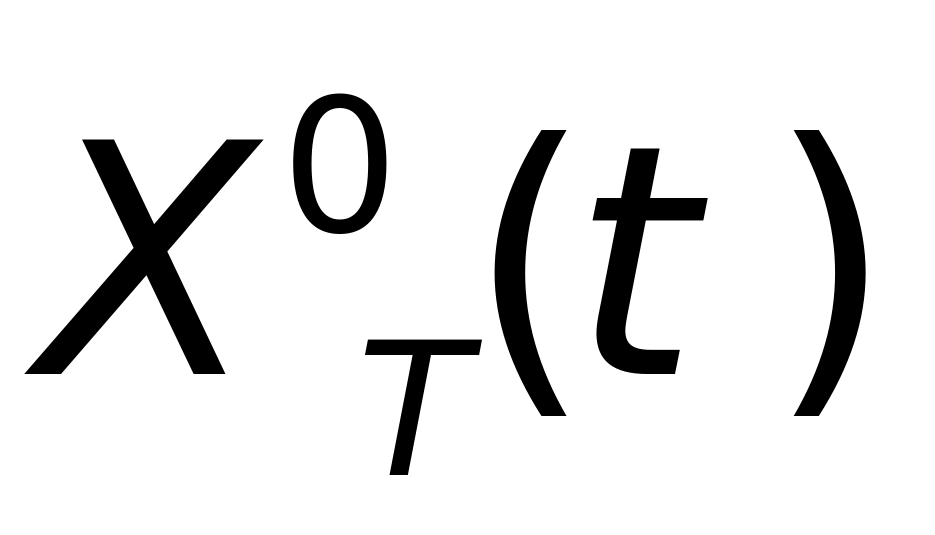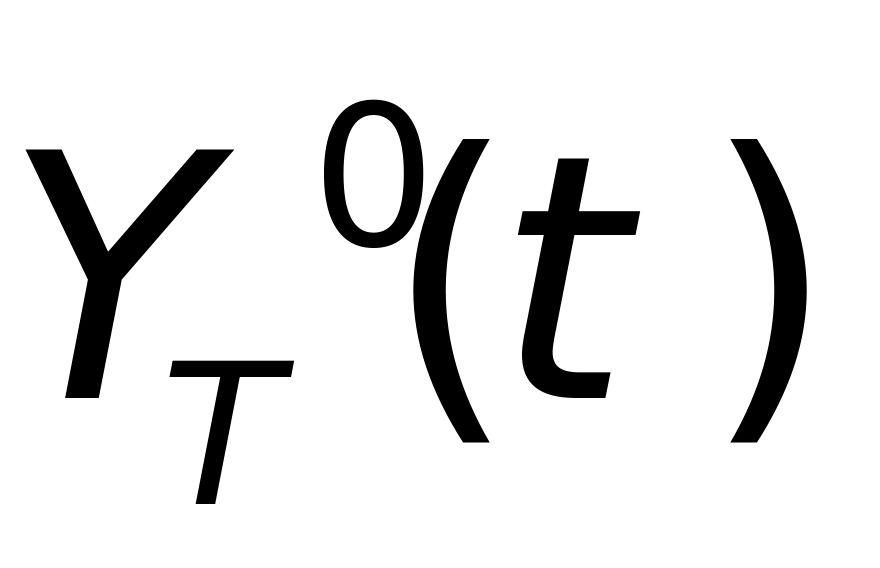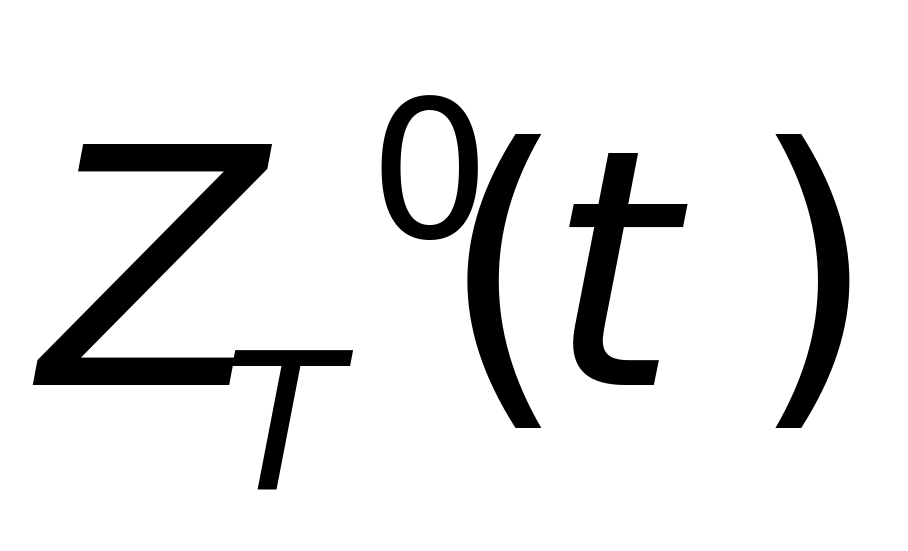，（ ， ， ）为雷达位置在目标直角坐标系中的坐标。将目标相对于雷达运动等价表示为雷达视线在目标坐标系中的姿态角变化，即将直角坐标系表示转换为极坐标表示，即

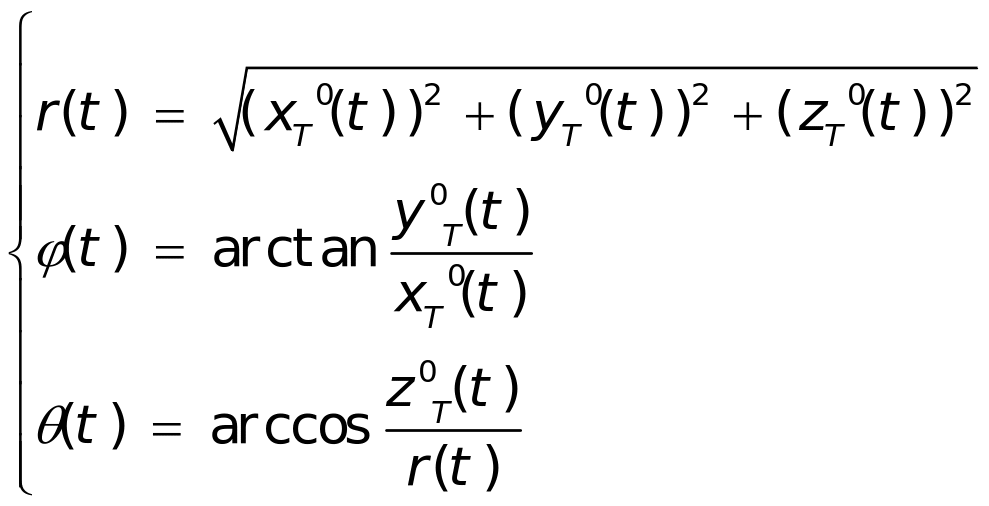（1-14）

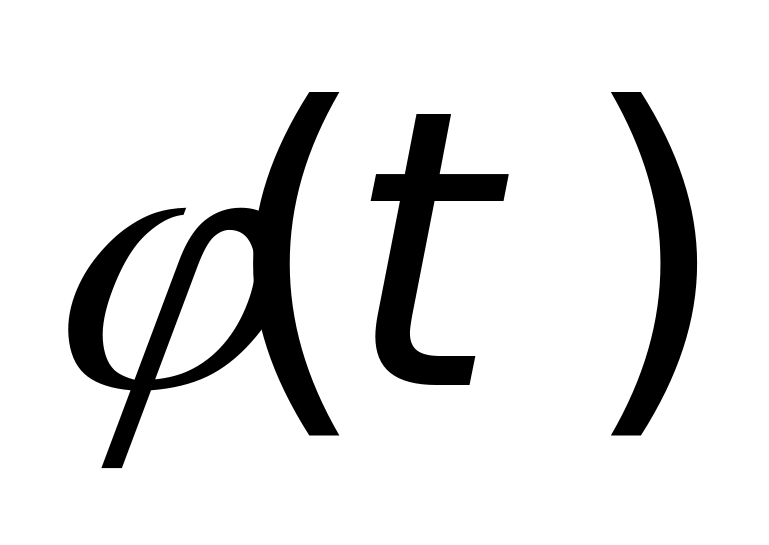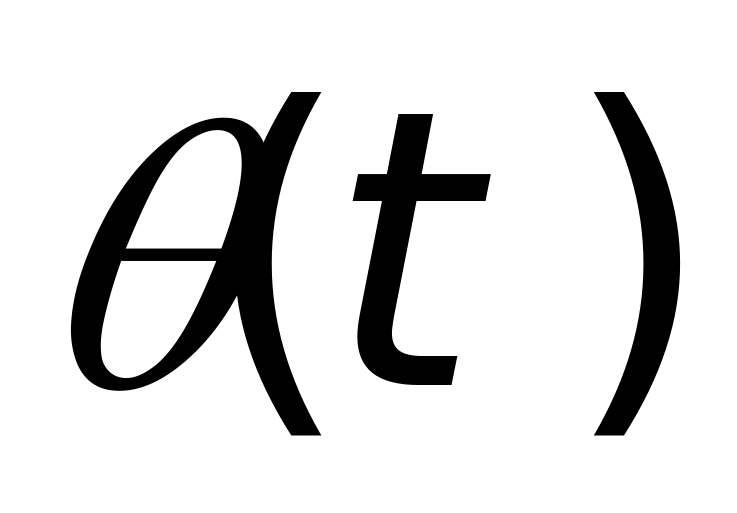， 即为雷达视线在目标坐标系中随时间变化的方位角和俯仰角。在求出每一时刻的 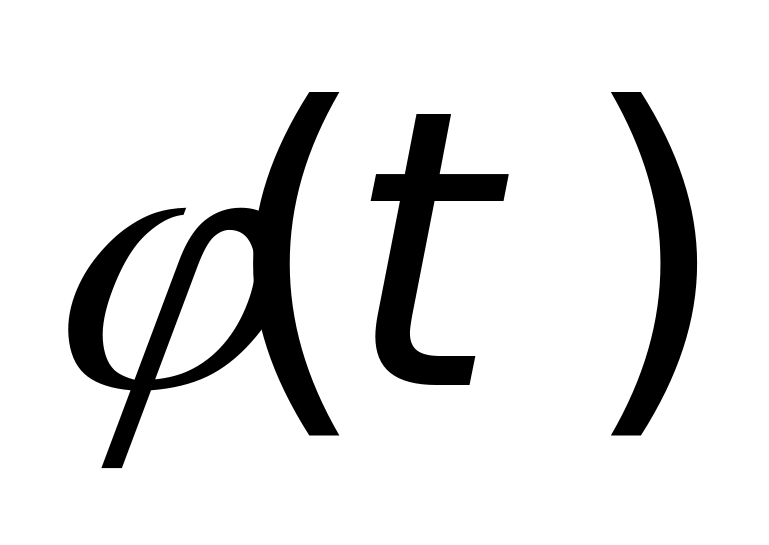和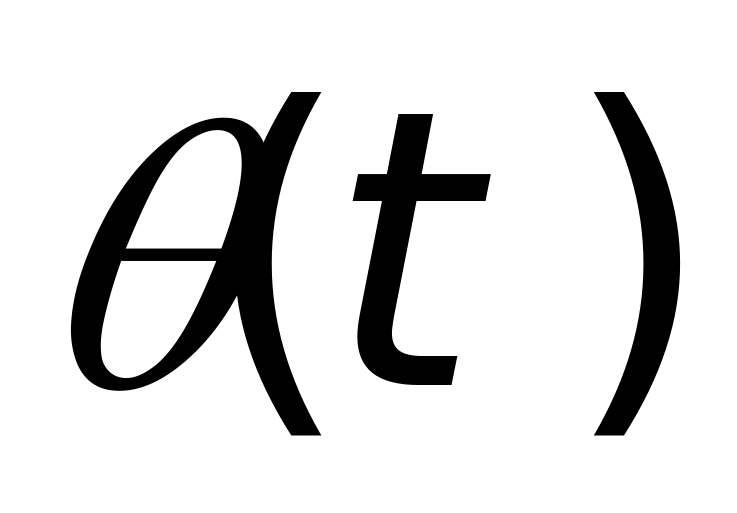 后，即可在目标坐标系中计算出与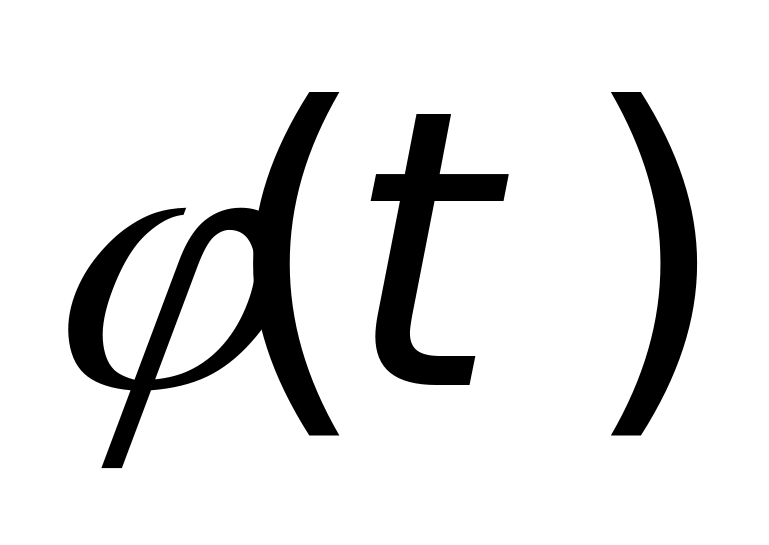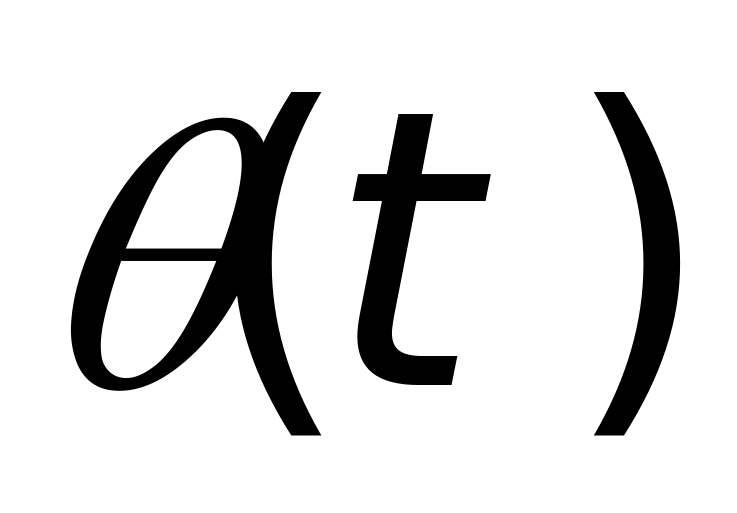（ ， ）相对应的RCS值，也就是在静态数据库中找与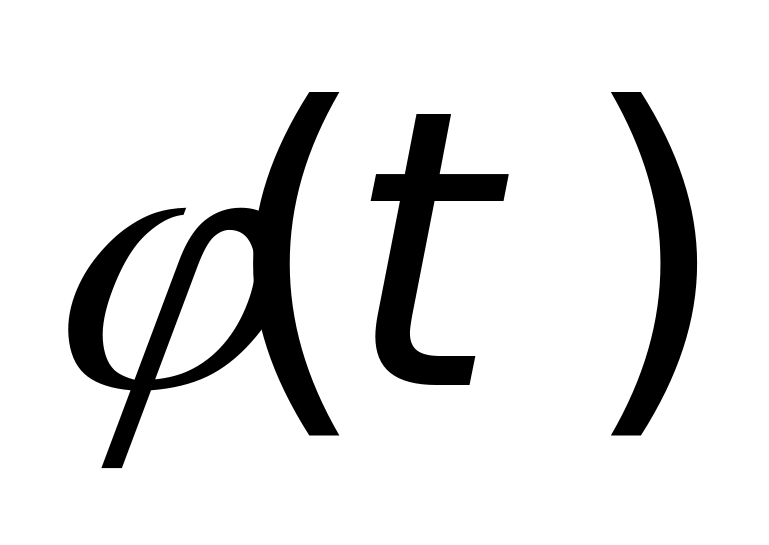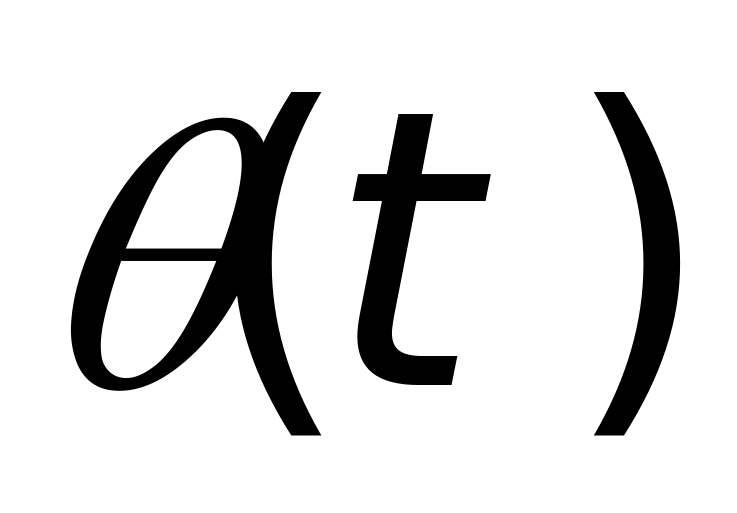（ ， ）相对应的RCS值。

（2）生成目标航迹数据

进行目标动态RCS的仿真一般采用飞机实际测量数据。因条件有限，本文采用仿真产生目标航迹数据。假设一架飞机从坐标为（100,100,10）的位置高度不变匀速直线飞行至（300,100,10）处（坐标单位均为千米）。在整个飞行过程中，该飞机的偏航角、俯仰角和滚转角均为0。从该航线上平均地抽取航线上500个点作为实验对象，利用c#编程得出的试验点如图（10）所示。图中第一、二、三列分别为目标点的（x,y,z）值，第四、五、六列为目标点的偏航角、俯仰角、滚转角。

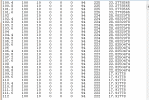
图10 仿真产生的目标航迹数据 图11 仿真产生的目标航迹数据

（3）通过坐标转换计算航线上每点对应的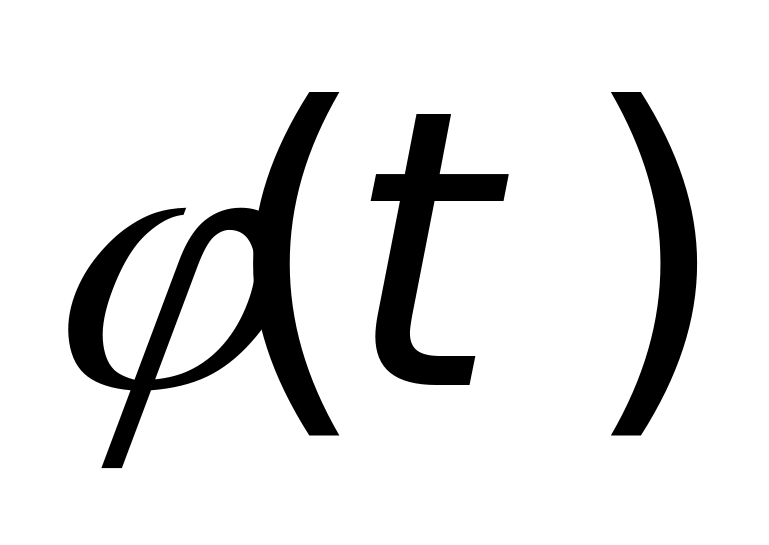 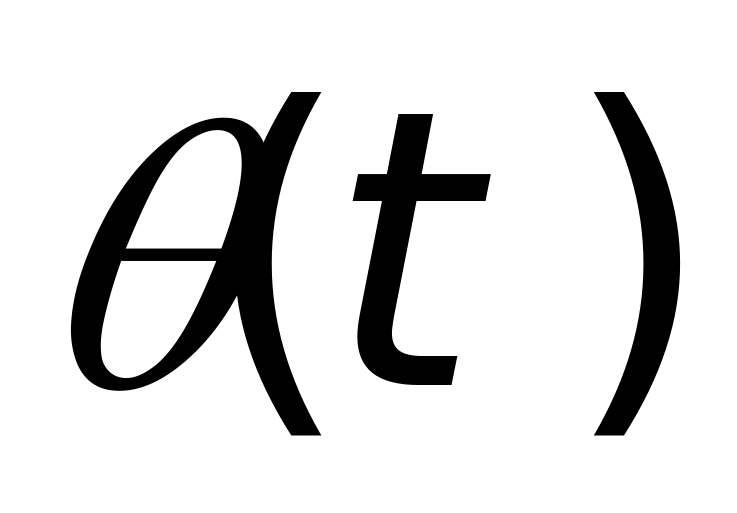， 值，用C#编程，利用坐标转换方程计算出每点对应的 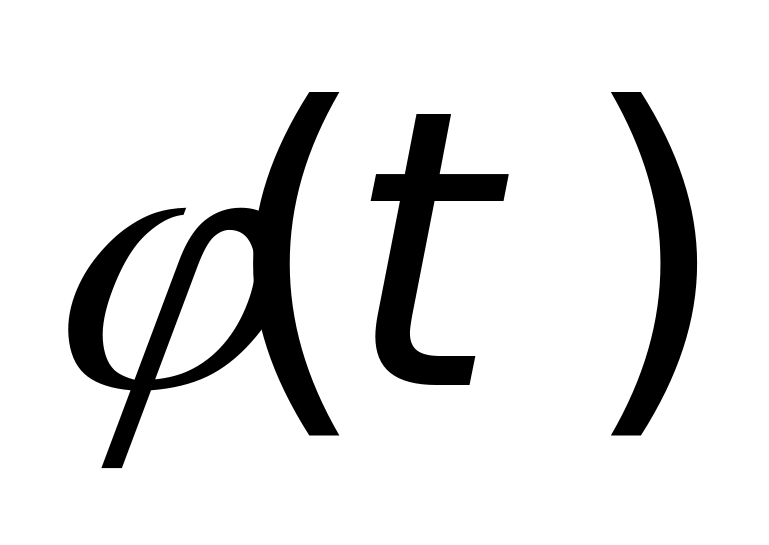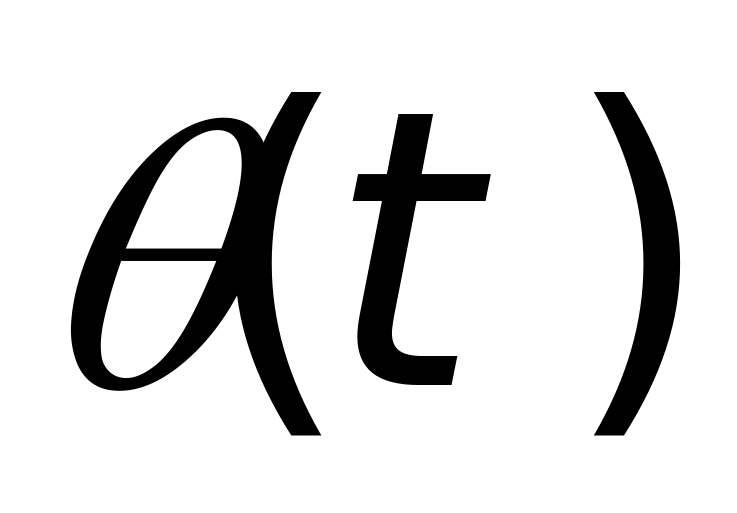， 值，并找出相应的动态RCS序列值。如图（12）所示，其中第七、八列分别为目标点所对应的 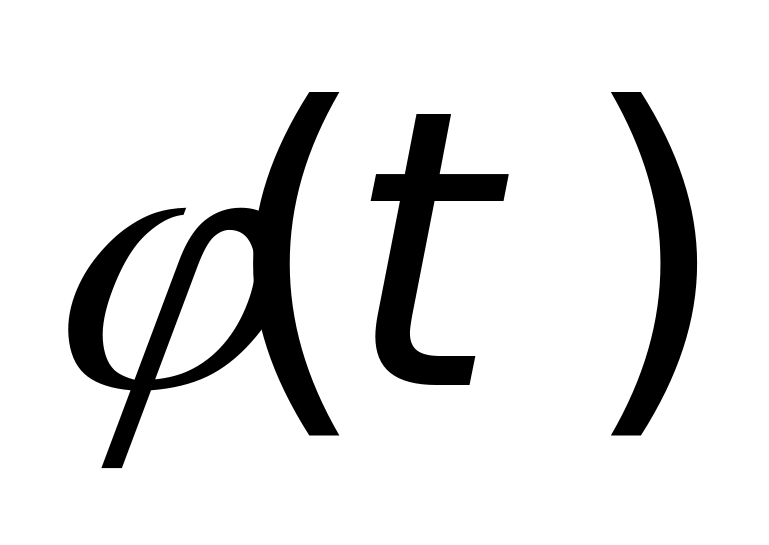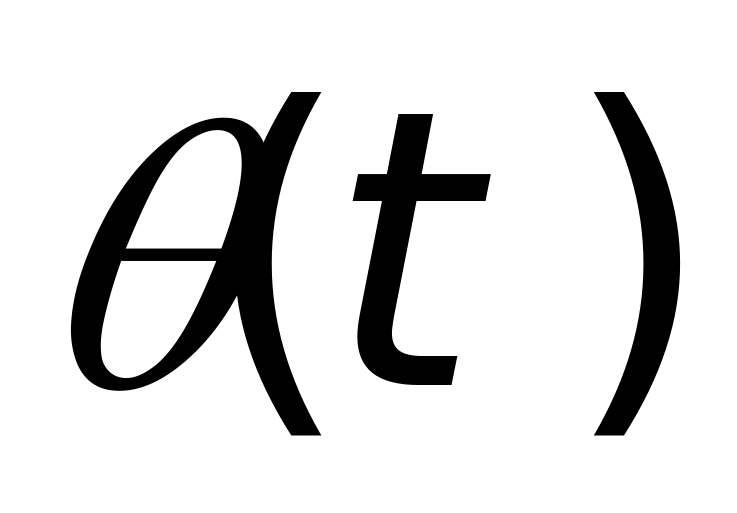， 值，第九列为目标点对应的动态RCS序列值。

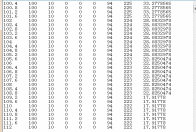
图12目标动态RCS序列

将上述数据通过MATLAB软件仿真便可得到目标动态RCS，如图（13）所示：

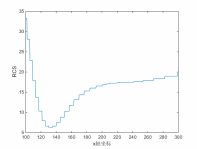
图13 目标动态RCS变化趋势

本文介绍了飞机的精确建模方法，重点讨论了利用全空域静态RCS数据获得飞机动态RCS序列的仿真方法，在实际中雷达目标随机抖动对动态RCS序列有较大影响，由于本文作者水平有限，未能采用目标随机抖动模型进行修正，当飞机采取其他机动时亦可以采用本方法进行仿真。雷达目标的动态RCS序列的快速获得，对研究雷达目标的动态特性具有重要意义。