科研反哺教学实践路径探索——以电路分析课程为例

科研反哺教学实践路径探索——以电路分析课程为例

陈蓓 张希 武花干 徐权

常州大学微电子与控制工程学院 江苏省常州市武进区滆湖中路 21号

【摘要】电路分析课程是电子信息类专业学生的必修基础课程，对电子信息类专业学生的知识体系的构建与核心竞争力的培养具有至关重要的作用。课程内容围绕电路分析方法，全面介绍电路分析的基本概念、基本原理和基本方法，其中基本概念的牢固掌握，是学习好电路分析课程的基石。针对电路分析课程中的基本电路元件这一知识点，结合当今科学研究热点，拓展电路元件基本概念的教学内容，对科研反哺教学的实践路径进行探索。通过将科研与教学相融合，优化教学内容，培养学生创新能力，有效提升电路分析课程的教学质量，为该门课的教学改革模式提供有价值的参考。

1.引言

电路分析课程是电子信息类专业的专业基础课程，课程内容围绕电路分析方法，全面介绍电路分析的基本概念、基本原理和基本方法。主要内容包括电路的基本概念和定律、电阻电路的分析方法、线性电路叠加与等效变换、正弦稳态电路分析、三相电路、频率响应与谐振电路、耦合电感、理想变压器及双口网络、动态电路的时域分析。其中，电路的基本概念作为电路分析课程的第一章内容，是后续课程学习的基础。电阻、电容、电感三大电路基础元件是传统电路分析基本概念章节的核心知识。随着科学研究的深入，《Nature》杂志于2008年报道了惠普公司对TiO₂薄膜的电学特性的研究[1]，发现了一种新的电路元件，命名为忆阻，被称为第四种电路元件，这一概念拓展了基础电路元件的范围，为基础电路元件的应用，提供了更多的可能。本文以电路分析课程中的基础电路元件为例，探讨一种科研反哺教学的实践路径，通过科研与教学融合，提高课程的教学质量，培养学生们的创新精神，为该门课程的教学改革模式提供参考。

2.三大基础电路元件及忆阻

电阻元件是电路中用的最多的元件，根据德国物理学家欧姆在1926年发现的欧姆定律，给出了定义：一个两端元件在任意时刻，其两端电压与流过的电流的关系可由电流‒电压平面上的一条曲线（伏安特性曲线）确定，则称这一元件为电阻元件，简称电阻。如果该曲线是一条经过原点的直线，则称该电阻为线性电阻。在一个线性电阻两端施加电压u，通过电流表检测得到流过电阻的电流为i，可以得出如图1(a)所示的线性电阻元件的伏安特性曲线，该曲线是一条通过原点的直线，直线的斜率即为元件的电阻R。由欧姆定律，可以得到，元件的电阻为

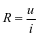
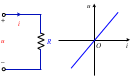
图1 线性电阻元件及其伏安特性曲线

如果元件上的电压‒电流曲线不是一条直线，而是一条通过原点的曲线，那么这种电阻称为非线性电阻。不论线性电阻还是非线性电阻，电阻元件的代数关系都可以表示为

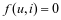
即为电压和电流的关系，这一表达式称为电阻元件的本构关系。

电容元件是从实际电容器抽象得到的电路模型，是表现电容器容纳电荷本领的物理量。电容元件的定义为：某个二端元件在任意时刻的电荷量q和电压u之间存在代数关系

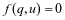
则此元件可称为电容元件。当q‒u平面上的这条特性曲线是通过原点的直线时，称为线性电容，否则称为非线性电容，如图2所示。对于线性时不变电容，在任意时刻的电容值，可以表示为

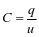
C是一个与q、u无关的正实常数，其数值等于单位电压施加在电容两端时，电容元件存储的电荷量，因此电容C代表了电容元件存储电荷的能力。

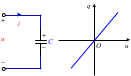
图2 线性时不变电容元件及其特性曲线

电感元件是从实际电感器抽象出来的电路模型，其定义为：某个二端元件在任一时刻的磁链ψ和电流i之间存在代数关系

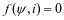
此元件可称为电感元件。这一关系可由ψ‒i平面上的一条特性曲线确定，当这一特性曲线是通过原点的直线时，称为线性电感，否则称为非线性电感，如图3所示。对于线性时不变电感，在任意时刻的电感值，可以表示为

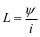
L是一个与ψ、i无关的正实常数，其数值等于单位电流流过电感时，电感元件所产生的磁链，因此电感L代表了电感元件存储磁场的能力。

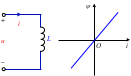
图4 线性时不变电感元件及其特性曲线

根据电流的定义，电流是单位时间流过某一截面的电荷量，因此可以得出

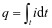
根据电磁感应定律，电感电压等于磁通ψ的变化率，当电压的参考方向与磁链的参考方向相关联时，即符合右手螺旋定则，可以得出

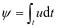
根据电阻、电容、电感三个元件的本构关系，我们可以得出如图4所示电路元件关系图。如图4所示，四个电学基本量为电流i、电压u、电荷q和磁通ψ。其中电阻构建了电压与电流之间的关系，电容构建了电荷与电压之间的关系，电感构建了磁通和电流之间的关系。为了形成完备的网络，缺失了磁通与电荷之间的关系表达。那么是否存在描述磁通与电荷关系的元件呢？

图4 电学基本变量关系图

1971年，加州伯克利分校蔡少棠（Leon O. Chua）教授，从理论上预测了描述磁通与电荷关系的元件的存在，并将之命名为记忆电阻器（简称忆阻器）[2]。2008年，惠普公司的Strukov等人通过对TiO

₂薄膜进行氧空位掺杂，成功发现了第一个物理实现的忆阻器[1]。在忆阻器两端施加电压，测量通过的电流，得出如图5所示的电压-电流曲线。在不同频率下，曲线都表现为通过原点的捏滞回线。随着频率的增大，捏滞回线的旁瓣面积不断减小，当频率增大到某一值后，捏滞回线收缩为一条直线。这一奇特的电压-电流曲线，我们通俗地称之为“8字线”。忆阻器的成功发现与忆阻理论的提出，使得电学基本变量构成了完备体系，因此，忆阻被称为第四种电路元件。

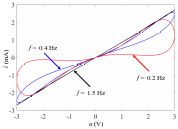
图5 忆阻器特性曲线

3. 典型应用

在人类的大脑中，神经元帮助我们完成学习、阅读、写作、记忆以及情感。神经元是人类的基石，允许大脑的许多复杂过程的发生。二神经元网络如图6所示，每个神经元都有一个细胞体，通过制造蛋白质和能量使细胞保持活力。细胞核也充当细胞的大脑，因为它能处理所有传入的信息并告诉神经元做什么。在神经元中，长轴突和树突分支出来以发送和接收来自其他细胞的信息。在轴突的末端，有一些称为轴突末梢的结构，通过接触其他神经元的树突，形成称为突触的专门连接。当神经元彼此交谈时，它们会发送电化学信息，这些信息可能导致下一个神经元向其轴突发射动作信号。以这种方式，信号可以沿着整个神经元链发送。为了加速信号传导，许多神经元被称为髓鞘的脂肪层隔离，类似于导线绝缘的方式。忆阻器表现出的可编程性和非挥发性，称为模拟突触可塑性和神经递质储存囊泡行为的有利元件。突触可塑性，是通过动作电位控制神经递质的释放，从而改变突触权重，这一行为恰巧与忆阻的非挥发性具有可比拟性。

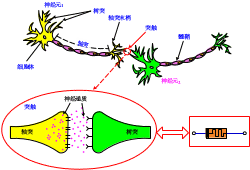
图6 二神经元网络结构图

科学家们通过在模拟电路中引入忆阻器，搭建的忆阻基神经电路可以成功模仿电生理信号的短期增强和长期强化，这是学习和记忆功能得以实现的基础。忆阻基神经形态电路的部分电路如图7所示，电路中的元件包括电阻、电容、MOS管、二极管、运放，以及忆阻器[3]。这一个简单的模拟电路，可以成功模拟突触可塑性。忆阻基神经神态电路的出现，给神经损伤患者的康复带来了福音。

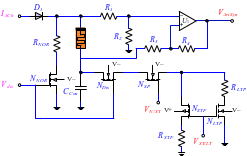
图7 忆阻基神经元电路的部分电路图

5.总结

电路分析课程是电类学生的必修基础课程，具有很强的理论性与应用性，对后续专业课程的学习产生重要影响。通过科研反哺教学的模式，以基本电路单元知识点为例，将科研成果和学科前沿进展融入教学环节，实现教学和科研的良性互动，充分拓展学生思维，提高学生热情，不断提高教学质量。

参考文献

[1] D.B. Strukov, G.S. Snider, D.R. Stewart, et al. The missing memristor found. Nature, 2008, 453(7191): 80-83.

[2] L. Chua. Memristor-The missing circuit element. IEEE Transactions on Circuit Theory, 1971, 18(5): 507-519.

[3] Z.I. Mannan, S.P. Adhikari, C. Yang, et al. Memristive imitation of synaptic transmission and plasticity. IEEE Transactions on Neural and Learning System, 2019, 30(11): 3458-3470.

常州大学教育教学研究课题，项目号：GJY2020078，GJY2020064 ，2019XSJY03，GJY2020059。