山东协和学院 山东济南 250109
摘要:本文针对生产企业原材料的订购与运输问题,综合考虑供应商的交货率、平均供订比、供货频率,建立基于TOPSIS的最优决策评价模型,用于解决供应商的选择问题。通过对附件1中的订货量与供货量数据进行分析,选取了交货率、订供比、交货频率三个供货特征作为评价指标并进行量化分析,建立了基于TOPSIS的最优决策评价模型,借助MATLAB软件对该模型进行编程求解,得到综合得分排名表并以此确定50家最重要的供货商。
关键词:供货特征 量化分析 决策评价模型
现有某建筑和装饰板材企业需要采购木质纤维材料和其他植物素纤维材料,主要有A、B、C三类材料。该企业每年安排48周生产计划,其中24周的采购和转运必须提前制定以保证企业的正常运行。企业每周的产能固定为2.82万立方米,每立方米需要A或B或C类材料来进行加工,除此以外,A类与B类原材料的采购单价均贵于C类且分别比C类原材料高20%和10%。与此同时,为了防止供应商供应不足影响每周的生产计划,因此企业总是保证库存量大于或等于两周生产所需。原材料的采购成本将会直接影响企业的收益,供应商与转运商的选取也会通过影响存储费用和材料损耗间接的影响企业收益,在每类材料价格都相同的情况下,不同材料的采购数量与供应商和转运商的选取将成为影响收益的重要因素。
题目中附件1为企业在5年内的订货量与供应商供货量的数据。根据附件1对402家供货商的供货特征进行量化分析并建立保证企业生产的数学模型,以此确定50家供应商。
要量化分析供应商的供货特征并建立能够保障生产重要性的模型,确定50家最为重要的供应商。我们首先要对附件1中的数据进行预处理,然后对数据进行可视化分析,综合分析企业订货量与供应商供货量的数据特征,选取合适的评价指标并建立评价指标体系,最后在此基础上建立合理的评价决策模型,并以此来确定50家供应商。
1.忽略企业每周订购原材料的剩余数量对库存的影响。
2.假设企业在第一周开始时没有库存,忽略在第一周开始前的储存费用。
符号 | 含义 | 单位 |
| 交货率 | 无量纲 |
| 供应商交货总次数 | 次 |
| 企业订货总次数 | 次 |
| 平均供定比 | 无量纲 |
| 供应商 | 无量纲 |
| 时刻周 | 周 |
| 供货频率 | 无量纲 |
| 数据正向化转换值 | 无量纲 |
| 评价得分 |
1.供货特征的量化分析
数据预处理
在实际生活中,会发生由于某些原因导致供应商未在规定时间内提供原材料的情况,于是,我们对供应商交货准时率[1]进行分析,借助Python软件对企业订货量和供应商的供货量进行逻辑判断,通过求解分析发现订货量为零,供货量大于零的情况全部为False,即当周订货当周供货,不存在供应商供货不准时问题。
供货特征指标的确定
通过查阅有关供应商选择的文献[2]了解到供应商的产品质量、产品延时率、供货能力等均是选择供应商的重要参考指标,但是本题未直接体现产品质量,延误率等问题,我们综合考虑数据特征与社会实际情况,最终选取交货率、平均供订比、供货频率三个指标作为量化分析供应商供货特征的指标。
交货率:交货率是供应商交货的总次数占企业订货的总次数的百分比。即:
 。
。
平均供订比: 平均供订比是第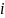 家供应商在240周时间内供订比之和与企业订货总次数的比值。即:
家供应商在240周时间内供订比之和与企业订货总次数的比值。即:
 。
。
供货频率:供货频率是每家供应商在240周时间内发货总次数与240周次的比值。即:
 。
。
2.基于TOPSIS的决策评价模型的建立
通过查阅文献[3]了解到:供应商的选择问题显著影响着企业的生产经营,想要科学决策选择供应商,企业需要建立评价指标体系综合考虑供应商的优缺点,选取合适的供应商。于是,我们决定建立基于TOPSIS的决策评价模型。对于供应商的选择,主要是企业人员的客观评价,因此我们借助层次分析法确定评价指标的权重
[4],给出评判矩阵,分析供应商的供货特征。
中间型指标平均供订比正向化
 ,
,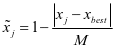 ,
,
其中,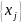 为中间型指标序列,
为中间型指标序列, 为最佳数值,
为最佳数值,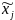 为计算的转换值。
为计算的转换值。
层次分析法确定权重
为了降低较强主观性带来的偏差,分别采用算术平均法、几何平均法以及特征值法三种计算方式方法确定权重,并求其平均值。
确定理想解并计算各评价对象到理想解的距离
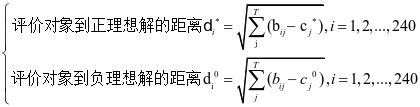 ,
,
计算评价得分的函数表达式如下所示:
 。
。
根据求解得到的综合评价得分排名,我们选取排名前50的供应商,由于数据较多,仅展示前20名供应商,如下所示:
表1供应商综合评价得分排名前50表
供应商ID | 得分 | 排名 | 供应商ID | 得分 | 排名 |
S031 | 0.9956 | 1 | S114 | 0.9779 | 11 |
S040 | 0.9944 | 2 | S150 | 0.9749 | 12 |
S055 | 0.9917 | 3 | S194 | 0.9746 | 13 |
S007 | 0.9901 | 4 | S086 | 0.9722 | 14 |
S080 | 0.9870 | 5 | S140 | 0.9712 | 15 |
S108 | 0.9865 | 6 | S139 | 0.9707 | 16 |
S131 | 0.9831 | 7 | S229 | 0.9703 | 17 |
S143 | 0.9813 | 8 | S218 | 0.9684 | 18 |
S151 | 0.9809 | 9 | S247 | 0.9673 | 19 |
S123 | 0.9797 | 10 | S098 | 0.9664 | 20 |
将无量纲化方法作为模型的环境参数,用分别用极小化,极大化法,极差化法,均值化法[5]四种不同量纲一致化方法对原始数据进行处理,然后按照TOPSIS模型进行评价,得到供应商排名图。
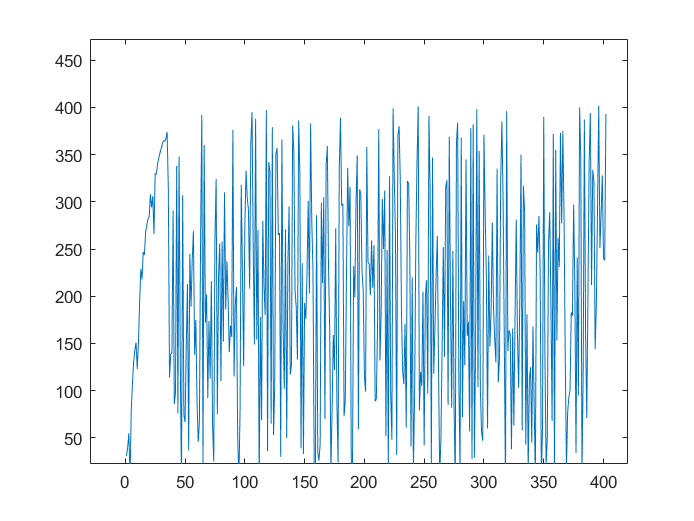
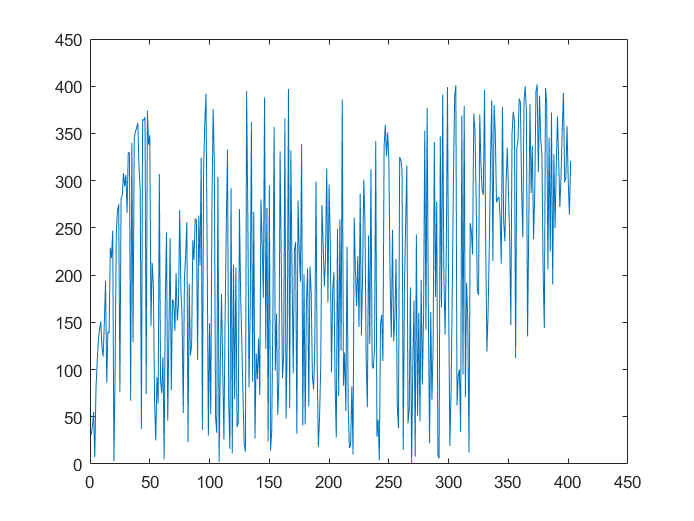
图1极小化处理后供应商排名图图2极大化处理后供应商排名图
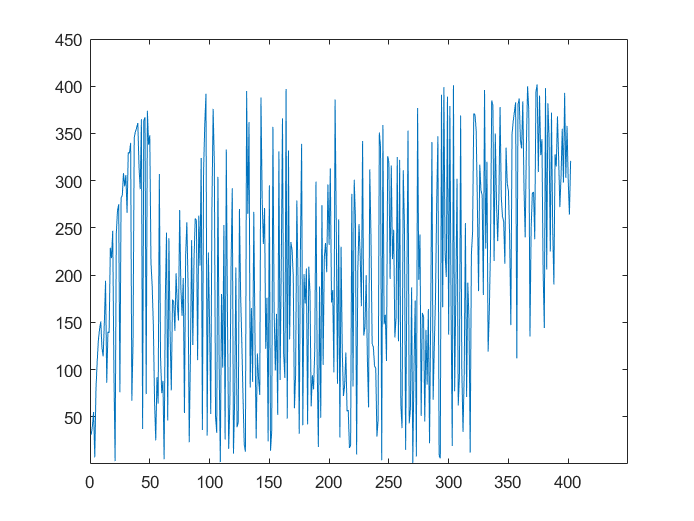

图3极差化处理后供商排名图图4 均值化处理后供应商排名图
结果分析:观察图1至图4可知,无量纲化处理的方式对排名有着较大的影响,从图2中可以看出极小化法的排名结果与其它的无量纲化处理方式有较大的不同,但是其它三种无量纲化的方法得出的排名结果相对于极小化法差距较小,具有一定的稳健性。
[1]李道有.瑞夏公司基于准时制的供应商选择优化研究[D].上海外国语大学,2021.
[2]马境蔓,李月强.造纸企业供应商的选择评价指标体系的构建[J].轻工科技,2021,37(03):147-149.