福建省晋江市磁灶中学 福建省 晋江市 362200
【摘要】:不等式恒成立求参数的取值范围问题是每年高考数学中的热点问题,这类问题几乎都是试卷中的压轴题,很多考生在处理此类问题时都显得有些力不从心, 基于此本文以高考数学试题为例,结合本人的教学经验在这里给同学们介绍四种如何解这类问题的方法与技巧。
【关键词】:高考数学 恒成立 方法与技巧
新课标下的高考越来越注重对学生的综合素质的考察,恒成立问题便是一个考察学生综合素质的很好途径,它常以函数、方程、不等式和数列等知识点为载体,渗透着换元、化归、分类讨论、数形结合、函数与方程等思想方法,在培养思维的灵活性、创造性等方面起到了积极的作用.近几年的数学高考中频频出现恒成立问题,其形式逐渐多样化,但都与函数、导数知识密不可分。
解决高考数学中的恒成立问题常用以下几种方法:①函数性质法;②分离参数法;③数形结合法;④消元转化法。下面我就以近几年高考试题为例加以剖析。
1、 函数性质法
在解决不等式恒成立问题时,一种最重要的思想方法就是构造适当的函数,然后利用相关函数的图象和性质解决问题,同时注意在一个含多个变量的数学问题中,需要确定合适的变量和参数,从而揭示函数关系,使问题更加面目更加清晰明了,一般来说,已知存在范围的量视为变量,而待求范围的量视为参数。例如;
例1.已知函数![]() ,其中
,其中![]() 为实数。
为实数。
(Ⅱ)已知不等式![]() 对任意
对任意![]() 都成立,求实数
都成立,求实数![]() 的取值范围。
的取值范围。
【分析】已知参数![]() 的范围,要求自变量
的范围,要求自变量![]() 的范围,转换主参元
的范围,转换主参元![]() 和
和![]() 的位置,构造以
的位置,构造以![]() 为自变量
为自变量![]() 作为参数的一次函数
作为参数的一次函数![]() ,转换成
,转换成![]()
![]() ,
,![]() 恒成立再求解.
恒成立再求解.
【解析】由题设![]() 知“
知“![]() 对
对![]()
![]() 都成立,即
都成立,即![]() 对
对![]()
![]() 都成立.设
都成立.设![]() (
(![]() ),则
),则![]() 是一个以
是一个以![]() 为自变量的一次函数.
为自变量的一次函数.![]() 恒成立,则对
恒成立,则对![]()
![]() ,
,![]() 为
为![]() 上的单调递增函数. ∴对
上的单调递增函数. ∴对![]()
![]() ,
,![]() 恒成立的充分必要条件是
恒成立的充分必要条件是![]() ,
,![]() ,
,![]()
![]() ,于是
,于是![]() 的取值范围是
的取值范围是![]() .
.
【点评】此类问题常因思维定势,学生易把它看成关于![]() 的不等式讨论,从而因计算繁琐出错或者中途夭折;若转换一下思路,可考虑变换思维角度“反客为主”,即把习惯上的主元变与参数变量的“地位”交换一下,变个视角重新审查恒成立问题,往往可避免不必要的分类讨论或使问题降次、简化,起到出奇制胜的效果。
的不等式讨论,从而因计算繁琐出错或者中途夭折;若转换一下思路,可考虑变换思维角度“反客为主”,即把习惯上的主元变与参数变量的“地位”交换一下,变个视角重新审查恒成立问题,往往可避免不必要的分类讨论或使问题降次、简化,起到出奇制胜的效果。
2、分离参数法
若所给的不等式能通过恒等变形使参数与主元分离于不等式两端,从而问![]() 题转化为求主元函数的最值,进而求出参数范围.利用分离参数法来确定不等式
题转化为求主元函数的最值,进而求出参数范围.利用分离参数法来确定不等式![]() (
(![]() ,
,![]() 为实参数)恒成立中参数
为实参数)恒成立中参数![]() 的取值范围的基本步骤:
的取值范围的基本步骤:
(1)将参数与变量分离,即化为![]() (或
(或![]() )恒成立的形式;
)恒成立的形式;
(2)求![]() 在
在![]() 上的最大(或最小)值;
上的最大(或最小)值;
(3)解不等式![]() (或
(或![]() ) ,得
) ,得![]() 的取值范围.
的取值范围.
适用题型:(1)参数与变量能分离;(2)函数的最值易求出.
例2.已知函数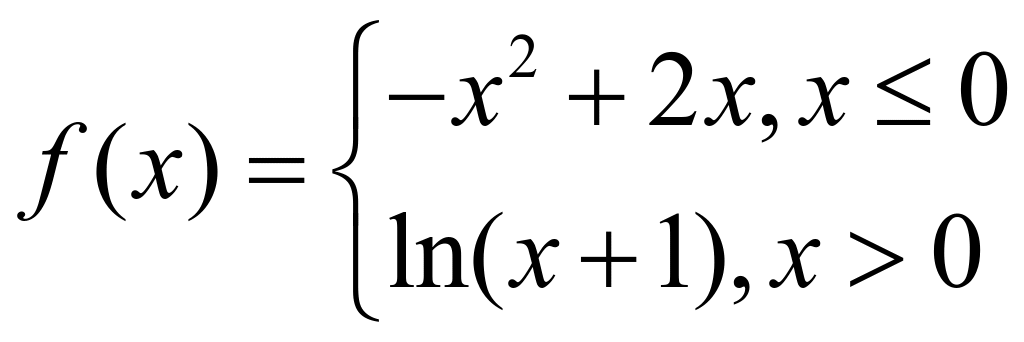 ,若|
,若|![]() |≥
|≥![]() ,则
,则![]() 的取值范围是
的取值范围是
![]() .
.![]()
![]() .
.![]()
![]() .[-2,1]
.[-2,1] ![]() .[-2,0]
.[-2,0]
【解析】∵ ∴由|
∴由|![]() |≥
|≥![]() 得,
得,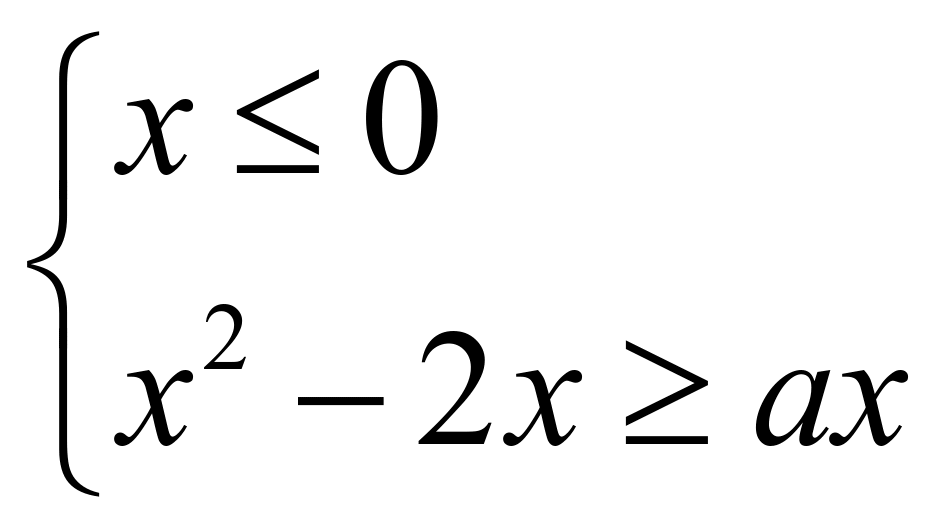 且
且![]() ,由
,由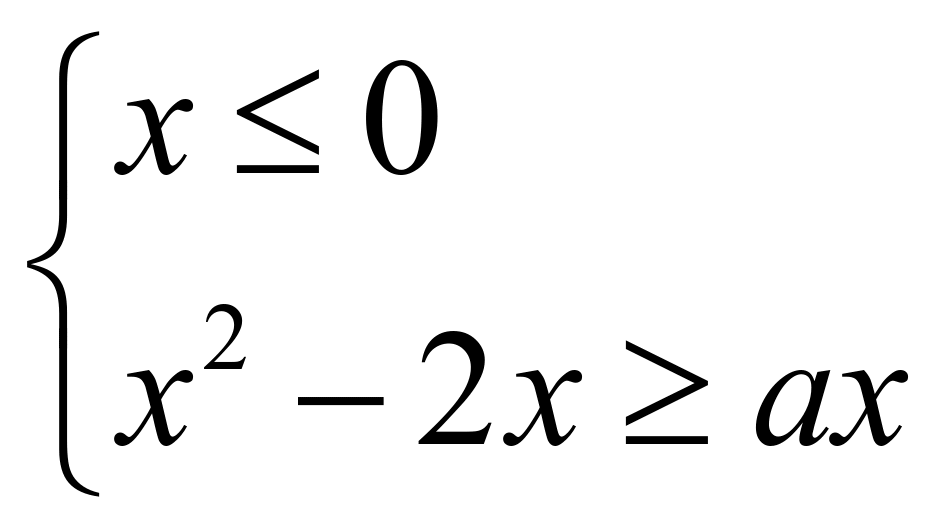 可得
可得![]() ,则
,则![]() ≥-2,排除A,B,当
≥-2,排除A,B,当![]() =1时,易证
=1时,易证![]() 对
对![]() 恒成立,故
恒成立,故![]() =1不适合,排除C,故选D.
=1不适合,排除C,故选D.
【点评】本题主要考查函数不等式恒成立求参数范围问题的解法,是难题。
例3.设函数![]() ,对任意
,对任意![]() ,
,![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是 .
的取值范围是 .
【解析】依据题意得![]() 在
在![]() 上恒定成立,即
上恒定成立,即![]() 在
在![]() 上恒成立.当
上恒成立.当![]() 时函数
时函数![]() 取得最小值
取得最小值![]() ,∴
,∴![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() .
.
3 、数形结合法
若所给不等式进行合理的变形化为![]() (或
(或![]() )后,能非常容易地画出不等号两边函数的图像,则可以通过画图直接判断得出结果,尤其对于选择题、填空题这种方法更显方便、快捷。
)后,能非常容易地画出不等号两边函数的图像,则可以通过画图直接判断得出结果,尤其对于选择题、填空题这种方法更显方便、快捷。
例4.已知函数![]() 若不等式
若不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是 。
的取值范围是 。
【解析】在同一个平面直角坐标系中分别作出函数![]() 及
及![]() 的图象,由于不等式
的图象,由于不等式![]() 恒成立,所以函数
恒成立,所以函数![]() 的图象应总在函数
的图象应总在函数![]() 的图象下方,因此,当
的图象下方,因此,当![]() 时,
时,![]() 所以
所以![]() 故
故![]() 的取值范围是
的取值范围是![]()

【点评】解决不等式问题经常要结合函数的图象,根据不等式中量的特点,选择适当的两个函数,利用函数图像的上、下位置关系来确定参数的范围.利用数形结合解决不等式问题关键是构造函数,准确做出函数的图象。
4、消元转化法
例5.已知函数![]() ,
,![]() 对任意的
对任意的![]() ,恒有
,恒有![]()
(Ⅰ)证明:当![]() 时,
时,![]()
(Ⅱ)若对满足题设条件的任意![]() ,
,![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的最小值。
的最小值。
【解析】(Ⅰ)略。(Ⅱ)由![]() 即
即![]() 恒成立,得
恒成立,得![]()
从而![]() ,等号当且仅当
,等号当且仅当![]() ,即
,即![]() 时成立
时成立
(1)当![]() 时,
时, ![]() ,令
,令![]() ,则
,则![]() ,则
,则![]()
因为函数![]() (
(![]() )的最大值不存在,但易知其上确界为
)的最大值不存在,但易知其上确界为![]()
![]()
(2)当![]()
![]() 时,
时,![]() 或0,
或0,![]() ,从而
,从而![]() 恒成立
恒成立
综合(1)(2)得![]() 的最小值为
的最小值为![]()
【点评】对于含有两个以上变量的不等式恒成立问题,可以根据题意依次进行消元转化,从而转化为只含有两变量的不等式问题,使问题得到解决.
从以上高考题的解法可知:以函数的观点作指导,用导数知识作工具,从研究函数的单调性、最值(极值)等问题入手,将恒成立问题转化为研究函数的性质问题,是确定恒不等式中参数取值范围问题的重要思考方法。对这类问题的处理,需要考生具备过硬的导数、不等式知识,并能灵活运用本文介绍的几种方法与技巧。在高三复习课教学中,有意识地给学生这方面的训练,对培养他们的数学综合素质是大有好处的。