促进课堂交流有效，问题串的设计方法

促进课堂交流有效，问题串的设计方法

陈滨

广东省湛江市第六中学 广东省 湛江市 524000

摘要：问题的有机串联，有效地克服了课堂教学中有些提问的细碎和离散，不仅能更简洁有效地驱动教学过程，还能让学生在解决系列问题的过程中学习提炼知识并获得解决问题的技巧策略．对问题串的设计进行更全面深人的研究和提炼方法，让它成为提升数学课堂师生交流有效的杠杆。

关键词：问题串 课堂交流 有效性

很多人认为问题串，就是若干个问题的简单组合，常常因缺乏目标指引和有机联系而使问题串沦落为一种廉价的问题堆积，有些案例虽然不乏精彩之处，却没有相应的设计章法，往往只是灵感所至，妙手偶得．问题串在相关文章和教学设计中已被广泛使用，它是问题导学理念下的一种有效的设计方式。所谓问题串，是指将若干个单个问题按一定顺序串联成的一个问题系列，该问题系列围绕同一主题且有明确的目标指向，其中的每个问题又围绕该目标并承担各自的功能．问题串中的问题不仅思维链条中的路标和思维方向的指引者，还可能促进课堂交流有效，它可以是数学问题本身，也可以是导向性、策略性或元认知性问题。

从问题走向问题串，其意义是为了实现系统论里所说的“整体大于部分之和”的功能而关键在于问题之间的有机联系，设计时要考虑设计什么问题、为什么要选择这些问题、按什么顺序排列等，而这些是有章可循的，如学生的认知规律，知识间的内在联系，目标与立意的层次等.

1. 按认知规律设置教学步骤，根据关步骤设计问题串

为保证数学的科学性和有效性，数学设计除了要求把内容实质，了解学生实际外，还应符合认识规律．数学数育心理学依据学生认知规律对诸如概念的形成、概念的同化、公式定理的掌握、思想方的形成等都提出了教学建议，并给出了一些不可缺少的关键步骤。数学新知识都不是无中生有的，它是一种推陈出新。假如我们将核心知识的获得作为一个“终点”的话，必可以在学生那里找到与之直接相关的原有的知识或经验，即是学生的最近发展区，可以把它作为数学的“起点”。在这个前提下，设计的任务便主要是在起点和终点之间给出一系列的关键步，形成过度性中间点（简称“中点”），然后根据各“中点”所承担的功能，提出有一定空间的问题系列。如此，设计步骤归结为：①确定好终点；②寻找到起点；③分析出中点，并设计相应问题。

案例1《图形的旋转》，该内容在人教版数上仅有几幅图片加上寥寥几行文字，那么学生如何获得图形旋转的概念呢？

起点：通过逻辑判断和经验分析，找出学生已有的与核心概念相关的经验或知识，作为数学的起点。图形的平移和轴对称，下位与并列的概念都有，“向一个方向移动一定距离”的说法及其意理解是学生已有的经验，可以作为数学的起点。

终点：图形旋转的概念，“绕着平面内某一个点O转动一个角度”。

问题1　先从剪纸引入，明确主题：旋转,可以适当介绍我国剪纸是人类非物质文化遗产.然后在屏幕上显示“剪纸艺术欣赏”，学生在观察欣赏情景中自然引入“旋转”.引入课题《23.1旋转》.这每组剪纸的两个图形之间，其中一个是经过哪种图形变换而得到另一个图形的？

教师追问1：情况2是轴对称，当时我们在学习时主要研究了它的哪些方面？

教师追问2：轴对称的概念和性质是什么？

问题2 先让学生举出一些生活中的实例，再观察实例：旋转的风车，转动一定角度的钟表，有天津特色的解放桥闭合和打开的状态.思考：如何描述这种图形的变换？

问题3发给学生中间有挖掉一个三角形洞的硬纸板，让他们依据老师的描述画出将这个三角形旋转后的三角形.在一张白纸上任取一点O和点P．如果让它绕一个定点O旋转90°，得到几个结果？

教师追问1：如果让它分别绕点O和点P顺时针转动90°，得到几个三角形？

教师追问2：如果让它绕定点O顺时针旋转，得到几个三角形？

教师追问3：给定怎样的条件才能使旋转后的图形唯一确定？

需要指出的是，关于中点的设计，问题越多，意味着铺垫越多，越容易导出结论，达到终点，这是其优点；但这样每个问题的思维空间和跨度就越小，真正意义上的探究也就越少，这是其不足设计的艺术在于如何找到“导出结论的难易”与过程中“思维含量的多少”两方面的平衡点，让我们课堂数学交流更有效.

2.按阶段任务设置数学环节，根据目标指向设计问题串

有些数学知识的学习不能归于某种单一类型，有时可以按需要把多种方法有机地结合起来。一种很自然的设计方法是，先按完成认知任务的实际需要确定与之相应的教学环节，再根据各环节的目标来设计指向性的问题系列。一般这样的设计步骤归结为：①任务分解：将总的认知目标按需要分解成阶段性认知任务；②环节确定：按阶段性认知任务来设置若干个对相应的教学环节：③问题设计：根据各环节的目标指向来设计直接的问题。

案例2《正比例函数》的设计

问题1：我们小学已经尝过正比例的要念，你能举出一些两个量成正比例的例子吗？

问题2：所举的例子中有几个变量？不变的是什么？

问题3：如何用函数的观点去解释上述问题？

问题4：请同学们阅读课本，并举例说明你对正比例函数概念的理解.

问题5：用定义判断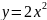 和 是否是正比例函数，为什么？

该设计初看有点直来直去，没有什么新意．但细细品味，发现却是环环相扣，环环紧扣关键处；步步为营，步步击中要害点、总任务分解成五个阶段任务：激活原有相关概念，揭示的新视角，引发新的理解，阅读理解并举正例支撑，反例析，五种认知任务对应着五个环节，五个目标对应着五个指向明确的问题，这样设计出的问题串既补实无华，又简洁自然，让教师与学生，学生与教材进行有效数学交流.

3.按教材内容提取教学要点,并根据要点寓意设计问题串

道理不能用直白的方式告知学生，最好的方法是提供恰当例子或问题，让学生在解决问题的过程中自主地感悟出来．数学学习中的很多地方都要遵循这一原则．如果把这些“道理”称为“要点”的话，有时说明一个大道理需要若干个“要点”的支撑或整合，从而也就需要把这些蕴含“要点”的单个问题中联起来，形成问题串．这种问题中的设计步骤可以归结为：①理解教材，即把教材内容弄懂吃透，领悟其实质；②提取要点，即根据数材内容概括出“段落大意”；③根据要点离意选择或设计问题。

案例2《用二次函数解决利润代数问题》的设计

问题1：某商店有一种钢笔，每支成本价是2元，售价是5元，卖这种钢笔每支可以赚多少钱？

问题2：某商店有一种钢笔，每支成本价是2元，售价是5元，现在将售价降低1元，卖这种钢笔每支可以赚多少钱？

问题3：某商店有一种钢笔，每支成本价是2元，售价是5元，现在将售价提高1元，卖这种钢笔每支可以赚多少钱？

问题4：某商店每天售出5支钢笔，每支可赚2元，每天卖这种钢笔可以赚多少钱？

问题5：水果店有一箱苹果，共50个，准备盒装的形式卖给顾客.5个装一盒，这箱苹果能装多少盒？

问题6：水果店有一箱苹果，共50个，准备盒装的形式卖给顾客.5个装一盒，卖出一盒赚12元，这箱苹果如果卖完共赚多少钱？

问题7：某商店有一种钢笔，每支成本价是10元，标价是15元，现在打8折优惠卖出，每天售出20支，每天卖这种钢笔一共赚多少钱？

问题8： 某商店钢笔成本价是10元，现将价格提高50%后作为标价，然后打8折优惠卖出，一共赚了40元，这种钢笔卖了多少支？

问题9：某商店将进价为8元的商品按每件10元售出，每天可售出200件，现在采取降低商品售价增加销售量的办法增加利润，如果这种商品每件的销售价每降低0.5元其销售量就增加15件，问应每件降价多少元时，才能使每天利润为640元？

问题10：某商店将进价为8元的商品按每件10元售出，每天可售出200件，现在采取降低商品售价增加销售量的办法增加利润，如果这种商品每件的销售价每降低0.5元其销售量就增加15件，问应每件降价多少元时，才能使每天利润最大？

这里每个问题的解决，不能停留在问题答案本身，而应着力于问题背后的“要点”的感悟或提炼，假如单个的问题解决是隐性“要点”显性化的，过程，而问题的整体把握则是零散“要点”系列化从而实现整体口标的过程，本案例中，如果学生能自主感悟出各要点并能把它们中联起来，对利用二次函数解决利润代数问题非常简单并深刻。

这种设计方法的关键是确定准确的“要点”，设计恰当的问题．对于如何揭示“要点”，教师本身的数学素养就显得尤为重要，假如照搬照套，机械理解，往往交流有效性较低．而恰当的问题是指既能直接提炼出要点、又简洁有趣的问题，这使我想到了生活背景，让学习更有效的应用于生活。

上述三种问题串的设计方法是根据分步来串联设计的，还有一类方法则是根据分类来并列设计．如数学上的很多问题其实质是寻找不同对象的共同之处，在变化中发现变化规律或不变之处等，问题串的每个问题，承担的角色是既能反映变化又能体现共性的正例支撑，所以只需要考虑覆盖性和典型性的前提下按一定顺序并列.

例如，《分式的性质》设计就是用类比的方法

问题1：小学我们学习了分数的性质，分数有什么性质呢？

问题2：我们怎样用字母来表示呢？

问题3：根据分数性质，请同学们总结出分式的性质？

这种并列式问题串我们经常用到，并且与学生交流起来效率最明显.

问题串的设计是为了让数学教学更贴近数学本质，让数学学习更符合认知规律，从而让数学课堂交流更有生机和更具效益.

参考文献：

王先进 谈问题串的设计方法. 数学通报，2012（7）