把握本质 探索规律-----《乘法分配律》的探索之路

把握本质 探索规律 ----- 《乘法分配律》的探索之路

翟新赟

烟台市芝罘区青年路小学 山东省烟台市 264000

摘要：计算教学是小学数学的基础，它贯穿于小学数学的始终。而简便运算则是计算教学中训练学生思维的重要手段，它是学生通过运用所学的运算定律和数字的基本规律，将一些复杂的算式，迅速地计算出来，从而有效地提升计算的效率。但是，教学中，我们不难发现简便运算恰恰是学生学习的易错点和难点。在四年级简便运算单元的学习过程中，交换律和结合律的运用，学生能够灵活掌握，并能做到触类旁通，可是学习了乘法分配律后，却非常容易混淆，出现运算律乱用现象。如用简便方法计算25×（8×4）时，经常有学生误用乘法分配律，将上式算成25×8+25×4。怎样才能让学生真正的掌握运算规律呢？下面结合自己《乘法分配律》的教学实践，阐述一下自己的经验和做法。

关键词：小学数学；教学实践；加强练习
   一、由表及里，解释规律。

在教学《乘法分配律》时，教师常常将侧重点放在观察算式的外在形式上，淡化了内在算理的阐释，导致学生只会机械地记忆规律，不能理解规律的内涵本质。笔者认为在教学中，我们既要重视算式的外形结构，更要重视内涵的理解。

1. 借 助乘法意义，解释算理。
   《乘法分配律》一课教学时，创设芍药和牡丹花的排列图的情境：芍药有6列，一列有3棵。牡丹有这样的4列，每一列也有3棵。芍药和牡丹一共有多少棵？

把芍药和牡丹的列数各增加一列，每列的棵树也增加一棵。一共有多少棵？

继续增加行数和列数，一共有多少棵？

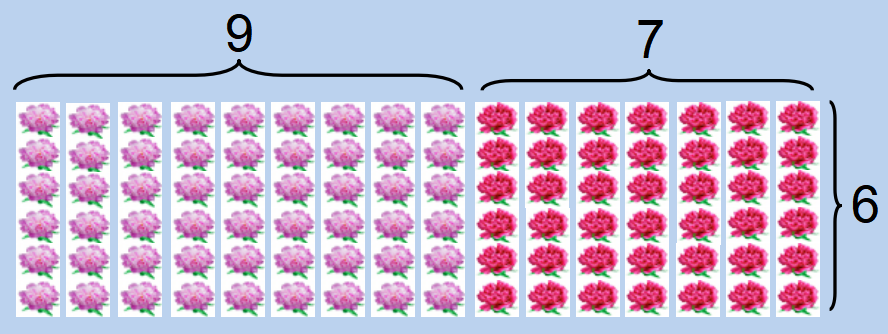
通过一个情境，创设三道题目，引导学生用两种方法求出一共有多少棵花，学生利用已有经验，轻松的解决3个问题，得到3组等式。结合情境图，启发学生从乘法的意义的角度分析两种算式之间的相等关系。如：6×3+4×3=(6+4)×3。根据乘法运算的意义：即6个3加4个3等于（6+4）个3。然后，学生通过想象不断地扩大行和列的数目，写出无数组等式模型，这些等式都可以用乘法的意义解释，进一步引导学生从形式及意义上初步感知乘法分配律的模型。这样通俗易懂，便于学生理解和记忆，也有利于学生灵活运用。

2.借助几何直观，建立模型。
在学生得出规律之后，由芍药和牡丹花演变到长方形，借助几何直观，让学生经历数与形的对应过程，加深理解。如下图：

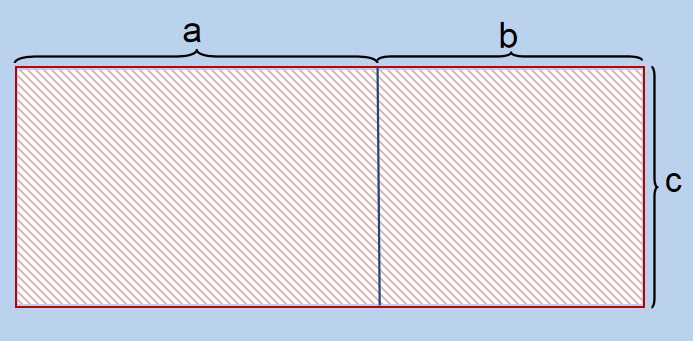
大长方形的面积可直接用长×宽，也可以分别求出两个小长方形的面积再相加，因此也可以得出（25+35）×8=25×8+35×8。利用信息技术功能拖动中间的竖线，通过不断变换两部分的面积，让学生感受到总面积不变，进一步理解乘法分配律的几何意义，再次证明乘法分配律的合理性。由图形到面积，将抽象的知识具体化，为学生在头脑中建立一个乘法分配律的几何模型，将乘法分配律的模型深深地印在学生的脑海里。

3.结合旧识，加深理解。

学生发现并归纳出乘法分配律之后，教师要引导学生联系旧识，打通新旧知识之间的关联，帮助学生形成知识网络。通过回顾“12×3”竖式计算的过程和计算长方形周长的方法，从而让学生明白原来过去的知识中也曾有过乘法分配律的影子。使学生在学习新的知识时能够与以往的知识进行很好的衔接，加深学生对新知识的理解。

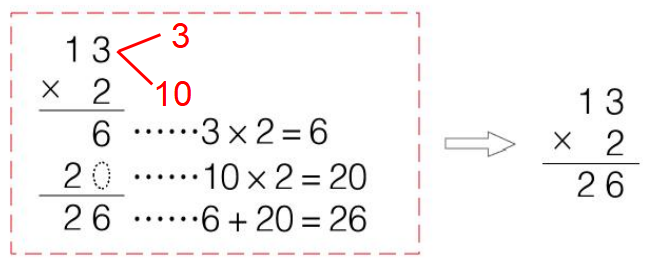
二、把握本质，加强对比练习。

学生对乘法结合律和乘法分配律混淆，主要原因是没有把握这两条规律的本质，不清楚各自的应用背景。为了促进学生对规律的内化与掌握，在练习的设计上要引导学生理清以下两点。
1.把握规律的本质。
乘法结合律实际上是在保证每个因数只乘一次的前提下，改变乘的顺序，积不会改变，其着力点是“乘的顺序改变”，只涉及一级运算。乘法分配律的着力点是“算式结构的改变”，即将（a+b）×c转化成a×c+b×c，或者将a×c+b×c转化成（a+b）×c，它涉及两级运算。因此，要引导学生讨论“乘法结合律和乘法分配律有什么区别”，进而掌握两者的本质。
2.加强对比。
练习课可以设计一些形似而质异的对比练。
(40+4)×25   (40×4)×25

65×16+35×16   65×16×35×16

(125+25)×8×4   (125×25)×8×4
通过对比，让学生区分乘法结合律和乘法分配律的结构特征，乘法结合律适应于连乘的结构，乘法分配律适用于乘加乘减结构含有两级运算的算式。通过对题目的交流与辨析，使学生进一步明晰两条规律运用的背景。
  再如简算404×25，引导学生思考：如果用乘法结合律进行简算，该如何拆数？让学生明白：因为在连乘结构的算式里才能运用乘法结合律，所以把404拆成101×4。接着让学生思考：如果运用乘法分配律进行简算，又该如何拆数呢？通过交流讨论达成共识：因为在“乘加”或“乘减”结构的算式里才能运用乘法分配律，所以把404拆成（400+4）。

    三、边念边写，巩固应用。
简算55×101时，学生在变形中常见的错误有两种：一是变形成55×100+1，二是变形成55×101-1。面对这样的错误，教师可以让学生从题目上入手，引导学生这样念。先念：101个55，分解成100个55，再加1个55。这样学生就不会发生变形错误。即：55×101=100×55+1×55=5500+55=5555，之所以省去55×101=55×（100+1）的过程，主要是想提醒学生从乘法意义的角度去思考，减少错用乘法结合律的可能。
用乘法运算律简算的题都可以让学生念念有词，边念边写。例如：61×139-39×61=61×(139-39)=61×100-6100先观察算式特点念：两乘一减，含有相同因数。再念变形过程：139个61减去39个61，相同因数提出来，不同因数先相减。熟练了也可以简单说成“提”因数，“减”打包。

念念有词，边念边写，一方面以简短口令指挥行动，让学生计算更专注，另方面学生念的是算式的特点、变形的过程，让学生在简算时更关注寻找特点、思考算理、运用算法，混用的现象自然会降低，正确率自然会提高。

总之，针对学生在运用乘法分配律开展简便计算时所出现的诸多错误，教师应从规律的本质入手，加强研究分析，并积极探寻对策，把握本质，精心设计练习，使简便运算与规律的本质紧密联系起来，帮助学生理解数学的内涵、领悟计算的魅力，感受数学的规律美。

参考文献：

1. 雒红芳.核心素养的小学数学教学生活化分析[J].考试周刊,2020(A5):71-72.

2. 谢宝兰.小学数学教学模式创新探究[J].知识窗(教师版),2020(12):14.

作者简介：姓名：翟新赟，出生年月：1987.10，性别：女，学历：本科，民族：汉族，籍贯：山东淄博，单位：芝罘区青年路小学，现在职称：二级教师，研究方向：小学数学。

3