物理学的时间问题

物理学的时间问题

倪明

江苏省农业科学研究院 江苏省 南京市 210001

摘要：在一定速度中‘一段行程’就是这段行程的时间的表征，那么‘运动的体长’也是‘运动态的时间表征’。电子两端经过计时器有‘开始和结束’两个时刻，另一方面 地面实验室及计时器对电子运动，同是那个开始和结束，但是发生‘时间缩短’，叫时间慢！（解释洛伦兹实验。）由于惯性系的‘运动态时间’是互相在对方的‘静止态时间’里表现的，这样造成同一事物和现象在两个惯性系里的‘时间间隔或时间排序不一致’。

关键词：传统时间和相对论时间；静止态和运动态；变化累积量

‘时间，空间，质量，能量，运动和静止’是普通物理学的基本概念，由它们表述的规律是物理学基础理论内容。‘狭义相对论’在历来实验事实的基础上，以新的‘静止-运动’观为基本点，革新了基础理论——牛顿力学的发展。其中带来新的‘时空观’，也带来 我们学习者对 相对论时间和传统时间 及它们的关系 如何理解的问题？

一、时间常识梳理

1）传统时间观念的形成：客观世界或一个事物 都有整体的‘象’（存在），人类的思维 在一定程度上 经整合反映这些‘象’：基本情况是 万物在空间里，另一种基本情况是“万物变迁不已”。而‘变迁’一方面是‘某些特征在变’，一方面保持这种变的形式，如此造成万物的时间——既‘流逝又持续’。如‘青年’是指从18岁到30岁，‘一支烟的功夫’指一支烟抽完的时间；哪怕是‘稍纵即逝’的微观粒子也有‘从生到灭’的形式，钟针在钟面上‘均匀旋转’没有改变，它的‘均匀旋转时间’就继续下去，客观世界包含一切事物，因此它的‘流逝和持续’是永恒的。

2）时间的‘先后’不可逆性。有‘时间’就有‘时刻’，‘一维的时间’内涵 就是排除‘空间的要素’只表达‘先后时刻’的次序，是不可逆的——否则就失去时间最本质的特征。于是在‘时间的象’中，就有各种事情或现象 发生的次第，人类因此作抽象数学的排序（如牛顿自述是“数学的时间”），例如我们说‘张三比李四 大五岁’，只表达出生的排序，间隔5年；对于‘客观世界’它是无始无终的。难怪传统时间有‘流逝性’而无速率。

3）时间的量度 是从‘某时刻到下一时刻’的‘变化的累积量’的等时比较，例如‘运动速度’是‘行程累积量’与计时器内‘某种变化累积量’的‘等时’比较；‘汽车比飞机慢’指‘在等时间’内 汽车的行程较少。‘时间延长’和‘慢’的区别：‘时间延长’表达 在完成‘相等变化累积量’下 其时间比较长。因此对‘同时刻’的认识是‘关键’。

决定‘时间长短’的因素有两条：可变化量的限定 和变化的快慢。

4）地球地理的局部时间‘象差’。假如在‘北温带’的某地 在夏季的某一天，白天是 太阳从5点开始升起，到下午19点落下，而在南半球‘南温带’正在冬季，在此当天 南半球某地的白天是 太阳从7点升起，到下午17点落下；这里 用来计时的钟的构造和钟针的转速 完全一致，计时差别却如此大！但是我们坚信两地有‘共同时刻’，处于‘共同时间’，因为钟是按照每一秒等于 1/86400‘平均太阳日’设计的，在这里‘钟时’代表‘共同时间’，理由就是来自我们学习过的‘中学地理’关于‘地球和太阳系’的知识，如果我们不相信这种‘共同时间’，也就是不接受‘太阳系的学说’。 结论是：局部时间就是 地球上局部地区 的时间的‘象’，共同时间指‘地球对太阳运动’的大局的‘时间的象’（存在）。

二、‘狭义相对论’的大致论点

1）放弃‘以太绝对静止说’而认为：‘静止和运动’是空间中物体的关系，静止就是物体互为静止，运动就是互相‘以对方’是运动（互为又叫相对），互相在对方的时空中。组成互相运动关系的 就叫‘运动参照系’，其中‘匀速直线运动’参照系简称‘惯性系’，于是惯性系就同时具有‘惯性静止态和惯性运动态’的两方面姿态——静止或运动是对对方表现的。（例如月亮只绕地球转，地球也绕月亮转 在月亮的轨道上。地球‘自转’是对 除了地球的宇宙全部星体，宇宙全体也围绕地球转，都是‘非惯性系’的互相关系。又例如‘匀速运动的汽车或飞机’和地面的关系 近似做为惯性系。）

‘狭论’有惯性系运动的三个数学公式 来比较惯性系的‘近光速运动态’和它的‘静止态’的物理表征。

静止态的物理表征如‘物体的线长度、变化的快慢程度，质量的大小’都同于牛顿力学里的，这里的静止态物理表征也包括一切‘远光速运动’事物的表征，是近似包括！

但如果惯性系的相对运动是‘近光速的’，那么运动态的三项物理表征则遵守‘近光速运动效应’的规律表现出来。表达‘相对论运动效应’规律的数学关系公式是：‘运动态事物的变化快慢’/‘其静止态变化快慢’＝‘事物运动态的沿运动方向的体长’/‘其静止态沿运动方向的体长’＝静态质量/其动态质量 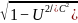＝ （惯性系运动速度U＜光速C），运动公式还表明，相对运动速度有极限，不能超过光速

（这是和牛顿力学的区别）！

注意：‘变化快慢的公式’和‘体长公式’是同步一致的关系，和质量公式成反比关系。

2）‘狭论’立论的第一个‘前提’：“对各个惯性系 光在真空的所有方向都等于30万公里/秒。” 在取消以太中任何一点都是绝对静止点的想法以后，那么光速恒等于30万公里/秒就依据的是 在宇宙里任何惯性系包括其静止态时间 都是平等的，且事实如此（人类测量光速和科学推断来自遥远‘作变速运动’的星球的光速 就是在地面的静止态下）。

3）运动效应的根据，来源于洛伦兹近光速电子实验，实验首次发现：电子沿运动方向的体长 发生收缩（变扁），同时电子质量变大的效应，当电子速度越接近光速，这种效应越显著，以致电子速度不能超过光速！反映这种效应的规律就是上述的数学公式。洛伦兹还由此推断：运动惯性系的‘时间也相应变慢’。（在科学家眼里，高级和低级的各种运动变化形式 一定都包含最基本的‘位移运动’形式；洛伦兹曾认为 运动效应是对以太的效应。）

4）导出‘能量和质量的当量’公式。‘运动态’就等于具有‘动能’态。‘质量变大的公式’反映‘速度改变与质量改变’的关系，那么在公式里一定也包含‘动能改变与动质量改变’的关系！E=M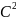 公式是狭义相对论从‘质量的运动公式’导出的最著名的成果！

三、相对论的时间 ——由于惯性系的运动态时间 是互相在对方的静止态时间里表现的，这就造成‘同一事物和现象’在两个惯性系的静止态的‘时间间隔或排序不一致’！

1）洛伦兹是怎样发现‘运动电子’变扁和时间变慢的？以下用相对论的观点来分析。 洛伦兹做电子运动的实验，电子对‘计时器’是‘运动态’的，测量原理：电子速度（v）ב经过电子直径的计时t’＝直径d。那么洛伦兹怎么判定电子直径变短的？本来 他测量慢速运动电子直径D＝速度Vב计时T’，当电子速度逐步增加到近光速时（通过控制电场来控制和计算电子速度），本来 时间和速度应该是反比关系，应该是t，但是 他发现时间没有成反比，而是‘t’，更短了，则表明直径D也缩短了。那怎么时间也慢了？

回答：在一定速度中‘一段行程’就是 这段行程的时间的表征（行程/速度=时间），那么‘运动的体长’也是‘运动态的时间表征’，因为‘体长上所有的质点’都以相同的速度 运动过 相当于这段体长的长度，这样 在速度中 这段体长就表征‘运动物的这段运动时间’。怎么不叫‘时间减短’？ 因为电子直径不是‘减短’，而是缩短，并且电子质量变大！

‘慢’的原意是‘同种变化量’的‘等时相比’，‘时间慢’怎么解释？

‘近光速运动电子’与‘地面及实验室’各是两个‘惯性系’，它们之间的物理表征不是在静止关系的。

在实验里，‘近光速运动电子’对实验室表征一段‘在实验室里的时间’是电子直径d，同时也由实验室的计时器显示时间是t；另一面是‘地面实验室及计时器’对电子反向运动，对‘电子系’表征的时间是电子直径D。（设实验室计时器上一点 经过电子两端，在‘电子系’里表征的时间是‘经过电子的时间’，由电子的体长D来表征（时间= D/相对速度），而‘D体长’在电子内部静止。）

这是否‘同时比较’？分析如下：电子两端经过计时器 有‘开始和结束’的时刻；另一面 计时器对电子反向运动经过电子两端，同是‘此开始和结束’，就是‘在同时’的电子体长和时间各不同，所以‘时间慢’的意思指‘同时’中 时间间隔较短的！

还有 计时器对电子反向运动 经过电子体长，计时器显示它的‘变化累积量’ 仍是此‘变化累积量’t，而此‘运动态的计时t’的时间间隔在‘电子系’里是长的行程D长度。结论：‘同样的变化量’t 在电子系的时间表征D 长于在‘实验室系的’时间表征d，表明 在运动态的计时器里‘表征时间’的变化 是慢的！

质疑：为何前者电子体长缩短成d 叫‘时间慢’，而后者运动行程是D也叫时间慢？分析结果：相对论的原理是 时间一定和运动的行程密切联系成正比关系——运动从一点到另一点 才产生时间间隔，‘运动的体长’缩短 则证明‘运动物的时间’变慢。计时器不表征‘体长’，计时器的运动行程等于对方参照系里的静止态电子体长D，恰恰二者的结果是一致的——运动态的计时器的时间变慢。

（D和d都同时表征相对运动的行程和时间，说明‘运动效应’维护惯性系的相对速度。）

2）‘狭论’科普书里的‘同时性的相对性’假想实验。实验描述：在‘列车惯性系’的车厢的中点，设有‘闪光灯’同时向车厢两端发射两个‘光脉冲’（沿列车运动直线）等距离地同时到达终点，因为这是在列车系的静止态中。（令人想起伽俐略描述的‘大航船’。）

另一方面 列车系相对地面具有‘近光速运动’，然而那两个光脉冲对地面还是以不变的光速运动，在它们各到达终点时，车厢两端的终点位置已经一齐向前移了位。这样 对于地面 向后运动的光脉冲是早于车厢的 到终点结束，向前运动的光脉冲迟于车厢的结束。这样它们在两系的时间排序已经完全不同了！（‘长度并时间’的运动效应 及光波的‘多普勒效应’都不影响此结果。）

3）兀介子实验 兀介子只能存在平均‘2·6×10的负8次方’秒就衰退掉。当兀介子以‘光速的0·98倍’在地面运动时，按照此时间计算，它只能运动7·64米的路程，但是实测它的行程等于38·2米，用‘38·2米/0·98倍光速’，得其存在时间却是‘ 1·3×10的负7次方’秒；而‘地面系’也反向以‘光速的0·998倍’对 兀子运动，那么地面收缩 而‘38·2米的地面长度’也缩短成7·64米，静态兀子的存在期还是‘2·6×10的负8次方’秒。

代入相对论的‘时间公式’（‘2·6×10的负8次方’秒/‘效应系数’）来计算，‘近光速运动的 兀子存在期’与相对论‘理论计算的存在期’基本符合。

总结以上例子：由于惯性系的运动态时间 是互相在对方的静止态时间里表现的，这就造成同一事物和现象在两个惯性系里‘时间间隔或排序不一致’；那么对于宇宙所有惯性系的‘一同存在’，统一的时间不存在。故用‘理论物理学’来讲 传统时间仅是在地球参照系的时间，体长联系时间也是的；造成此结果的原因就是，物理学界被迫取消‘以太说’，承认‘光速守恒’和‘运动效应’的发现。