广东省深圳市福田区红岭中学 广东深圳 518000
摘 要:当前新高考、新课程、新课标、新教材在全省各高中学校全面铺开实施,在“四新”背景下,本文以一节排列组合的习题课为例,设计出合适的题目来提升学生数据分析核心素养。
关键词:核心素养;数据分析;排列组合;思想方法
1概述
2020年秋季开始,高中全面进入新高考阶段。其中,2020级新生开始使用新课标、新教材。至此,新高考、新课程、新课标、新教材在全省各高中学校全面铺开实施。在“四新”背景下,高中数学教师如何迅速适应新的教育教学要求?如何有效提升高中生数学核心素养?针对这一系列问题,本人的名师工作室一直在努力摸索和探寻答案。
数学核心素养的本质就是指导学生通过数学的角度看待问题,条理清晰地进行理性的思维和严密的证明,通过逻辑推理,清晰准确表达结果。做事思路清晰,行事干练,这是受益终身的数学核心素养。高中阶段的数学核心素养有六个,由参考文献[2]可知,一般情况下,学生对六大核心素养掌握情况存在差异,其中数学建模和数据分析对于其他四个素养的依赖性较大,是更高维度的核心素养。
排列组合是高中数学非常重要的研究内容。由于其在高考分值上所占比重不高,导致了很多老师没有着重研究这部分的教学方法,纯粹依赖学生的“天赋”完成教学。但排列组合对学生数据分析的核心素养要求非常高,这也导致了很多学生“望题止步”。本文以一节排列组合的习题课为例,浅谈课堂教学中如何提高学生数据分析素养。
2教学片段
2.1天下谁人不识君
类比物理学中的并联与串联电路理解两个计数原理,分类加法计数原理可类比并联电路,分步乘法计数原理可类比串联电路,这样可以形象地理解两个计数原理。
例1 如图,一条电路从A处到B处接通时,可以有多少条不同的线路?
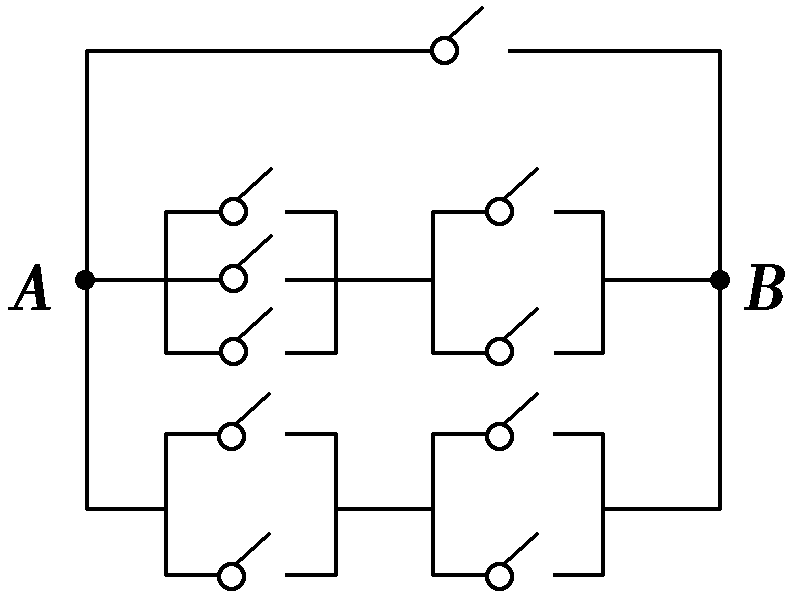
[解析] 第一类:有一条线路。第二类:有3×2条线路。第三类:有2×2条线路。根据分类加法计数原理,从A到B接通时共有1+3×2+2×2=11种不同线路。
[设计意图] 本题是在掌握两个计数原理公式的基础上,利用两个计数原理的公式进行类比并直接运算,考查学生的数学计算以及数据转化与化归能力。
2.2多才多艺,才高八斗
生活中总有各种“多面手”,这类问题需要使用特殊元素或者特殊位置优先考虑的思路。解答的重点是关注“多面手”,进行合理恰当的分类是解题的关键。
例2 在7名学生中,有3名会下象棋但不会下围棋,有2名会下围棋但不会下象棋,另2名既会下象棋又会下围棋,现在从7人中选2人同时参加象棋比赛和围棋比赛,共有多少种不同的选法?
[解析] 选参加象棋比赛的学生有两种方法:在只会下象棋的3人中选或在既会下象棋又会下围棋的2人中选;选参加围棋比赛的学生也有两种选法:在只会下围棋的2人中选或在既会下象棋又会下围棋的2人中选。互相搭配,可得四类不同的选法。
第一类:从3名只会下象棋的学生中选1名参加象棋比赛,同时从2名只会下围棋的学生中选1名参加围棋比赛有3×2=6种选法;
第二类:从3名只会下象棋的学生中选1名参加象棋比赛,同时从2名既会下象棋又会下围棋的学生中选1名参加围棋比赛有3×2=6种选法;
第三类:从2名只会下围棋的学生中选1名参加围棋比赛,同时从2名既会下象棋又会下围棋的学生中选1名参加象棋比赛有2×2=4种选法;
第四类:2名既会下象棋又会下围棋的学生分别参加象棋比赛和围棋比赛有2种选法.
∴共有6+6+4+2=18种选法。
∴共有18种不同的选法。
[命题意图] 数学运算是数学活动的基本形式,也是演绎推理的一种形式,是得到数学结果的重要手段。数据分析依赖于数学运算,分类讨论是数据分析中的一个重要思想。
2.3最是橙黄橘绿时
解决涂色(种植)问题的一般思路:①按区域的不同,以区域为主分步计数,用分步乘法计数原理分析;②以颜色为主分类讨论,适用于“区域、点、线段”等问题,用分类加法计数原理分析;③将空间问题平面化,转化成平面区域的涂色问题。
例3 将红、黄、绿、黑四种不同的颜色涂在如图所示的图中,要求相邻的两个区域的
颜色都不相同,则有多少种不同的涂色方法?

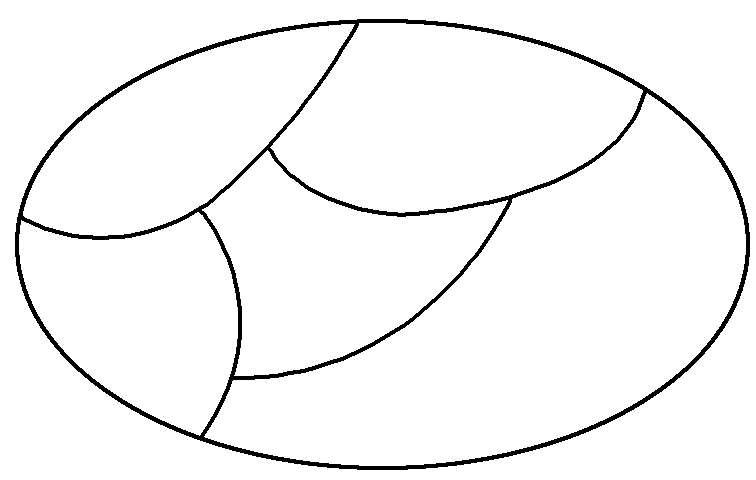
[解析] 给图中区域标上记号A,B,C,D,E,如图所示
①当B与D同色时,有4×3×2×1×2=48(种),
②当B与D不同色时,有4×3×2×1×1=24(种),
故共有48+24=72种不同的涂色方法。
[命题意图] 分析思路为确定A区域的涂色方法⇒确定B区域的涂色方法⇒确定C区域的涂色方法⇒确定D区域的涂色方法。涂色问题一般是综合利用两个计数原理求解,是学生需要掌握的分析数据的常用方法。
2.4柳暗花明,模型先行
模型法就是通过构造图形,如树形图、表格等,利用形象、直观的图形帮助我们分析、解决问题的方法。模型法是解决计数问题的重要方法。
例4 三人传球,由甲开始发球,并作为第1次传球,经过5次传球后,球仍回到甲手中,则不同的传球方式共有多少种?
[解析] 如图:甲→□→□→□→□→甲。第一个空与第四个空不能是甲,分三类讨论:
(1)若第二个空是甲,则第一个空有2种选择方式,第三个空有2种选择方式,第四个空仅有1种选择方式,所以有2×2=4种方式;
(2)若第三个空是甲,同上,有2×2=4种方式;
(3)若第二个、第三个空都不是甲,则仅有如下两种传球方式:
甲→乙→丙→乙→丙→甲;
甲→丙→乙→丙→乙→甲。
所以共有4+4+2=10种方式。
[命题意图] 灵活使用模型法解决计数问题在这里以“□”来构造模型,利用数学建模进行数据处理和分析,从而使看不见摸不着的动态传球问题变得形象直观起来。
2.5白玉微瑕,美中不足
数据分析过程一定要注意各类限制条件。在排列数公式中,隐含条件 错解没有考虑到
错解没有考虑到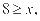
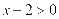 导致错误.忽视
导致错误.忽视 中的隐含条件而致误。
中的隐含条件而致误。
例5 不等式 的解集为__________.
的解集为__________.
[错解] 由排列数公式得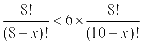 ,
,
化简得 ,解得
,解得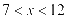 .因为
.因为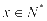 ,所以
,所以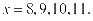
[正解] 由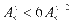 ,得
,得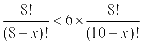 ,
,
化简得 ,解得
,解得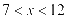 ①又
①又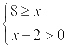 所以
所以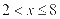 ,②
,②
由①②及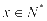 得
得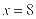 .
.
[命题意图] 解含排列数的方程或不等式时,要注意排列数 中,
中,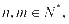 且
且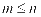 这些限制条件,要注意含排列数的方程和不等式中未知数的取值范围。
这些限制条件,要注意含排列数的方程和不等式中未知数的取值范围。
2.6相逢何必曾相识
解决排列、组合综合问题的策略:(1)解决排列、组合综合问题的一般思路是“先选后排”,也就是先把符合题意的元素都选出来,再对元素或位置进行排列。(2)解决排列、组合综合问题应注意:①元素是否有序是区分排列与组合的基本方法,无序的问题是组合问题,有序的问题是排列问题。②对于多个限制条件的复杂问题,应认真分析每个限制条件,然后再考虑是分类还是分步。
例6 从1,3,5,7,9中任取3个数字,从0,2,4,6,8中任取2个数字,一共可以组成多少个没有重复数字的五位偶数?
[解析] (1)五位数中不含数字0.
第1步,选出5个数字,共有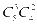 种选法。第2步,排成偶数,先排末位数,有
种选法。第2步,排成偶数,先排末位数,有 种排法,再排其他四位数字,有
种排法,再排其他四位数字,有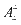 种排法。∴
种排法。∴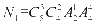 .
.
(2)五位数中含有数字0.
第1步,选出5个数字,共有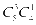 种选法。第2步,排顺序又可分为两小类:
种选法。第2步,排顺序又可分为两小类:
①末位排0,有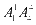 种排列方法;②末位不排0,这时末位数有
种排列方法;②末位不排0,这时末位数有 种选法,而因为零不能排在首位,所以首位有
种选法,而因为零不能排在首位,所以首位有 种排法,其余3个数字有
种排法,其余3个数字有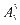 种排法。
种排法。
∴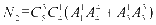 .∴符合条件的偶数的个数为
.∴符合条件的偶数的个数为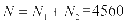 .
.
[命题意图] 讨论五位数中含“0”与否,是解答本题的关键。(1)末位排0与否,应分类讨论,否则极易出错。(2)本题是分类情况下的分步排列、组合问题,必须将所讨论的各种结果相加,否则会丢分。(3)解题过程中要注意分析特殊元素、特殊情况对结果的影响,并注意总结,避免因考虑问题不全面而丢分。
3总结和建议
相对于其他数学核心素养,数据分析是难度更大的、更高维度的核心素养。课堂教学要将培养学生的数据分析素养作为教学目标,教师通过精心设计题目引导学生思考“这类数据如何分析?哪种分析手段最好?分析中的注意事项是什么?”学生通过比较、联想、特殊化、类比进行强化,形成研究思路、找到研究方法,使其数据分析核心素养大幅度提高。
参考文献:
中华人民共和国教育部.普通高中数学课程标准(2017年版)[M].北京:人民教育出版社,2018.
张淑梅,何雅涵,保继光.高中数学核心素养的统计分析[J].课程•教材•教法,2017(10):51-54.
章建跃,程海奎.高中必修课中概率的教学设计和教学思考--兼谈“数学核心素养如何落地”[J].课程•教材•教法,2017(5):27-33.