云南电网有限责任公司德宏供电局
摘要:随着我国电动汽车数量的不断增加,严重影响了我国电力系统的稳定性,因此就需要对充电站的储能配置进行优化,在满足我国电动汽车充电需求的同时,实现充电站储能配置的最优化。鉴于此,本文通过建立双层储能优化配置模型,在保证充电站负荷最大的同时实现了充电站的收益最大化,并通过仿真优化分析,结果表明本文方案可以起到良好的削峰填谷作用,并进一步降低了充电站每年的购电成本。
关键词:电动汽车;充电站;储能系统;优化配置
0引言
随着我国经济的发展,我国对能源的需求不断增加,这进一步加剧了我国能源紧张问题,近些年来,我国大力发展新型能源以解决我国能源紧张问题,而电动汽车与传统汽车相比在节能减排方面有着巨大的优势。随着我国电动汽车的保有量逐年增加,汽车的充电需求也在急剧增长,但目前我国的相关配套设施还不够完善,还存在许多不足。现阶段,大规模电动汽车充电站在同时使用时对电力系统的稳定性造成严重影响。目前主要的解决措施是加装储能装置从而抵消大量电动汽车充电时所产生的峰谷,降低电网功率的波动,在为用户提供稳定电力资源的同时,减少对电力系统的影响。此外,充电站是电动汽车充电的重要载体,而站内充电负荷又是储能优化配置的重要指标,这直接影响着充电站储能配置的经济性。
1充电站储能优化配置规划模型
充电站内汽车的充电高峰与商业用电的高峰期基本吻合,根据站内电动汽车的负荷特征,并充分发挥储能系统的经济效益,本文依据峰谷电价制定了相应的储能运行策略,策略原则如下:一是对峰谷电价进行合理利用,从而提升充电站的经济效益;二是帮助配电网进行削峰填谷,减少电动汽车负荷对电网造成不利的影响。
充电站的储能优化配置,首先在建设初期需要考虑充电站的投资和建设成本,又要考虑站内储能系统的性能,通常情况下,储能系统的容量越大对电动汽车的负荷平抑效果就越好,但是这样会进一步增加充电站的建设成本。因此,充电站储能系统在建设时就要综合考虑充电站的各项建设成本,在保证收益最大化的同时,实现储能系统的优化运行。因此,本文采用双层结构对充电站的储能系统进行优化设计,从而实现充电站的最优配置。
1.1上层结构规划模型
上层规划的最终目的是实现充电站的年收益最大化,这就要考虑充电站建设时的各项成本和最终能够取得收益,本文对建设成本、维护成本、政府补贴以及运营收益4个影响因素进行分析,得到上层目标函数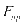 的表达式如下:
的表达式如下:
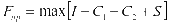 (1)
(1)
公式(1)中,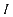 表示充电站每年可以取得的收益值,
表示充电站每年可以取得的收益值,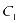 表示充电站的建设成本;
表示充电站的建设成本; 表示充电站建成后的每年维护成本值,
表示充电站建成后的每年维护成本值, 表示充电站建设时可以取得的政府补贴,这些影响因素的具体表达式如下:
表示充电站建设时可以取得的政府补贴,这些影响因素的具体表达式如下:
 (2)
(2)
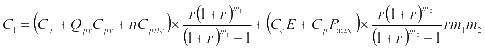 (3)
(3)
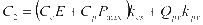 (4)
(4)
公式(2)表示充电站的年运营收益,其中包含充电站的充放电收益、电力公司的降峰奖励。公式中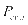 表示电动汽车的净负荷值,
表示电动汽车的净负荷值,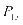 表示充电站的净负荷值,
表示充电站的净负荷值,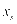 表示电动汽车的充电费用,
表示电动汽车的充电费用,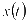 表示t时充电站购电的电价,
表示t时充电站购电的电价,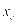 表示充电站高峰时段降峰所获得的电价补贴,
表示充电站高峰时段降峰所获得的电价补贴,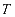 表示全天进行优化的段数,
表示全天进行优化的段数,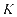 表示充电站充电的高峰时间段,由于受到站内负荷和光伏波动的影响,充电站的全年收益日取260个近似日,从而获取到充电站的运营利润年值。
表示充电站充电的高峰时间段,由于受到站内负荷和光伏波动的影响,充电站的全年收益日取260个近似日,从而获取到充电站的运营利润年值。
公式(3)表示充电站的整体建设成本,其中 表示充电站建设时的固定成本,
表示充电站建设时的固定成本, 表示光伏模块每单元的价格,
表示光伏模块每单元的价格, 表示充电站光伏配置的最大容量,
表示充电站光伏配置的最大容量,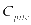 表示站内单个充电桩的价格,
表示站内单个充电桩的价格,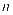 表示该充电站安装的充电站数量,
表示该充电站安装的充电站数量,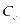 和
和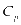 分别表示充电站储能电池每单位容量的价格和功率转换设备的单个价格,
分别表示充电站储能电池每单位容量的价格和功率转换设备的单个价格,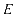 和
和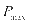 分别表示充电站储能系统的最大容量和储能系统的最大放电功率,
分别表示充电站储能系统的最大容量和储能系统的最大放电功率, 表示贴现率,
表示贴现率,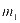 和
和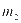 分别表示充电站光伏系统可使用的最大年限和储能系统可使用的最大年限。公式(4)表示充电站后续的维护成本,其中
分别表示充电站光伏系统可使用的最大年限和储能系统可使用的最大年限。公式(4)表示充电站后续的维护成本,其中 表示充电站储能系统每年的运行维护系数,
表示充电站储能系统每年的运行维护系数,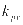 表示充电站光伏系统每年的运行维护系数。此外,充电站在建设时有政府的一次性建设补贴,为了便于后续计算本文将补贴金额设定为储能系统建设投入的30%。
表示充电站光伏系统每年的运行维护系数。此外,充电站在建设时有政府的一次性建设补贴,为了便于后续计算本文将补贴金额设定为储能系统建设投入的30%。
1.2下层结构规划模型
下层规划的目的是对充电站的充放功能进行优化,对充电站所造成的配电网峰谷进行抑制,这可以减少充电站的购电成本,下层规划模型的目标函数如下:一是实现全时段的配电网负荷曲线方差最小;二是实现充电站的购电成本最低,目标函数的表达式如下:
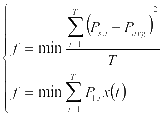 (5)
(5)
公式(5)中, 表示该区域的配电网在t时刻的负荷值,
表示该区域的配电网在t时刻的负荷值, 表示区域配电网一天内负荷曲线的平均取值。
表示区域配电网一天内负荷曲线的平均取值。
下层规划模型主要解决目标区域的优化问题,因此就需要将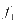 和
和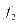 进行归一化处理,从而将较为复杂的双目标函数转化为单目标函数,其具体方式如下:
进行归一化处理,从而将较为复杂的双目标函数转化为单目标函数,其具体方式如下:
 (6)
(6)
公式(6)中,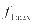 表示一天内配电网的最大方差值,
表示一天内配电网的最大方差值, 表示充电站一天内的最大购电成本,
表示充电站一天内的最大购电成本,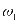 表示为
表示为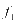 的权重系数,
的权重系数,
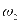 表示为
表示为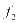 的权重系数,本文将区域配电网的负荷方差和日购电成本设置成相同的权重值,也就是
的权重系数,本文将区域配电网的负荷方差和日购电成本设置成相同的权重值,也就是
1.3约束条件
(1)功率平衡约束,其表达式如下:
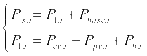 (7)
(7)
公式(7)中,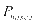 表示在t时刻商业区域的基础负荷,
表示在t时刻商业区域的基础负荷,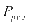 表示在t时刻光伏发电的数值,
表示在t时刻光伏发电的数值,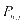 表示为在t时刻充电站储能系统的充放电功率,也就是说,当充电功率为负时,储能系统将会对外放电,当充电功率为正时,储能系统将处于充电状态。
表示为在t时刻充电站储能系统的充放电功率,也就是说,当充电功率为负时,储能系统将会对外放电,当充电功率为正时,储能系统将处于充电状态。
(2)储能系统的风电倍率约束
储能系统的充放倍率是充放电功率与电池容量的比值,如果充放电功率过大会损害电池的使用寿命,为了延长电池的使用年限,本文将充放电功率的上限设定为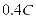 ,因此,储能系统的充放电倍率的表达式如下:
,因此,储能系统的充放电倍率的表达式如下:
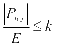 (8)
(8)
(3)充放电深度约束
为了避免过度充电或者过度放电而对电池的使用寿命造成影响,就必须保证储能系统运行在适合的负荷范围之内,其表达式如下:
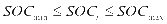 (9)
(9)
(4)负荷状态的连续性约束
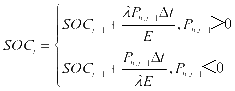 (10)
(10)
公式中,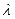 表示充电站储能系统的充放电效率。
表示充电站储能系统的充放电效率。
2优化分析
充电站的储能容量不同,储能的负荷优化能力也具有较大的差异,这会影响到充电站的最终收益,因此,本文对储能充电站0~1500kWh之间的储能配置进行仿真计算,从而了解充电站不同储能配置的收益情况,迭代周期为10KWh,具体计算结果如图1所示。因为粒子群算法在进行全局求解的过程中不可避免的会陷入局部最优,导致最终的计算结果呈现较大的波动性,因此本文对收益波动进行拟合计算,并以此为储能收益分布的参考值对充电站的最优容量进行配置。
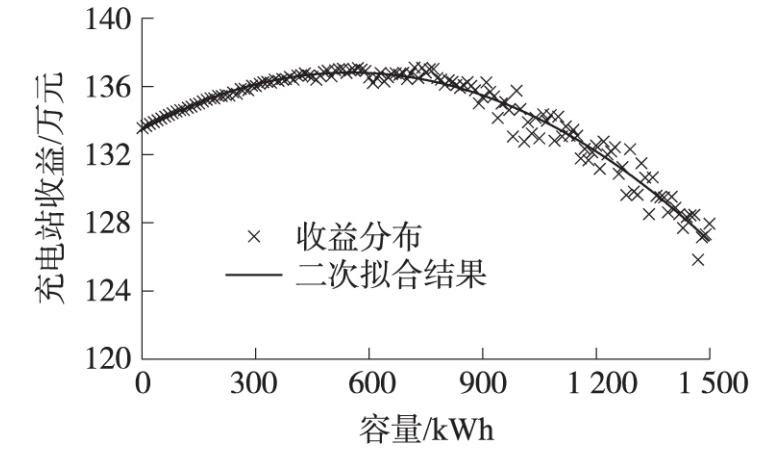
图1不同配置储能容量下的收益情况
从图1中可以看出,储能配置的容量越高充电站的收益就越好,但是到达580KWh附近时,随着储能容量的增加充电站的收益开始逐步降低。这是因为初始阶段储能系统可以很好的起到削峰作用,但随着充电站储能容量的增加,储能系统的配置成本会越来越高,而储能系统的收益已经无法弥补储能系统的配置成本,导致充电站的收益开始逐步降低,通过图5可知,当储能容量在580KWh附近时,充电站的收益可以达到最大化,也是最优的储能配置方案。
3结束语
电动汽车是我国新能源汽车未来重要的发展方向,而充电站又是电动汽车快速发展的前提和重要保障。但目前充电站的储能配置上依然存在许多不足,还需要不断的对其进行优化和配置。本文所提出的双层模型可以在一定程度上缓解充电站与电网之间的供需矛盾,并实现充电站整体经济效益的提升。
参考文献
[1]张怡, 唐蕾. 电动汽车充电站储能优化配置研究综述[J]. 电工电气, 2020(1):7.
[2]田东伟, 李默涵, 石进永,等. 基于能源聚合商的电动汽车充电站优化配置策略研究[J]. 电气应用, 2020, 39(9):8.
[3]张璐璐, 朱光云, 施寅跃,等. 电动汽车典型快充站优化运行配置方法[J]. 计算机系统应用, 2020.