合肥一六八玫瑰园学校东校区 安徽合肥 230601
摘要:牛顿运动定律是整个力学框架的基础,在很多模型中都有应用,其中板块模型是最为常见的应用之一。虽在某些板块模型中使用动量来更为方便。但在木板与桌面存在摩擦时我们大多需要用到最为基础、适用度最广的牛顿运动定律来解决。本文就六类基本情况进行讨论感受牛顿运动定律在板块模型中的应用。
关键词:板块模型 受力分析 牛顿第二定律 图象分析
为方便讨论,假设物块质量为m,木板质量为M,木板足够长。物块与木板之间的动摩擦因数为μ1,木板与地面之间的动摩擦因数为μ2.最大静摩擦力与滑动摩擦力相等。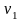 、
、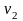 、
、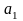 、
、 分别是物块、长木板的速度与加速度。
分别是物块、长木板的速度与加速度。
地面光滑,物块以一定初速度 冲上长木板,无其他外力作用。
冲上长木板,无其他外力作用。
受![]() 力分析如图1:(
力分析如图1:( )
)
m主动带M滑动。二者速度不同,相对滑动 。
。
运动分析:
m做初速度为 ,加速度为
,加速度为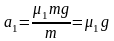 的匀减速直线运动;
的匀减速直线运动;
M![]() 做初速度为0,加速度为
做初速度为0,加速度为 的匀加速直线运动。
的匀加速直线运动。
当M与m速度相等时,二者一起运动。
3、 图象如图2:
图象如图2:
三角形面积S代表m相对M的运动距离。
因为木板足够长,所以一定会达到共速。
由系统动量守恒:
若木板长度为L,且L
假设需要时间t物块到达木板右端。根据匀变速运动性质结合位移关系:
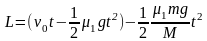
此后物块以 匀速直线运动,长木板以
匀速直线运动,长木板以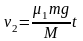 匀速直线运动。
匀速直线运动。
地面光滑,二者无初速度,有外力作用在长木板上。
【例1】如图3所示,质量为M足够长的木板静止在光滑地面,其中央放有一质量为m的物块,二者之间的动摩擦因数为μ1,最大静摩擦力等于滑动摩擦力。现作用在长木板上水平向右的力 。试分析物块和长木板的加速度
。试分析物块和长木板的加速度
受力分析如图3:( )
)
M带动m滑动。二者初速度一致,存在临界加速度问题。M由外力F提供动力,而m的加速度来源于M对m的摩擦。所以临界加速度由m决定。
运![]() 动分析:
动分析:
设二者共同运动,对整体有 。
。
而物块的最大加速度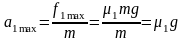
①当 ,即
,即 时,
时,
二者共同的加速度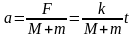
此时二者间的摩擦力 。
。
②当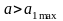 ,即
,即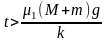 时,M与m间的摩擦超过最大静摩擦力,二者相对滑动,需要分开受力分析。
时,M与m间的摩擦超过最大静摩擦力,二者相对滑动,需要分开受力分析。
物块 ;木板
;木板 。
。
地面光滑,二者无初速度,有外力作用在物块上。
【变式】在例1中,如果外力 作用在物块上该如何分析?
作用在物块上该如何分析?
受力分析如图4:( )
)
m![]() 主动带动M滑动。M的加速度来源于二者间的静摩擦,故临界加速度由M决定。
主动带动M滑动。M的加速度来源于二者间的静摩擦,故临界加速度由M决定。
运动分析:
长木板的最大加速度
①当 ,即
,即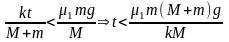 时,
时,
二者共同的加速度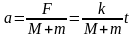
此时二者间的摩擦力 。
。
②当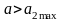 ,即
,即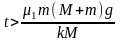 时,M与m间的摩擦超过最大静摩擦力,二者相对滑动:物块的加速度
时,M与m间的摩擦超过最大静摩擦力,二者相对滑动:物块的加速度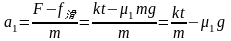 ;
;
木板的加速度 。
。
地面粗糙,物块以一定初速度 冲上长木板,无其他外力作用。
冲上长木板,无其他外力作用。
【![]() 例2】如图5所示,质量为M足够长的木板静止在粗糙水平地面,质量为m的物块以水平初速度
例2】如图5所示,质量为M足够长的木板静止在粗糙水平地面,质量为m的物块以水平初速度 从左侧冲上长木板,二者间动摩擦因数为
从左侧冲上长木板,二者间动摩擦因数为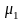 ,木板与地面间动摩擦因数为
,木板与地面间动摩擦因数为 ,最大静摩擦力等于滑动摩擦力。试讨论m与M的运动情况。
,最大静摩擦力等于滑动摩擦力。试讨论m与M的运动情况。
受力分析:
m运动带动M,M被动运动其速度不会超过m。
运动分析:
物块:m与M间速度不同,相对运动,所受摩擦力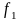 为滑动摩擦力。
为滑动摩擦力。
m做初速度为 ,加速度为
,加速度为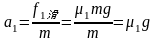 的匀减速直线运动。
的匀减速直线运动。
长木板:m对M的摩擦力 ,地面对M水平向左的摩擦力
,地面对M水平向左的摩擦力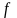 需要进行讨论。此处的最大静摩擦力为
需要进行讨论。此处的最大静摩擦力为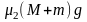 。
。
①若 ,木板静止,情况与木板固定一致。
,木板静止,情况与木板固定一致。
地面作用于长木板的摩擦力为静摩擦力 。
。
②若 ,木板滑动。
,木板滑动。
长木板:M做初速度为0,加速度为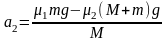 的匀加速直线运动。
的匀加速直线运动。
假设需要时间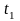 达到共同速度
达到共同速度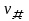 ,则:
,则: ,
,
物块相对长木板的位移为 。
。
注![]() 意:达到共速时是M与m间的摩擦力发生突变的时刻,此时M带动m减速,m是被动减速的。
意:达到共速时是M与m间的摩擦力发生突变的时刻,此时M带动m减速,m是被动减速的。
二者一起运动的加速度 ,
,
由于 ,
,
共同减速的加速度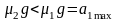 ,故二者一起以
,故二者一起以 减速至停止。
减速至停止。
第②种情况下二者 图象如图6。
图象如图6。
地面粗糙,二者无初速度,有外力作用在长木板上。
【![]() 例3】如图7所示,质量为M的足够长木板静止在粗糙水平面,其中央放有一质量为m的物块,二者之间的动摩擦因数为
例3】如图7所示,质量为M的足够长木板静止在粗糙水平面,其中央放有一质量为m的物块,二者之间的动摩擦因数为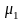 ,木板与地面的动摩擦因数为
,木板与地面的动摩擦因数为 ,最大静摩擦力等于滑动摩擦力。现作用在长木板上水平向右的力
,最大静摩擦力等于滑动摩擦力。现作用在长木板上水平向右的力 。试讨论m与M的运动情况。
。试讨论m与M的运动情况。
受力分析:
M带动m,共同运动的最大加速度由m决定。主要讨论两接触面的摩擦性质。
运动分析:
①当 时,即
时,即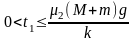 ,二者均静止,m与M间的摩擦力为0。
,二者均静止,m与M间的摩擦力为0。
②当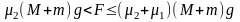 ,即
,即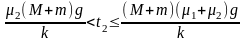 ,
,
若共同加速,则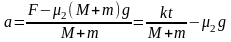
而 ,
,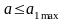 ,二者以相同加速度加速。
,二者以相同加速度加速。
M与m间的摩擦力
③当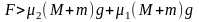 时,即
时,即 ,二者相对滑动。 物块:
,二者相对滑动。 物块: 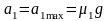
长木板: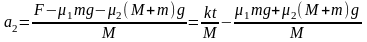 。
。
二者的 图象如图8所示。
图象如图8所示。
地![]()
![]()
面粗糙,二者无初速度,有外力作用在物块上。
【变式】现将 作用于物块m上,试讨论m与M的运动情况。
作用于物块m上,试讨论m与M的运动情况。
受![]() 力分析:
力分析:
m带动M,最大加速度由M决定。
运动分析:
最初F过小,二者都在摩擦的作用下静止,此时各个接触面的静摩擦力都等于F的大小。随着F 的不断增大,两个接触面的静摩擦都在增大,此时需要讨论哪个接触面先达到最大静摩擦力。
若 ,无论F多大,长木板均不可能运动起来,相当于长木板固定,物块滑动后地面给木板的摩擦
,无论F多大,长木板均不可能运动起来,相当于长木板固定,物块滑动后地面给木板的摩擦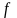 始终等于
始终等于 。
。
若 ,长木板与地面的摩擦先达到最大静摩擦力:
,长木板与地面的摩擦先达到最大静摩擦力:
①当 时,即
时,即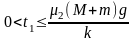 时,
时,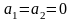 ,二者均静止。
,二者均静止。
②当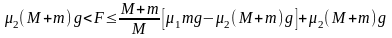 时,
时,
即 ,
,
二者共同运动的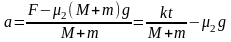 ,
,
未达到长木板的最大加速度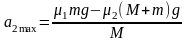 ,
,
故二者一起匀加速直线运动,其摩擦力为静摩擦力,可对M列式: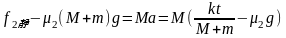
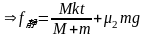
③当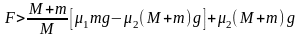 时,即
时,即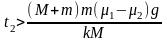 ,
,
二者相对滑动。
物块 ,长木板
,长木板 。
。
第(2)种情况下的 图象如图11.
图象如图11.
从六类板块模型的分析可以看出,问题的关键在于判断接触面是否相对运动,谁主动谁被动,共同加速的最大加速度由被动物体限制,共速是摩擦力突变的临界条件,然后结合牛顿第二定律分析每个过程中的运动情况,列式找出速度、加速度、时间、位移、相对位移等等之间的关系,从而解决问题。大致概括如下:
主动被动先分清,被动跟随不超越;相对运动要分清,动静摩擦很关键
速度不同为滑动,相对静止有限制;共速常伴摩擦变,受力分析要熟练。