例谈初中物理模型教学策略1

例谈初中物理 模型教学策略1

许宇伟

杭州师范大学附属未来科技城学校 浙江杭州 311100

【摘要】物理模型是一种重要的科学方法，它对复杂的问题的解决有独特的作用.在物理教学中运用图景模型、过程模型、理论模型来解决实际问题，有利于提高学生的物理能力.

【关键词】物理模型;教学策略

物理模型是重要的科学模型，也是物理学的重要研究方法.物理模型是人们对物理研究对象和过程的结果表达与解释.^[1] 模型是人们为了解决问题方便而研究出来的，模型的主要功能是问题研究与问题解决.

实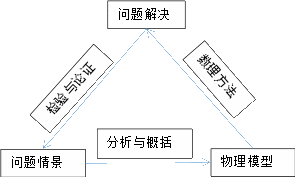 际问题往往很复杂，影响因子往往很多，要搞清问题的机制与原理.我们考虑问题时，可以对问题进行梳理与分类，对于具有同类性质的问题，我们可通过建立物理模型的方法来处理，再运用相关的数学与物理方法，达到问题解决，从而来检验与论证问题.在解决物理问题时，通常考虑矛盾的主要方面，暂时忽略次要因素，通过对问题的抽象与概括的来解决问题，三者关系如图1所示.问题研究的关键是哪些因素必须重点考虑，哪些因素可以忽略.因此，在物理教学中培养学生对物理模型的建构、理解与应用能力，是培养学生物理核心素养的重要方面.

图1

一、重视直观表象，构建图景模型

物理研究的是物质世界，物质世界从微观粒子到宏观宇宙，每一个事物都是相当复杂的.模型一个重要特征是形象性，我们可以物理图景模型形象表达物理学现象及规律.在物理教学中，可以采取由物理现象→物理模型→物理新情景→问题解决教学范式，不断加强形象的实际情景与抽象的物理规律的关系，提高学习的效率.图景模型是抽象思维向形象思维过渡的桥梁，能把研究对象及其变化过程生动地展示出来.

【案例1】宏观与微观世界的模型表达

在宏观领域，人们为了表达这个宏大的宇宙大世界，就采取了图景模型的方法来表达，利于人们理解.希腊科学家托勒密在亚里士多德等前人基础上创立了地心说（图1）；哥白尼否定了地心说，建立了日心说（图2），认为太阳是宇宙的中心，地球和行星是绕太阳做圆周运动的，月球围绕着地球转.乔治·加莫夫提出了热大爆炸宇宙论模型（图3），宇宙最初开始于高温高密度的原始物质，大爆炸后宇宙不断膨胀，温度下降，宇宙物质逐渐凝聚出现星云、星系、恒星、行星.随着科学技术的不断发展，表达形式也愈抽象，而物理模型的直观可理解性的意义也就愈大，人们的认识愈深入.

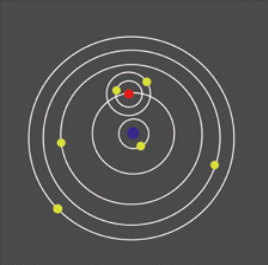
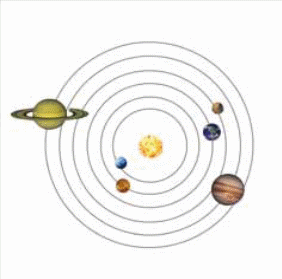
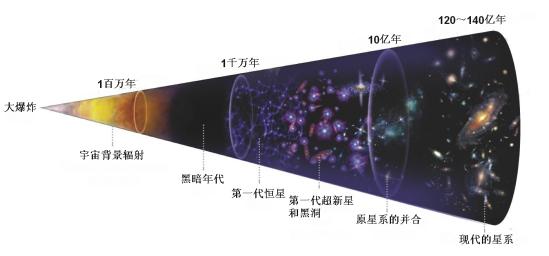
图1 地心说模型 图2 日心说模型 图3 大爆炸宇宙论模型

同样的，人们对于微观世界的研究，为了把抽象的微观世界表达出来，常常把微观的事物可视化，把抽象的东西直观化，便于人们的理解.例如，道尔顿把原子模型建构为实心的模型（图4），认为原子是组成物质的基本粒子，它们是坚实的、不可再分的实心球；汤姆生为了说明原子结构模型，把原子比喻为枣糕模型或西瓜模型（图5），认为电子像面包里的葡萄干那样镶嵌在其中，原子是一个平均分布着正电荷的粒子，其中镶嵌着许多电子，正负电荷相互中和形成了中性原子；卢瑟福提出“行星绕太阳”的原子结构模型（图6），认为原子的中心有一个带正电荷的核，几乎集中了原子的全部质量，电子围绕着原子核不同的轨道运转，就象行星环绕太阳运转一样；波尔提出分层模型（图7），认为电子在原子核外空间的按能量高低分别在一定轨道上绕核做高速的圆周运动.这些图景模型很好地帮助我们理解微观世界的物理现象及规律.

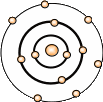
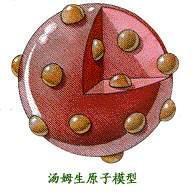
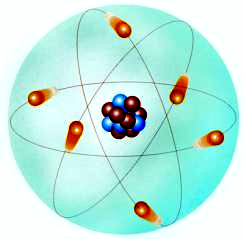
图4 实心模型 图5 枣糕模型 图6 行星绕太阳模型 图7分层模型

物理学发展史是一部不断提出新物理模型、不断完善模型，甚至替换旧物理模型的历史.在不断演替过程中，科学理论、思维方法、以及表征客观原型的工具和方式等，也在不断地丰富和发展.^[2]

物理教材经教材专家选择与编辑，内容典型而又简约，具有高度抽象性、概括性.教师不能只是读一下教材内容或者播放一下课件，因为这样高度抽象与概括性的物理概念与规律，对于学生来说很难理解，必须经过教师处理形成形象化的图景模型来表达知识的内涵特征，化抽象为具体，让学生好接受，并将科学方法和科学思想寓于模型中，促进学生打开思维的闸门，让学生自己悟出物理原理.

二、显示变量关系，构建函数模型

借助数学表征能加深对物理现象及其变化规律的理解.函数模型不仅在数学中经常使用，物理学科也经常运用函数模型.函数模型能简明扼要地描述变量关系，化繁为简，不仅能反映不同物理变量的关系，而且也能促进学生对物理规律的理解.^[3]函数模型是形象思维向抽象思维转转变的桥梁，它能帮助我们建立起研究对象及其变化过程的逻辑关系.有利于提高学生严谨的思维能力和学生的洞察能力.

【 案例】密度计的刻度探究

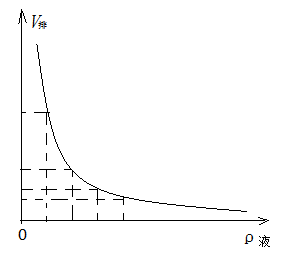
密度计是测量液体密度的仪器，它是一根密封的玻璃仪器，上部细长,下部短粗，下端装有铅粒使重心降低，使它能竖直地漂浮在液体中，密度计上段有刻度，刻度上疏下密，刻度值上小下大.学生对于这个刻度特点，往往靠记靠背.为了使学生能理解这样刻度的原因，我们不妨利用函数模型来进行教学.

图8

当密度计竖直地漂浮在液体中时,密度计自身重力等于浮力，即G＝ρ_液gV_排 ，ρ_液＝G/(gV_排)，由于密度计自身重力G 以及重力加速度g不变,因此，液体密度ρ与V_排 成反比,即属于反比例函数（图8），ρ越大则V_排越小,密度计浸在液体中越浅,因此，密度计的刻度值是上小下大的.当密度计测量不同液体时，ρ₁＝G/(gV_排1)，ρ₂＝G/(gV_排2)，则ρ₁—ρ₂=G（V_排2—V_排1）/（gV_排2V_排1），由于密度计相邻刻度线对应的ρ₁、ρ₂相差不大，所以，可以近似认为V _排1≈V_排2= V_排 ，因此，ρ₁—ρ₂≈GSΔh/gV²_排,其中S是上部小玻璃管的横截面积，Δh是刻度之间的间距，结合上述函数图像，并结合此式可知，对确定的密度变化来说，V_排越大，Δh也越大.所以，密度计的刻度上密下疏.

不同特征的信息对大脑中枢产生不同的作用，直观形象图景模型能促使学生引起形象思维，形成空间概念.左脑善于抽象思维，利于抽象概括和演绎，而右脑善于空间直观思维.图景模型能较好地结合文字信息和图形信息，能交替刺激左右大脑，使左、右半脑交替活动，学生大脑思维品质可以得到较好的训练.

三、体现实验探究，构建过程模型

面对具体复杂的客观事物，都离不开对物理问题的分析.为了便于分析和研究，对实际问题进行科学的抽象，抓住问题的本质特征，略去次要因素，问题得到解决，在教学中，通过对物理模型设计思想及建模过程的探究性学习，学生能逐渐学会运用抽象思维的方法处理实际问题，有利于提高学生的思维能力，并掌握科学方法，能培养学生对复杂问题进行分析、辨别主要因素和次要因素的能力.

【 案例】研究电流与电阻的关系

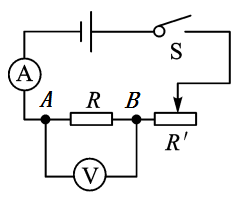
欧姆定律是非常重要的内容，几乎所有老师都会通过实验的方法来探究电流与电阻的关系，许多老师往往走过场，测得三组数据就可以得出结论，但是，这样的话不能使学生理解电阻变化引起电阻变化的内在规律，不利于学生深入理解欧姆定律的本质.在实验中，要保持电压不变，改变电阻大小，研究电流与电阻之间的关系，本实验的关键是如何控制R两端的电压不变. 图9

例如，如图9，实验仪器为电源电压恒为3V，电流表量程0-0.6A、电压表量程0-3V，滑动变阻器“50Ω 1A”，定值电阻5Ω、10Ω、15Ω、20Ω，等等.

为了测得多组数据，探究电流与电阻的关系，控制A、B之间的电压为2V；第一次，选择的电阻5Ω，调节滑动变阻器，使电压表示数为2V，测得电流值为0.4A，第二次，电阻更换为10Ω时，教师宜先让学生想一想，此时滑动变阻器阻值怎样变才能使A、B间的电压仍为2V？在实践中发现，许多学生更多的是随意的猜测，实际上是不知道怎样操作，这也是本实验中的一个重点与难点所在.实验中务必让学生自己动手操作，回顾并建立串联电路中分压的模型：U₁/U₂=R₁/R₂，即在串联电路中，电压之比等电阻之比，可以简单说成“大阻分大压，小阻分小压”，便于记忆与理解，从而突破教学的难点.继续更换电阻为15Ω、20Ω，让学生继续探究如何控制电压2V不变，反复操作之后，获得有关数据，并画出反比例函数的图像，同时可得到“电压一定时，电流与电阻成反比”的结论（过程建模）.

在此之后，不妨进一步探究：“在本电路中，在A、B之间允许的电阻阻值范围.”这个难度显然更大，可以适当引导学生，关注电流表与滑动变阻器的允许的电流范围可知，电路最大电流为0.6A，定值电阻R_小=U/I=2V/0.6A=3.3A，而变阻器的最大阻值为50Ω，根据U₁/U₂=R₁/R₂，可得R_大=100Ω，在本电路中，在A、B之间允许的电阻阻值范围为3.3Ω-100Ω.对于串联电路的分压模型U₁/U₂=R₁/R₂进一步得到操练，深刻理解欧姆定律的内涵.

过程模型就是把具体物理过程理想化、纯粹化后所抽象出来的一种物理过程.在进行科学探究时，要引导再现已经感知过的物理模型，同时，以先前获得的物理模型为依据，经过猜测、判断、推理、论证，逐渐形成自己的研究方法，形成独立分析与探究能力，使探究过程更为深刻，掌握物理的本质特性.在本实验探究中，我们控制A、B两端的电压一定，寻找电流与电阻的关系，就是一种“纯粹化”处理的一种方式，比如在本实验中，我们把电流表与电压表就作为理想电表进行使用，不考虑其内阻的变化影响，同时，把两节电池的内阻也予以忽略.让学生感知各种事物的运动变化过程虽然是复杂的，我们可以通过主次分析，把次要因素予以忽略，保留过程中的主要因素，这样就得到了过程理想模型.

四、突出思维关联，构建理论模型

法国学者阿雷指出：科学的基本活动就是探索和制定模型.对于物理问题的解决过程中，是一个建立物理模型、选择模型方法的过程，能正确地使用物理模型解决物理问题，是中学生必备科学素养.所以，在物理教学中要重视对学生物理模型建构能力的培养，提高学生的思维能力.通过某种诱因，把记忆表象系统有关表象联系在一起形成思维，而结构性模型方法就是促进各种表象的联系，提高学生的想象能力与分析推理能力，有助于把学过的知识连一条线或者知识网络.

【 案例4】运用数学理论模型解决实际问题

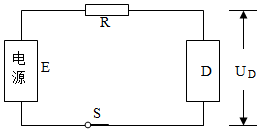
如图10，E为电压可调的电源，R为定值电阻，D为起稳压作用的电子元件，即在一定条件下，D两端电压U_D不变，则下列电路中的电流I、电阻R消耗的电功率P随电源电压U_总变化关系的四个图像中，可能正确的是（　　）. 图10

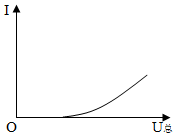
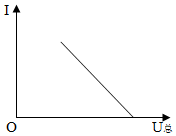
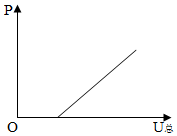
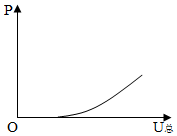
A B C D

观察四个图像可以分为两类，第一类是电流与电压的关系，第二类是电功率与电压的关系，通过类比、分析认识所研究问题的本质内容，建立合理的物理模型.在串联电路中，R两端电压为U_R=U_总-U_D，所以I=（U_总−U_D）/R,其中U_D、R都为定值，因此，电流I与U_总是一次函数关系，其中斜率K=1/R ＞0；而A图不是一次函数关系图，B图像的斜率K＜1，不符合该函数.R的电功率P=U ²/R=（U_总-U_D）²/R，因R和U_D为定值，可知，P与U_总的变化关系为二次函数关系，图像应该为抛物线，C图像为一次函数，D图像可能是抛物线.
本题学生得分率很低，主要原因是找不到正确解题的方法.教师可以引导学生寻找数学理论模型，来寻找函数图像.本题是考查串联电路的电流与电压关系，以及对欧姆和电功率公式的灵活运用，解题的关键是找到I、U_总以及R消耗的电功率P与U_总的变化的函数关系式，根据函数的理论模型来解决实际问题，体现了理论模型在物理中的运用.其解题过程中，运用思维方法来分析、归纳、构建与问题相适合的物理模型.

模型是思维的结果，物理模型的构建与运用，就是对物理情景分析、抽象和解释的一种思维方法，物理模型的应用、分析是具有思维的灵活性、深刻性、广阔性等特性的.物理模型来源于客观实际，反过来可以解决实际问题.因此，在教学中，把学习构建出来的物理模型与现实问题、现象联系起来，进行应用理解，运用具体的方法，有效提高学生的思维能力.

参考文献：

[1]曹宝龙.物理模型的建构与教学建议[J].物理教学探讨，2016（5）：1-5.

[2]谭会.中学物理模型教学设计的理论与实践研究[D].华东师范大学，硕士学位论文，2009.5.

[3]陈苍鹏.例谈地理模型模型教学策略[J].地理教学，2017（20）：42-45.

基金项目：2017年浙江省规划课题《初中科学实验创新活动与科学核心素养培养的实践研究》阶段成果(项目编号 ：2017SC008)

1