河南省濮阳市第一高级中学 457000
求动点的轨迹方程问题是高考的热点问题,难度较大,根据近几年全国卷的相关题目的得分情况开看,得分率普遍较低.求动点轨迹方程的关键是要仔细审题,分析已知条件和动点轨迹的特点,然后将动点满足的条件用动点坐标来表示,化简要注意等价变形,并要考虑一些特殊点是否适合方程.
求动点的轨迹方程的一般步骤:在平面直角坐标系中,设动点 ,根据题目条件,得出横坐标x与纵坐标y的关系式,即为动点的轨迹方程.简化来说,核心步骤是建系、设点、列式、代人、化简、检验.
,根据题目条件,得出横坐标x与纵坐标y的关系式,即为动点的轨迹方程.简化来说,核心步骤是建系、设点、列式、代人、化简、检验.
一、待定系数法
当已知曲线的形状时,利用待定系数法,设出曲线方程,根据已知条件,求出未知数.此类题目一般比较简单.
例1.与椭圆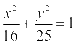 共焦点,且过点
共焦点,且过点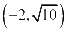 的双曲线方程为( )
的双曲线方程为( )
A.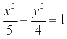 B.
B. C.
C.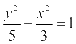 D.
D.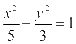
【解析】由题得椭圆的焦点为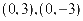 ,所以双曲线的焦点为
,所以双曲线的焦点为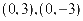 ,
,
设双曲线的方程为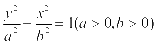 ,所以
,所以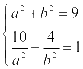 ,解之得
,解之得
所以双曲线的方程为 .故选:B.
.故选:B.
【答案】B.
二、定义法
定义法往往是根据课本中椭圆、双曲线与抛物线的定义,需要利用数形结合思想,挖掘位置关系,研究动点满足的几何特征,从题目的已知条件中提取出相关定义进行求解.
例2.动圆M与圆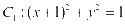 外切,与圆
外切,与圆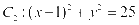 内切,则动圆圆心M的轨迹方程是__________.
内切,则动圆圆心M的轨迹方程是__________.
【来源】安徽省淮南市2019-2020学年高二上学期期末数学(文)试题
【解析】设动圆的圆心为: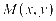 ,半径为
,半径为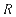 ,
,
动圆与圆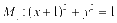 外切,与圆
外切,与圆 内切,
内切,
所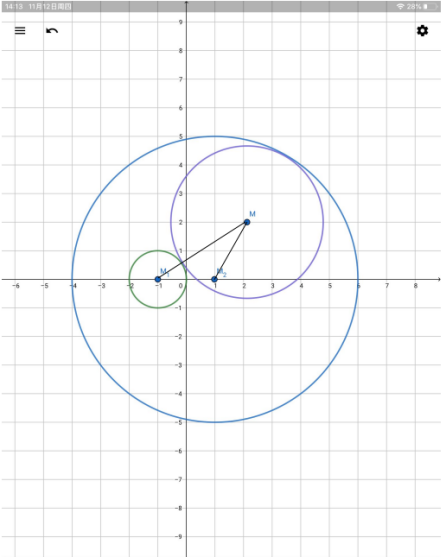 以
以 ,
,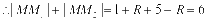 ,
,
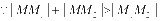 ,因此该动圆是以原点为中心,焦
,因此该动圆是以原点为中心,焦
点在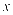 轴上的椭圆,且
轴上的椭圆,且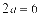 ,
,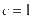 ,解得
,解得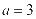 ,
,
∴ ,
,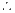 椭圆的方程为:
椭圆的方程为: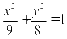 .
.
【答案】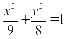 .
.
名师点拨:如果动圆与两个相互内含的定圆的位置关系为一个内切,一个外切,那么动圆圆心的轨迹为椭圆.同样可得:
1.如果动圆与两个相离的定圆(圆M、圆N)的位置关系为与某一个外切,某一个内切,那么动圆的圆心的轨迹为双曲线;
2.如果动圆与两个相离的定圆(圆M、圆N)的位置关系为与圆M外切,与圆N内切(与圆M内切,与圆N外切),那么动圆的圆心的轨迹为双曲线的一支;
3.如果动圆与两个相离的定圆的位置关系为同时外切或内切,那么动圆的圆心的轨迹为双曲线的一支.
4.如果动圆与一个定圆和一条直线同时相切(直线与定圆不相切),那么动圆的圆心的轨迹为抛物线;
5.如果动圆与一个定圆和一条直线同时相切(直线与定圆相切),那么动圆的圆心的轨迹为抛物线或一条射线.
三、直译法
根据题意中动点的几何关系,将其转化为动点坐标 的关系式,化简后即为动点P的轨迹方程,在将关系式进行变形和化简的过程中,一定要注意是否等价.
的关系式,化简后即为动点P的轨迹方程,在将关系式进行变形和化简的过程中,一定要注意是否等价.
例3..动点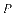 与定点
与定点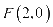 的距离和它到定直线
的距离和它到定直线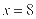 的距离的比是
的距离的比是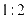 ,则动点
,则动点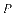 的轨迹方程是___________.
的轨迹方程是___________.
【来源】广东省阳江市第三中学2019-2020学年高二上学期第二次月考试题
【解析】设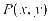 ,则
,则 ,化简得:
,化简得: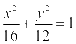 .
.
【答案】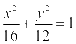 .
.
名师点拨:已知平面内某动点P到定点F的距离与到定直线l的距离之比为e,当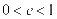 时,动点P的轨迹为椭圆;当
时,动点P的轨迹为椭圆;当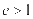 时,动点P的轨迹为双曲线;当
时,动点P的轨迹为双曲线;当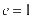 时,动点P的轨迹为抛物线.此为圆锥曲线的第二定义.
时,动点P的轨迹为抛物线.此为圆锥曲线的第二定义.
例4.已知两点 、
、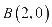 ,直线
,直线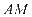 、
、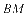 相交于点
相交于点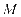 ,且这两条直线的斜率之积为
,且这两条直线的斜率之积为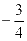 ,则点
,则点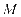 的轨迹方程为________.
的轨迹方程为________.
【来源】河南省南阳市第一中学2019-2020学年高二上学期第四次月考数学(理)试题
【解析】设点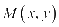 ,由直线
,由直线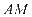 、
、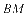 的斜率之积为
的斜率之积为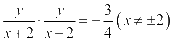 ,
,
整理得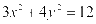 ,即
,即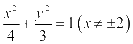 ,
,
因此,点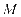 的轨迹方程为
的轨迹方程为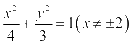 .
.
【答案】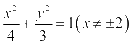 .
.
名师点拨:已知平面内某动点P到两定点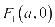 ,
,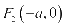 的斜率的乘积等于常数
的斜率的乘积等于常数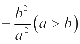 ,则该动点的轨迹为椭圆;动点P到两定点
,则该动点的轨迹为椭圆;动点P到两定点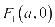 ,
,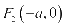 的斜率的乘积等于常数
的斜率的乘积等于常数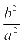 ,则该动点的轨迹为抛物线.此为圆锥曲线的第三定义.
,则该动点的轨迹为抛物线.此为圆锥曲线的第三定义.
四、相关点法(涉及点差)
根据题目中的条件,无法直接列出动点的相关关系式,但是所研究的动点本身不是主动
运动,而是受另一动点运动的牵制,即动点是随着另一相关点的运动而运动,一般需要将两个点的坐标都设出来,用动点的坐标表示相关点的坐标,代入相关点所满足的等式,便可得到动点的轨迹方程.
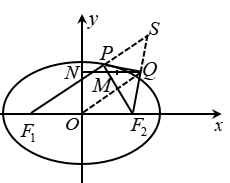
例5.已知椭圆 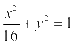 的左右焦点为
的左右焦点为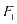 、
、 ,点
,点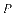 为椭圆上任意一点,过
为椭圆上任意一点,过 作
作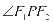 的外角平分线的垂线,垂足为点
的外角平分线的垂线,垂足为点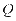 ,过点
,过点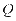 作
作 轴的垂线,垂足为
轴的垂线,垂足为 ,线段
,线段 的中点为
的中点为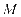 ,则点
,则点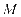 的轨迹方程为___________.
的轨迹方程为___________.
【 来源】邯郸市大名一中2020-2021学年高二上学期10月月考题
来源】邯郸市大名一中2020-2021学年高二上学期10月月考题
【解析】如图,延长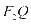 交
交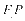 的延长线于
的延长线于 ,连接
,连接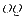 .
.
因为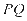 为
为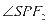 的平分线且
的平分线且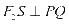 ,
,
故 为等腰三角形且
为等腰三角形且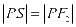 ,
,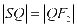 ,
,
所以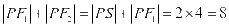 .
.
在 中,因为
中,因为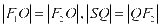 ,所以
,所以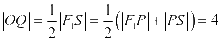 ,
,
故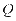 的轨迹方程为:
的轨迹方程为: .令
.令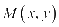 ,
,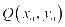 ,则
,则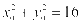 ,
,
因为线段 的中点为
的中点为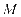 ,所以
,所以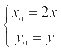 ,所以
,所以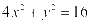 ,即
,即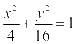 .
.
【答案】
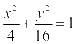 .
.
五、参数法
有些题目很难直接找出动点的横、纵坐标,如果中间借助中间参数,如斜率、变角等,可以很容易地使动点的横、纵坐标之间建立联系,消去参数,即得动点的轨迹方程.消参时一定要注意参数的取值范围对方程中的x和y的范围的影响.
例6.平面直角坐标系中,已知两点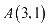 ,
,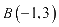 ,若点
,若点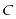 满足
满足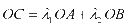 (
(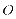 为原点),其中
为原点),其中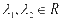 ,且
,且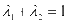 ,则点
,则点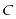 的轨迹是( )
的轨迹是( )
A.直线 B.椭圆 C.圆 D.双曲线
【来源】陕西省渭南市临渭区2019-2020学年高一下学期期末数学试题
【解析】设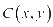 ,则
,则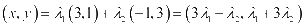
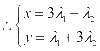 ,解得:
,解得: ,
,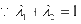 ,
,
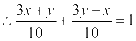 ,整理得:
,整理得: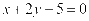 ,
,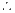 点
点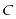 的轨迹是直线.
的轨迹是直线.
【答案】A.
六、交轨法
如果动点是两条动曲线的交点,即动点的坐标同时满足两条曲线方程,选出一个适当的参数,求出两条动曲线的方程或动点坐标适合的含参数的等式,再消去参数,即得所求动点轨迹的方程,需注意动点的取值范围.
例7.已知过点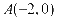 的直线与
的直线与 相交于点
相交于点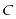 ,过点
,过点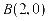 的直线与
的直线与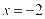 相交于点
相交于点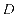 ,若直线
,若直线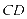 与圆
与圆 相切,则直线
相切,则直线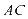 与
与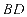 的交点
的交点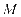 的轨迹方程为__________.
的轨迹方程为__________.
【来源】江苏省南通市如皋中学2020届高三创新班下学期高考冲刺模拟(三)数学试题
【解析】设直线AC,BD的斜率分别为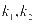 ,则直线AC,BD的方程分别为:
,则直线AC,BD的方程分别为: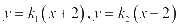 ,据此可得:
,据此可得: ,
,
则: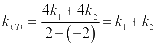 ,直线CD的方程为:
,直线CD的方程为: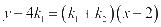 ,
,
整理可得: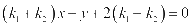 ,直线与圆相切,则:
,直线与圆相切,则: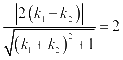 ,
,
据此可得: ,由于:
,由于: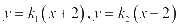 ,
,
两式相乘可得: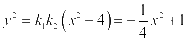 ,
,
即直线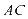 与
与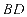 的交点
的交点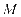 的轨迹方程为
的轨迹方程为 .
.
名师点拨:求轨迹方程,要注意曲线上的点与方程的解是一一对应关系,检验应从两个方面进行:一是方程的化简是否是同解变形,消参的途径灵活多变;二是是否符合实际意义,注意轨迹上特殊点对轨迹的“完备性与纯粹性”的影响.
注明:本文系2021年度河南省基础教育教学研究项目《新课标下数学思想方法在高中物理中的应用与研究》(课题编号 JCJYB210609028)的研究成果。