初中数学创设情境引入新课五法

初中数学创设情境引入新课五法

葛琳

四川省攀枝花市第七中高级中学校

摘 要：所谓创设问题情境，就是在教材内容和学生求知心理之间制造一种“不协调”，把学生引入一种与问题有关的情境的过程。

关键词：创设情境；自然引入；注意问题

所谓创设问题情境，就是在教材内容和学生求知心理之间制造一种“不协调”，把学生引入一种与问题有关的情境的过程。这一过程将激发学生强烈的求知欲望，给他们以强大的探究动力。教师认真钻研教材，了解学生的实际情况，从学生的学习兴趣出发，创设贴近学生生活，且带有激励性和挑战性的情境，在平时的教学中很有必要。创设情境的方法有很多，我在这里把平时教学中比较实用的几种方法总结如下：

一、结合数学与生活和生产密切联系的实例创设情境，从而引入新课

《数学课程标准》指出：“……强调从学生已有的生活经验出发，让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程……”数学来源于生活，在我们身边有许多数学问题，如银行利率问题、商品打折问题、修建水泵站问题等，所以教师要善于从现实生活和生产中挖掘数学素材，并结合课堂教学知识设计学生感兴趣的情境。这样不仅能够加深学生对知识的理解，激发学生的求知欲。

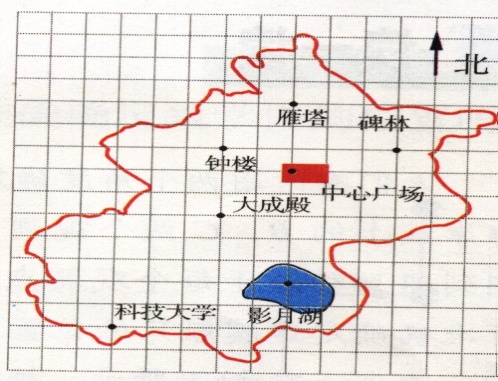
如在讲授《平面直角坐标系》时，可设计这样的情境：

（幻灯展示）上图是某市旅游景点的平面示意图。

1．你能说出各个景点的位置的吗？

2．“大成殿”在“中心广场”的西、南各多少格？碑林在“中心广场”的东、北各多少格？

3．“科技大学”在“大成殿”的西、南各多少格？“影月湖”在“科技大学”的东、北各多少格？

然后教师引导：同学们根据这个问题的启示，你可以怎样表示你在教室中的位置？学生在热烈的讨论交流中自然进入新课的学习。

二、联系旧知识，利用悬念创设情境引入新课

建构主义教学论明确提出：“复杂的学习领域应针对学习者先前的经验和学习者的兴趣，去激发学习者学习的积极性，学习才是主动的。”教材中的许多概念、解题方法等往往具有内部的联系。对于这些知识的教学，教师可以引导学生研究已经学过的知识的属性，在深刻理解和巩固旧知识的基础上，让学生结合已有知识，解决当前问题，使学生产生困惑，创设出欲罢不能的期待情境，从而调动学生思维的积极性，引入新课的学习。

如教授《合并同类项》时，设计了这样的情景：

复习提问，引入新课：

1.什么叫做同类项？

2.判断下列说法是否正确：

(1) 是同类项. （ ） (2) 是同类项.（ ）

(3) 是同类项.（ ） (4) 是同类项.（ ）

3.用幻灯片展示一些群居动物的图片。

教师在点评的基础上进而阐述：人以群居，物以类聚。你能运用乘法分配律把几个同类项合并成一项吗？

这个情境创设，在巩固“双基”的情况下，又很好的起到了铺垫作用,通过设置悬念引入新课。

三、设计学生活动创设情境 ，在积极的氛围中引入新课

在平时的教学中，把学生熟悉的、感兴趣的事物与教材相结合，设计成操作性、直观性强的游戏活动，引导学生主动参与，动手去制作、实践，让学生在轻松的游戏活动中，体验知识的发生发展，从而进入新课的学习。

如在教授《一定摸到红球吗？》时，可这样创设情境：

在课前准备了3个纸箱，这三个纸箱只有面对学生的那面是透明的，正上方凿了一个洞，能放进手去摸球。其中第一个纸箱放了10个红球，第二个纸箱放了5个红球，5个白球，第三个纸箱放了10个白球。然后让四名不知情的学生来做摸球游戏，其中3人摸球，另一人作记录，然后把三名学生摸纸箱的结果公布。提问：

1.谁一定摸到红球？为什么？

2.谁可能摸到红球？为什么？

3.谁肯定摸不到红球？为什么？

4.多摸几次试试看，还是你认为的那样吗？

这样学生在体会游戏的乐趣的同时，又能感知必然事件、不可能事件以及不确定事件的意义，进而水到渠成的引入新课的学习。

四、通过介绍数学史实、小故事创设情境，轻松引入新课

教学中，结合教材内容适当的补充一些名人轶事，介绍一些数学史实、小故事，让学生在感悟中，产生浓厚的学习兴趣，激发学习热情，从而引入新课。

在教学《勾股定理》第一课时时，有这样的数学小故事：

数学家毕达哥拉斯有一次应邀参加一位政要的餐会，这位主人豪华宫殿般的餐厅铺着正方形的美丽的大理石地砖，由于大餐迟迟不上桌，这些饥肠辘辘的贵宾们颇有怨言。等待之余，这位善于观察和理解的数学家毕达哥拉斯却凝视脚下这些排列规则、美丽的方形磁砖，但他不只是欣赏磁砖的美丽，而是想到它们和“数”之间的关系，于是拿了画笔并且蹲在地板上，选了一块磁砖以它的对角线 为边画了一个正方形，他发现这个正方形的面积恰好等于两块磁砖的面积和。他很好奇，于是再以两块磁砖拼成的矩形的对角线为边作另一个正方形，他发现这个正方形的面积等于5块磁砖的面积，也就是以矩形的两边长为边作两个正方形的面积之和。至此毕达哥拉斯作了大胆的假设： 任何直角三角形，其斜边的平方恰好等于另两边平方之和。那一餐饭，这位古希腊数学大师的视线一直都没有离开地面。

通过这样一个小故事，其一是让学生了解数学家探究勾股定理的过程，从而对本节课的学习内容有一个初步感知；其二是让学生体会到数学家在探索一个问题时，是多么的专心，让学生受到了深刻的思想教育。于是，教师在学生情绪高涨时自然引入新课的学习。

五、借助学科间的整合创设情境引入新课

数学与很多学科联系紧密，教师要抓住数学是基础学科这一特性，整合各学科资源，挖掘与数学教材相关的一些其他学科知识，结合教学内容创设恰当的情境，从而引入新课。

如某老师教授《一次函数》时的情境创设：

有关函数的问题在我们日常生活中随处可见，如弹簧秤有自然长度，在弹性限度内，随着所挂物体的重量的增加，弹簧的长度相应的会拉长，那么所挂物体的重量与弹簧的长度之间就存在某种关系，究竟是什么样的关系，请看：

某弹簧的自然长度为3厘米，在弹性限度内，所挂物体的质量x每增加1千克、弹簧长度y增加0.5厘米。

（1）计算所挂物体的质量分别为1千克、2千克、3千克、4千克、5千克时弹簧的长度，并填入下表：

（2）你能写出y与x之间的关系式吗？

这里利用学生生活中熟悉的弹簧秤，结合物理中的一些力学知识，让学生体会函数是刻画解决一些实际问题的重要模型，进而引入新课。

在平时的教学中，教师要善于结合教材内容，结合学生实际，创设恰当、有效的教学情境，使一堂课有一个良好的开端。

参考书目：

1.《全日制义务教育数学课程标准（实验稿）》

2.周秀峰 昌国良 《谈新课标下初中数学课堂情境创设》 数学教学通讯