数学模型教学在中考复习中的方法与策略

数学模型教学在中考复习中的方法与策略

周福志

南宁市江南区吴圩镇初级中学 530225

摘要：高效的教学模式是保证中考复习水平的前提，通过数学模型教学的创新应用，梳理中考复习思路，并帮助学生掌握复习方法并提高数学模型教学水平，可实现数学中考复习水平的进一步提升。以学生的实际情况为导向，对数学模型教学的实践应用展开讨论，并以“中点数学模型”为案例，分析数学模型教学在中考复习中的应用策略，旨在提高中考复习水平。

关键词：数学模型；中考复习；教学方法

引言：数学模型教学的应用，则是以中考复习需求为导向，对数学模型教学方法以及教学互动等进行优化，提高中考复习水平。以教师指导为基础，通过数学模型教学工作的创新，以学生探究、讨论等为中心，在对课堂结构以及教学模式等进行优化的基础上，可实现数学模型教学的综合发展水平提升^[1]。

1数学模型

数学模型的构建与发展，则是在数学思维拓展的视角下，通过收集、整理、归纳各类数学问题，并通过数学模型解决中考的相关数学问题。在创建数学模型的过程中，则需要通过数学模型培养学生的数学逻辑思维^[2]。数学模型可以针对三角形、四边形的线段关系、三角形构造与计算等进行整合，在模型统计与分析的基础上，运用数理逻辑的方式，通过数学语言建构模型，达到解决数学问题的目的^[3]。

2数学模型教学在中考复习中的应用方法

在中考复习中，常见数学题中存在等量关系，所以，可以通过建立方程模型、不等式模型、直角三角模型等方式，对中考复习过程进行优化，提高学生的数学解题能力。例如，在对距离、高度、水坝等应用型问题进行计算中，可以通过直角三角形模型搭建的方式，对数学问题进行计算，可提高数学模型在中考习题中的应用水平。例如，A、B之间有一条河，从A到B需要通过D、C两个点，并按照ADCB的顺序到达目的地。新建EF，可直接沿直线AB从A地到达B地，BC的距离为11km，∠A为45°，∠B为37°，DC与AB平行，计算AB两点之间少走了多少路程？

在对这一数学问题进行计算中，则可以建立直角三角形模型，并对AB相交点以及构建的平行四边形进行设计，通过数学计算，可获得结果。

通过数学模型解决中考复习问题，则需要从变量关系、等量关系的角度进行计算，运用数学相关知识进行解决，在利用数学函数模型的基础上，可提高学生的中考复习水平。初中数学教材中编制地大部分应用型问题，为了体现理论联系实际的复习原则，普遍存在分量过轻、内容陈旧、范围过窄等缺点，因此，在数学建模的过程中，结合复习内容，将数学模型融入到数学问题分析中，在丰富学生视野的同时，可增强学生的数学应用意识。

从数学建模分析的角度，深入生活联系实际，用生活中的数学问题，提高学生的数学模型应用意识，在新课标背景下，将数学问题转化为数学模型，并充分利用学生生活中的事件，提高学生对数学模型的理解能力。在渗透建模思想下，可提高学生的解题能力。

以社会热点问题为背景，编拟应用型问题，在利用数学建模的过程中，则需要从学生数学逻辑思维、数学问题处理过程等角度进行教育拓展，根据中考阶段的数学复习内容，对不同数学模型的实际应用进行调整，将数学建模与数学教学有机结合在一起，并注意学生数学建模能力的培养，提高学生在中考中的应变能力。

例如，倍长中线或类中线构造全等三角形，则是通过模型进行计算，在遇到中线或者中点时，可以尝试利用倍长中线，构造全等三角形，并对已知条件中的线段进行转化。在进行计算中，其实际情况如下：

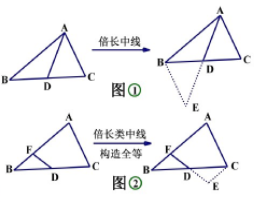
如图①，AD为△ABC的中线，延长AD至点E，促使DE=AD，可以证明△ADC＝△EDB（SAS）

如图②，D是BC中点，延长FD至点E，促使DE=FD，可以证明△FDB=△FDC（SAS）

在利用数学模型解决中考复习问题的过程中，则是从数学探究以及知识训练的角度，对数学模型的实践应用过程进行完善，并通过自主探索与合作交流的方式，实现学生的数学模型思维提升。在利用数学模型的过程中，注重激发学生的学习热情以及兴趣，并通过列举典型、说明意义以及明确目的，促使学生可以感受到学习、探索的需要，结合中考复习要求，对知识讲解以及数学模型体验等进行完善，提高中考复习的教学效果及效率。

专题内容的设计则需要遵循教学的认知规律以及学生的心理发展规律，对不同数学模型之间的关系、构建方式等进行优化，在对数学模型进行优化下，可实现中考复习水平的进一步提升。针对几何模型、三角形模型等在数学应用题中的应用进行分析，在寻找问题切入点后，构建模型方程，并对数学模型的计算过程、中点模型的辅助线应用等进行拓展，可提高数学模型教学的综合水平。在利用数学模型后，可总结模型规律，并对数学模型的逻辑关系、数学处理过程、问题分析等进行优化，

3数学模型教学在中考复习中的应用策略——以“中点数学模型”数学模型为例

在对中点数学模型的搭建进行研究中，其中包含任意三角形或四边形中点或中点有关的线段、出现两个或三个中点考虑三角形中线定理等模型，在对中点数学模型的实际应用进行研究中，则需要从辅助线应用的角度，对中点数学模型进行搭建，提高中点数学模型的中考复习水平。例如，△OAB、△OCD为等腰直角三角形，∠AOB=∠COD=90°，点C在OA边上，点D在OB边上，连接AD，BC，M为线段AD的中点，求证，OM⊥BC。

在对上述问题进行数学模型搭建中，则是从数学逻辑关系的角度，对数学知识内容进行调整，提高数据分析与计算效率。利用中点数学模型，可以对上述逻辑关系进行分析，建立数学模型，达到解题的目的。中点数学模型的搭建与应用，则需要通过数学模型的搭建，对模型性质、逻辑关系等进行优化，并通过数学模型分类，要求学生了解并掌握数学模型的应用，提高中考复习效率。

结语：数学模型教学创新中，突出数学模型的独特性以及创新性，并根据中考复习的渐进性以及特征，对数学模型教学方式、学生的逻辑思维等进行优化，在数学模型拓展与调整下，提高数学模型教学的综合发展水平。

参考文献

[1]张亚楠. 试论新课改下中学数学建模教学策略[J]. 黑龙江科学,2021,12(01):124-125.

[2]王茜,高丽. 如何发展初中生的数学模型思想[J]. 现代交际,2021(03):167-169.

[3]李洪明. 如何有效开展初中数学几何教学[J]. 科学大众(科学教育),2019(05):14.