内嵌空间钢桁架双钢板剪力墙性能分析

内嵌空间钢桁架双钢板剪力墙性能分析

陈子龙，闫文龙，高璐，张文丽，王继浩

郑州大学 450000

摘要：本文利用 ABAQUS 有限元软件模拟了地震荷载作用下的内嵌空间钢桁架双钢板剪力墙受力过程,提取数据并得到精准化分析结果。对比分析了L形、T形以及圆环形等不同桁架截面形式的滞回曲线及骨架曲线，研究其力学性能，并对其设计选型提出建议。

关键词:有限元分析；内嵌空间钢桁架；滞回曲线

1.引言

随着钢板剪力墙的发展与应用，其良好的受力性能很快得到了人们的重视。双钢板组合剪力墙也因其组合性能，使内嵌材料多一重约束，面内面都具有更好的稳定性，且承载能力与抗侧性能都有显著提高而被广泛应用于结构安全性能要求高或恶劣环境条件下的高层建筑中。再者，空间钢桁架为格构式几何不变体系，造型多样、传力明确，大强度小变形、具有较好的稳定性，杆件以轴向受力为主，可充分利用材料的抗拉压性能。鉴于空间钢桁架自重轻、承载力大的承力特点，将其与双钢板剪力墙通过合适的节点构造进行组合设计。在郑州大学大学生创新创业项目训练计划的资助下，本文进行了内嵌空间钢桁架的装配式双钢板剪力墙（SPSW）力学性能的数值模拟研究。

2.有限元模型建立

2.1模型概况

本文通过有限元分析综合研究了SPSW受内嵌空间桁架约束的力学行为。模型中各部件参数如下：梁的横截面为200×200×12×8 mm（截面高度×截面宽度×腹板厚度×翼缘厚度）；钢板的高度和厚度分别为2400mm和6 mm。钢板的宽厚比（宽度/高度）为400。使用的桁架直径为8mm，厚度为2mm，有限元模型如图1所示。 各种桁架构件的相关参数参照表1。

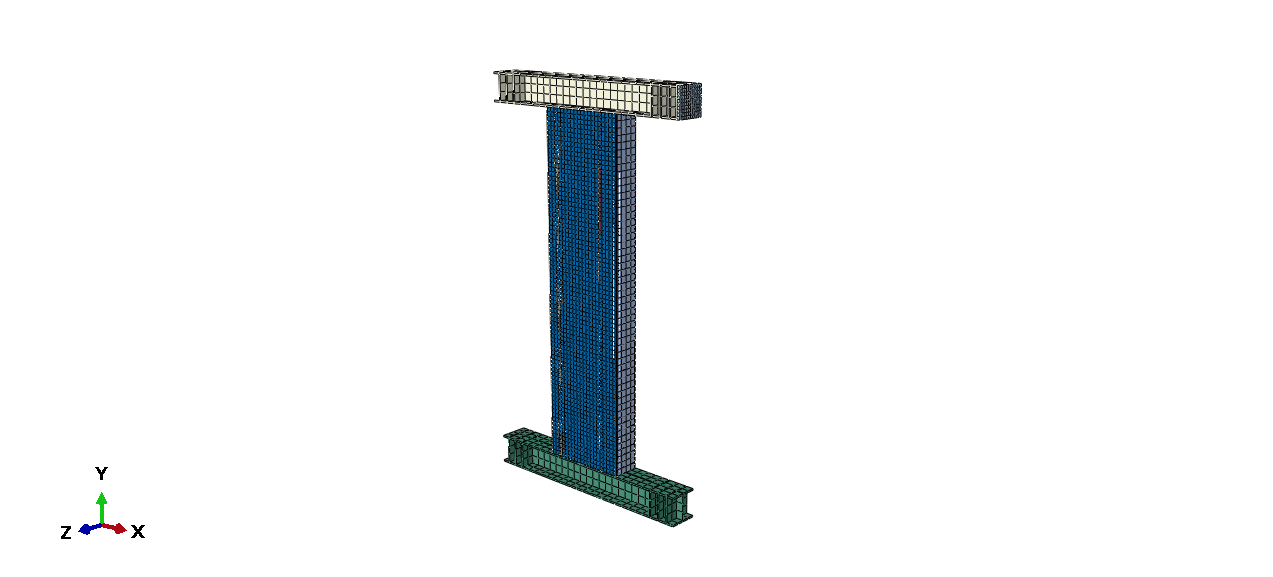
图1（a）模型整体图 图1（b）模型桁架图

表1 桁架参数表

2.2模型建立

参照文献^[1]的建模方法建立数值分析模型。通过八节点三维实体线性压缩积分单元（C3D8R）模拟试件中的单元选择，所有钢板，地梁、加载梁、槽钢与角钢，如图1所示。试件中桁架采用B31。材料采用Q235B钢，其参数如图2，然后对整体模型进行坐标计算，创建地梁、加载梁等部件，模型在分析的过程中需要设置一个分析步。为了使模拟过程和实验过程有很好的吻合程度，用绑定（Tie）命令实现墙与承载梁，墙与地梁之间以及墙内各个杆件之间的连接。

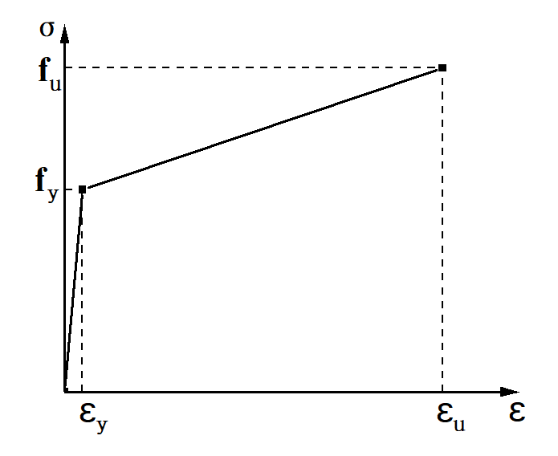
图2钢材应力-应变关系曲线图

2.3模型加载制度

根据美国 AISC 抗震规范^[2]的规定，本试验采用位移控制的加载方式，以层间位移角作为控制因素，如图3所示。

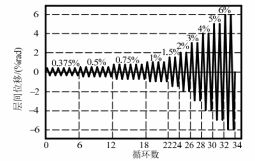
图3加载制度

3.有限元结果分析

3.1滞回曲线对比分析

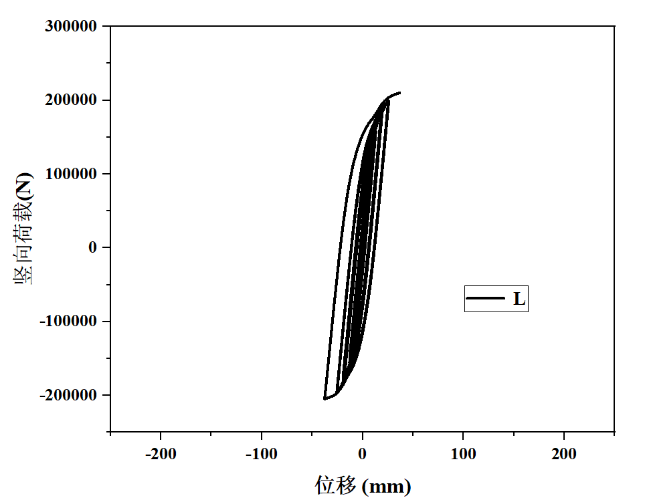
图4（a）W-1的滞回曲线

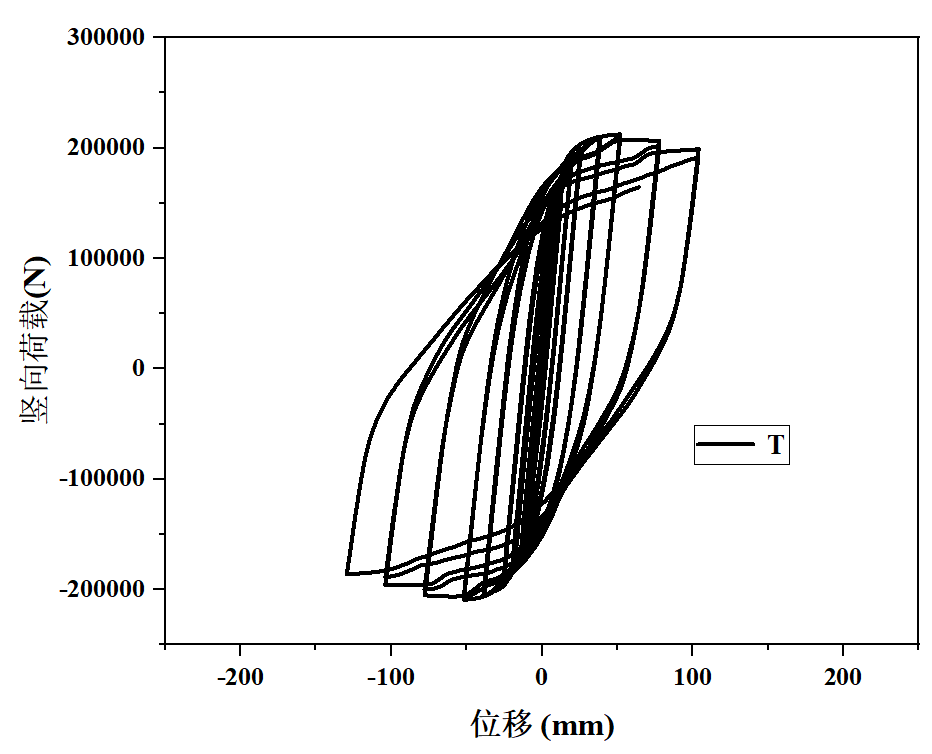
图4（b）W-2的滞回曲线

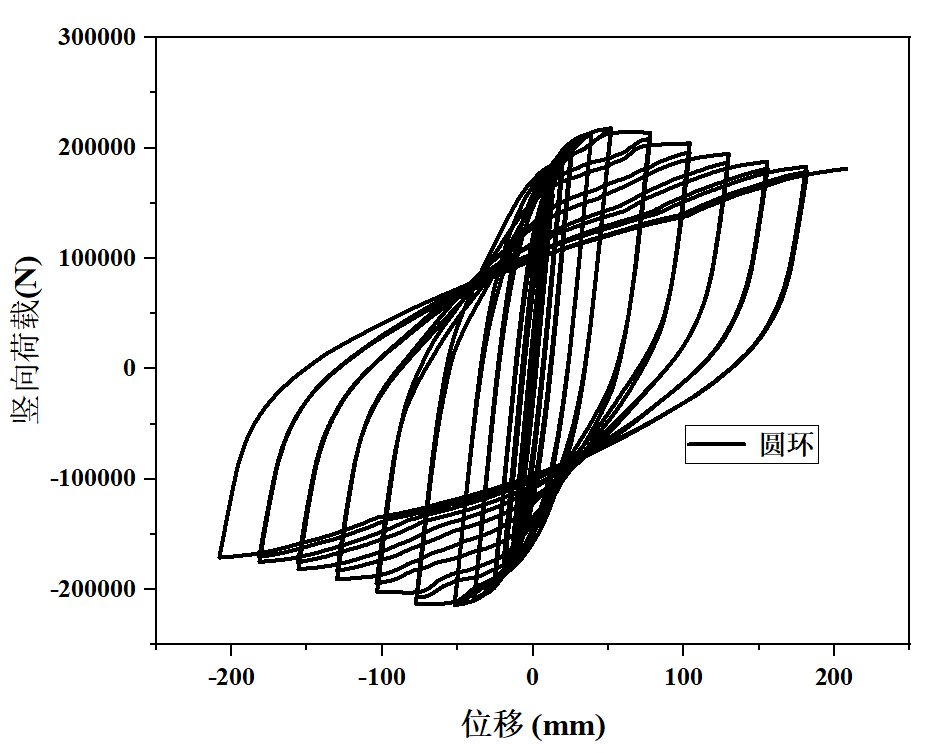
图4（c）W-3的滞回曲线

对三类（W-1表示L型截面的内嵌空间桁架，W-2表示T型截面的空间桁架，W-3表示圆环形截面的桁架形式）不同横截面形式的桁架组合而成的双钢板剪力墙的滞回曲线进行分析，W-1结构破坏迅速，此时的结构承载力较低。W-2 并未出现捏缩现象，且曲线比较扁平。W-3出现了捏缩现象，且其曲线饱满、发散程度高。

3.2骨架曲线

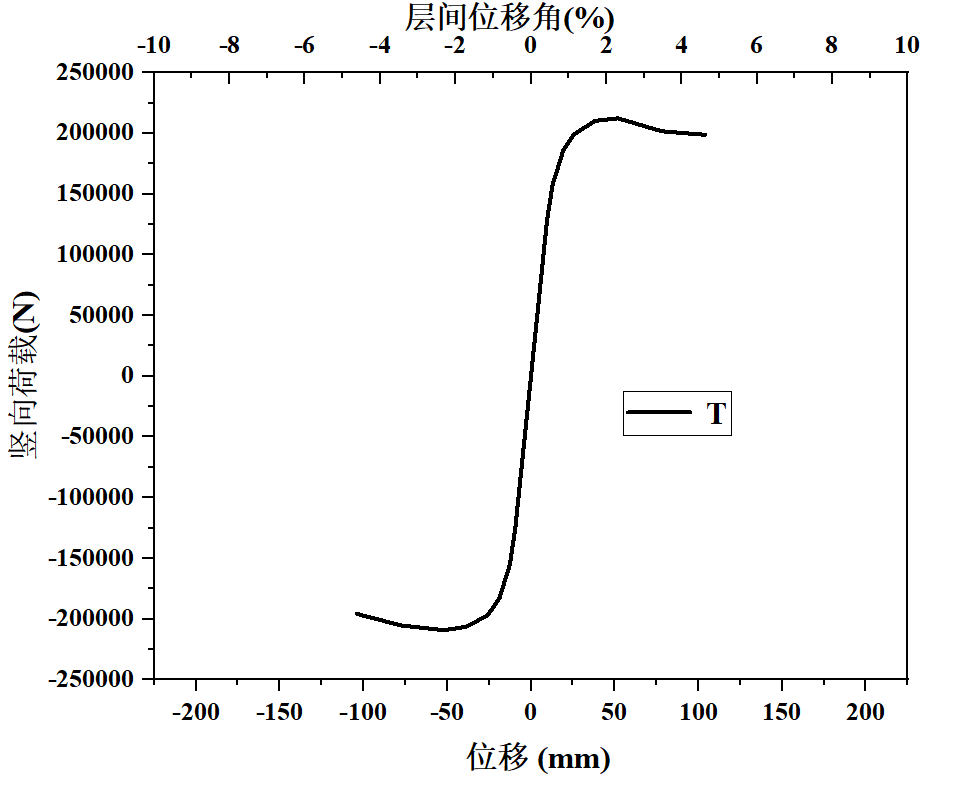
图5（a）W-2的骨架曲线

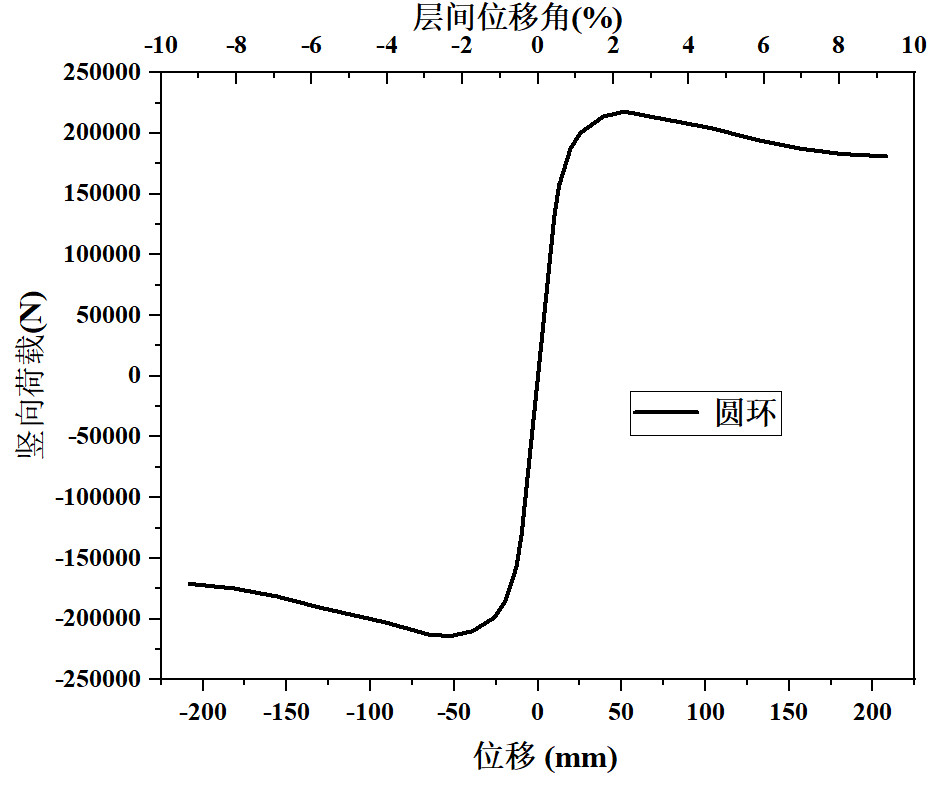
图5（b）W-3的骨架曲线

由于W-1的滞回曲线表明W-1试件受力性能不佳，所以不予讨论。对比W-2与W-3，可以发现，当取层间位移角为2%时，W-2的最大承载力大于W-3的最大承载力，承载性能好。由最大位移可知，W-3试件的延性比W-2的延性好，所以综上所述，W-3整体性能由于W-2。

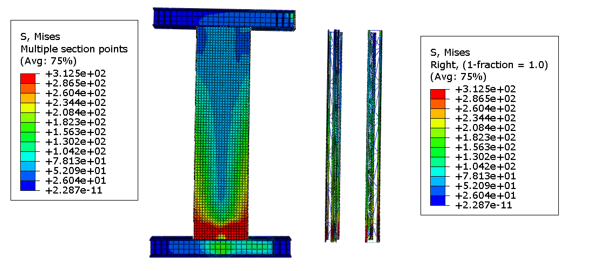
图6（a）试件W-1结果图

图6（b）试件W-2结果图

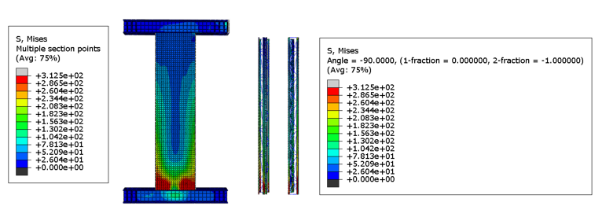
图6（c）试件W-3结果图

4.结论

在内嵌空间桁架的双钢板剪力墙中，截面形式是对承载力与抗侧性能影响较大的一个因素。本文重点讨论了当桁架截面为常用的L形、T形以及圆环形截面时，内嵌空间桁架的剪力墙的受力性能，从而为工程中设计选型提出建议。

（1）当桁架截面为圆环形时，内嵌空间桁架的承载力最高，且延性最好，充分发挥空间桁架的力学性能。

（2）桁架截面为T形与L形时的承载力均没有圆环形时的高，其原因为T形与L形是非双对称截面，而L形是无对称截面，杆件的各个方向受力不均匀，导致空间桁架结构受力性能较差。

参考文献：

[1] 张爱林，张 勋，刘学春，王 琦,.钢框架-装配式两边连接薄钢板剪力墙抗震性能试验研究[A].工程力学，2018，35（9），54-72

(北京工业大学建筑工程学院，北京 100124)

[2] AISC/ANSI 341―10, Seismic provisions for structural

steel buildings [S]. Chicago: American Institute of Steel

Construction, 2010: 56.