上海对外经贸大学
【摘要】随着经济的不断的发展和社会财富的不断积累,财产价值日趋集中,使保险人承担的责任越来越大,也使保险人所面临的经营风险越来越大。为达到稳定经营,保持财务稳定的目的,需要将超出偿付能力以外的责任转移,这时候就需要再保险。最优再保险就是当今所追求的一种双赢状态,再保险的关键在于选择再保险的方式。保险人进行再保险的目的不同,自然也存在着不同的最优标准。
本文从效用的角度运用效用理论分析保险最优再保险的问题。再保险的优化准则其中之一就是期望效用最大,我们首先对问题的提出背景进行了简要的分析。其次,我们选取期望效用作为衡量标准,用效用来表示决策人对损失或收益的反映程度,以达到最大期望效用作为最优尺度。在此基础上,证明了赔付率超赔再保险是在效用理论下的最优再保险方案,并就此讨论了在保费不确定情况下,赔付率超赔再保险的最优自留额确定问题。
【关键字】最优再保险 效用理论 再保险 效用函数 期望效用 最优自留额
1.引言
随着对外贸易和商品经济的不断发展和完善,现代交通的日益发达,经济中心城市逐渐形成,社会财富日益积累和集中,使得一次事故可能造成的物质财富损失和人身损伤程度加深。在保险人承担的保单中不可避免的存在此类小概率事件,例如煤矿的开采,石油的开发,大型客机,核电站等此类保险的保额额巨大,小概率事件一旦发生,所造成的损失,是无法由一个或多个保险公司全部承担下来的。保险公司通过再保险将自身承担的风险向其他保险公司进行转移,与此同时需要向转入的保险公司缴纳再保险费,造成了利润的流出。保险人应如何合理地在风险和利润间进行取舍,便产生了对再保险优化问题的研究。保险公司通过再保险进行更为彻底地风险分化,不仅能进一步扩大保险人的承保能力,也有利于维持经营的稳定性。而再保险自留额的确定和再保险方式的选择是再保险优化研究的核心问题。
2.1最优再保险形式
假定原保险人的风险态度由效用函数 表示。用效用来衡量保险人对各种再保险方式的偏好,以效用达到最大作为最优标准。在此优化标准下,停止损失再保险是最优的。
表示。用效用来衡量保险人对各种再保险方式的偏好,以效用达到最大作为最优标准。在此优化标准下,停止损失再保险是最优的。
假定保险人制定分保计划时有:
保险组合的初始准备金为 ;
;
保险人为风险厌恶型,即其效用函数满足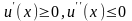 ;
;
保险人在一观察期内(一般为一年)的总损失额为 ,其中再保人承担的损失为
,其中再保人承担的损失为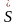 ,且
,且 <
<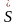 <
< ;
;
再保险费为 ,其中
,其中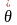 为安全附加系数,为方便讨论,省去费用和正常利润。
为安全附加系数,为方便讨论,省去费用和正常利润。
则停止损失再保险使期望效用达到最大,即

 ,
,


其中 由方程
由方程 决定。
决定。
证明:假设保险组合的保费为P,期初收取。由于保险人是风险厌恶型,其效用函数是凹函数,所以对任意的两点 有
有 。
。
假定用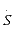 表示满足假设条件的任意一种再保险方式,则有:
表示满足假设条件的任意一种再保险方式,则有:
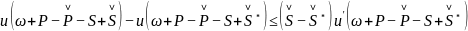
(1.1)
接下来证明
 (1.2)
(1.2)
分三种情况进行讨论:
情况1: ,此时显然式(4-2)两边相等;
,此时显然式(4-2)两边相等;
情况2: ,由于
,由于 ,所以
,所以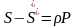 ,故式(4-2)成立。
,故式(4-2)成立。
情况3: ,由于
,由于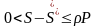 ,所以
,所以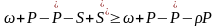 。因为
。因为 ,所以
,所以 为单调递减函数,于是
为单调递减函数,于是
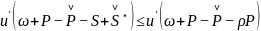 (1.3)
(1.3)
因此式(4-2)也成立。
两边同取数学期望,得
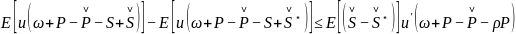
依照前面的假设, ,所以
,所以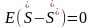 ,于是
,于是
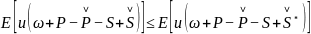
可见,停止损失再保险是期望效用达到最大意义下的最优。
2.2确定停止损失再保险的最优自留额
上一节的讨论中,分保费用 为一确定数值,得出了效用理论下停止损失再保险为最优再保险形式的结论。本节将讨论分保费不确定情况下,效用理论下的停止损失再保险的最优自留额模型。为使证明过程更为清楚,将对符号进行重新假设。
为一确定数值,得出了效用理论下停止损失再保险为最优再保险形式的结论。本节将讨论分保费不确定情况下,效用理论下的停止损失再保险的最优自留额模型。为使证明过程更为清楚,将对符号进行重新假设。
1.投保人的总损失额为连续随机变量X,其分布函数和密度函数分别为F(X)和f(x)。其中 ,F(I)=1;
,F(I)=1;
2.期初收取总保费V,原保险的分保费用为P,自留额为0 表示最优自留额;
由期望效用理论,最优自留额将使原保险人在分保后的最终财富值的期望效用达到最大。分保后,原保险人的财富值为 ,由此我们可以得出停止损失再保险下的最优自留额
,由此我们可以得出停止损失再保险下的最优自留额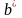 的数理模型:
的数理模型:
为求得最优自留额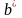 ,我们利用导数的方法,对目标函数进行求解。
,我们利用导数的方法,对目标函数进行求解。
由上述模型:

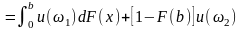



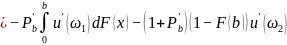 (2.1)
(2.1) (2.2)
(2.2)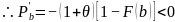 (2.3)
(2.3)
将(2.2),(2.3)代入(2.1)中得:

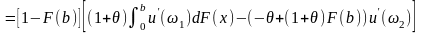
最优自留额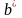 由方程
由方程 决定。
决定。
3.结论
近几年来,关于再保险的最优化研究不断增加,风头正盛,而效用理论下的最优再保险研究也是其中的较为热门研究课题。在我国财产保险公司中,由于法定准备金的长期存在,再保险并没有得到重视,以至于没有得到进一步的发展。而随着经济的不断发展,再保险扮演着越来越重要的角色,受到越来越多的关注。在再保险业务的经营过程中,通过再保险的优化安排,将进一步的分散风险并进行转移,使保险公司承担更小的风险或承受更小的损失,达到维持财务稳定、保证公司偿付能力、稳定经营的目的。本文详细论述了效用理论下的最优再保险模型,得出了效用理论下的最优再保险形式和不定保费下的最优自留额模型,并利用效用函数的相关数理特征证明了停止损失再保险是效用理论下的最优再保险。
本文证明了停止损失再保险是效用理论下的最优再保险形式,此外通过导数的方法,得出了在保费不定情况下,停止损失再保险的最优自留额的数理模型。
【参考文献】
胡祥,张连增.基于期望效用函数最大化的最优再保险策略[J].统计与决策,2017(08):50-52.
王霞. 一般保费原则下的帕累托最优再保险策略的研究[D].山东师范大学,2017.
刘红丽. 基于保险人和再保险人双方的最优再保险研究[D].山东师范大学,2017.
王真. 再保险中最优化策略的研究[D].郑州大学,2014.
何远兰. 最优停止损失再保险研究[D].暨南大学,2010.
曹玉松.效用函数下的最优再保险策略[J].许昌学院学报,2010,29(02):4-6.
颜丽华. 效用理论下的再保险研究[D].燕山大学,2010.
曹玉松. 最优再保险的研究[D].浙江大学,2006.