基于数学思想方法的等腰三角形易错问题归纳

周春艳 张颖 黎琳俐

重庆三峡学院 重庆 万州 404121

摘要：通过对等腰三角形易错题型的归纳，一方面帮助学生避开解题陷阱；另一方面明确教师应该引导学生将数学思想方法贯穿于理解题意到反思解题的整个数学解题过程，达到“得鱼”与“得渔”的双重效果，帮助学生养成良好的数学思考方式.

关键词：等腰三角形；易错问题；数学思想方法

教师在教学过程中不仅要引导学生解题思路，更要引导学生总结概括数学思想方法. 学生通过解决一个数学问题掌握其中蕴含的数学思想方法后，从而解决这一类型的数学问题，达到触类旁通的效果. 在数学解题过程中渗透数学思想方法，还有利于培养学生的数学思维，使思维更敏捷、更具条理性. 等腰三角形作为一个特殊图形，有其特殊的性质，在初中几何问题中占有非常重要的地位^[1]，但由于思维不全面、思维惯性、性质理解不深刻等原因，学生往往陷入一些陷阱，现将等腰三角形中常见的易错题型归纳如下.

1 有关边的易错题型

例1：已知等腰三角形一边长为 ，一边长为 . 求此等腰三角形的周长.

易错原因：一是未考虑两种情况，二是虽然考虑了两种情况，但易忽略形成三角形所必须满足的三边关系. 这里需要引导学生体会其中蕴含的分类讨论思想：（1）先从腰和底边两个角度进行分类；（2）再从三角形任意两边之和大于第三边进行检验.

例2：已知等腰三角形底边长为 ，一腰上的中线将此等腰三角形分成周长之差为 的两部分，求此等腰三角形的周长.

易错点：（1）题目中只表明一腰上的中线将三角形周长分为周长之差为 的两部分，但没有明确给出哪一部分的长度之和更大，因此很多学生只考虑了一种情况. （2）忘记检验所得结果是否满足三角形成立时所必须满足的三边关系，导致第二种情况的结果不完善，没有给出这种情况成立时对应的取值范围.

2 有关角的易错题型

例3：已知等腰三角形一角度数为 ，求该等腰三角形的底角度数.

易错原因：只考虑了此角为等腰三角形的底角的情况，忽略了此角为等腰三角形的顶角的情况. 正解：情况 ：该等腰三角形的底角度数为 ；情况 ：该等腰三角形的顶角为 ，底角为 .

归纳模型

已知等腰三角形一角度数为 ，求该等腰三角形的底角度数^[2]. （图1）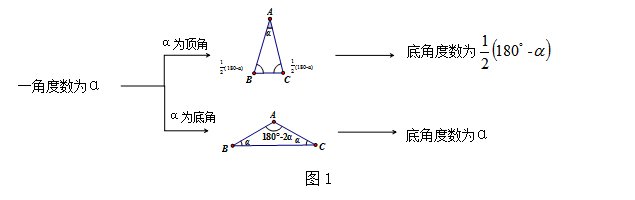

例4：等腰三角形一腰上的高与另一腰的夹角为 ，求该等腰三角形的底角度数.

解：按三角形角的分类，可将此等腰三角形分为锐角、直角、钝角等腰三角形三种情况进行讨论。

情况 ：该等腰三角形为锐角等腰三角形. 如图2，∵在 中， ， ，∴ ，∴ .

情况 ：该等腰三角形为直角等腰三角形，不满足题意，故舍去.

情况 ：该等腰三角形为钝角等腰三角形. 如图3，∵在 中， ， ，∴ （三角形外角定理），∴ .

综上所述：该等腰三角形的底角度数为 或 .

例5：等腰三角形一腰上的垂直平分线与另一腰的夹角为 ，求该等腰三角形的底角度数. (类比上述方法)

易错点：（1）对于此类只给文字而未给图形的几何问题，学生所熟悉的三角形一般均为锐角等腰三角形，所以惯性思维地只考虑了情况 ，考虑问题不全面. （2）对于那些不善于将文字语言转化为图形语言的学生，可能会出现画错图形，甚至画不出图形的情况，导致解题失败.

例6：在等腰三角形 中，设 ，当 有三个不同的度数时，请你探索 的取值范围. 分析：根据题意，可将 分为锐角、直角、钝角三种情况进行讨论.

情况 ：当 为锐角时，即 ，在等腰三角形 中，若 为顶角，则 必定为底角，∴ . 若 为底角，则① 为顶角， . ② 为底角， . ∵题目要求 有三个不同的度数，∴还需要满足 ，解得

情况 ：当 为直角时，即 ，在等腰三角形 中， 只能为顶角，∴ 只能为底角，不符合题意，故舍去.

情况 ：当 为钝角时，即 ，在等腰三角形 中， 只能为顶角，∴ 只能为底角，不符合题意，故舍去.

综上所述，当 有三个不同的度数时， 的取值范围为 且 .

归纳模型

问题是数学的心脏，数学问题的解决过程，实质是命题的不断变换和数学思想方法的反复运用过程. 因此，教师在解题教学时，不仅要注重学生对基础知识与基本技能的掌握情况，还应该重视对数学思想方法的渗透. 教师应该引导学生在理解题意、尝试解决、知识运用、解题反思各个环节中感受蕴含其中的数学思想方法，从而达到“授之以鱼”与“授之以渔”的双重期望.

参考文献

[1]方建文.对分类讨论思想的思考——以“等腰三角形中的问题”为例[J].数学教学通讯,2016(11):14-16.

[2]卢浩挺.基于分类讨论思想的等腰三角形复习[J].基础教育论坛,2020(16):8-11.

3