独立分量分析在脑电信号混合噪声分离中的应用

独立分量分析在脑电信号混合噪声分离中 的应用

薛松，耿晓中 *（通讯作者），陈杨

长春工程学院 计算机技术与工程学院， 长春  130012

摘要：在脑电信号的采集和处理过程中，常常受到各种噪声伪迹的干扰。本文将独立分量分析（Independent Component Analysis，ICA）技术应用在脑电信号的眼电噪声分离问题上。本文分别使用四种常用的ICA算法：二阶盲识别(SOBI)、Hyvarinen不动点算法(FastICA)、Infomax和联合逼近特征矩阵对角化(JADE)用于脑电信号的眼电伪迹分离，并使用MATLAB作为实验平台，采用格茨数据集2a，针对四种算法的运行时间及分配内存进行了实验对比。实验结果表明，SOBI算法的MATLAB实现表现了最好的综合性能。相较其他三个ICA算法，SOBI算法能够在分配内存较小的情况下快速准确地去除脑电信号中的噪声。

关键词：独立分量分析（ICA）；脑电信号（EEG）；盲源分离(BSS)；

1.引言

脑电信号（ElectroEncephaloGrapgy,EEG）是一类反映大脑活动的微弱生物电信号，其中包含了大量的生理和病理信息，在研究人脑功能、疾病预防及诊断等方面，EEG信号发挥了非常重要的作用。但是在脑电信号的采集过程中，经常受到诸如眼电、肌电、心电等外界的干扰，使得采集到的脑电信号中包含了严重的噪声伪迹，影响了脑电信号的分析及分类识别。因此，如何在确保不丢失脑电信号的前提下消除噪声伪迹，是脑电信号预处理阶段的一个首要研究内容。

盲源分离（Blind Sourse Separation，BSS）是盲信号处理领域中的一个主要研究方向，盲源分离算法能从观测到的混合信号中，提出未知的“源”信号。多导联采集到的EEG信号是由多个脑电“源”信号经由头部的容积传导效应混合形成的，因此，利用盲源分离的脑电信号分析方法能够有效地基于头皮空间域进行脑电信号分析。国内外学者提出了许多盲信源分离方法，其中基于统计独立性的独立分量分析（Independent Component Analysis，ICA）方法应用最为广泛。

ICA是一种多通道信号处理和数据分析方法，它能对由统计独立的“源”信号混叠而成的多路观测信号进行分离，还原出原始的多个独立“源”信号。传统的脑电噪声分析方法是直接从测量信号中去掉伪迹特征显著的记录。但是，这种方法容易导致大量脑电数据的丢失，尤其是在眼动期间大脑活动的数据，最终影响分析结果。由于脑电信号及眼动噪声是由相互独立的不同信号源产生，因此借助ICA技术能够有效分离出混杂在EEG数据中的眼动伪迹。

2．独立分量分析

2.1 ICA数学模型

已知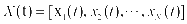 是一组N维观测信号，它是由一组M维相互统计独立的源信号 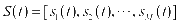混合而成，且S中至多包含一个高斯信号。则存在 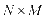维非奇异混合系数矩阵A使得：

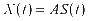（1）

由于源信号S及混合矩阵A均为未知，因此只能借助混合信号X及解混矩阵W提取出估计的源信号U，分离过程可表示为：

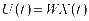（2）

其中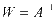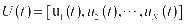， ， ICA的目标是寻找解混矩阵W，使得能够仅通过N维混合信号X分离出独立的估计信号U，U最佳逼近于源信号S。

当前，较常见的ICA算法有：FastICA算法、infomax算法、SOBI算法及JADE算法，以下分别介绍这几种算法，并通过实验进行性能的对比分析。

2.2 FastICA算法

FastICA算法是一种基于快速寻优的定点迭代算法。对于负熵最大的FastICA算法，把随机变量的负熵做如下定义：

(3)

其中，x_g是一个高斯随机变量，它与随机变量x具有相同方差。H代表随机变量的微分熵。由于缺乏源信号的先验知识且随机变量的概率密度分布函数未知，因此常利用以下近似公式（4）表示负熵：

(4)

式（4）中，E[ ]是均值运算，G（）是非线性二次函数。

FastICA算法的核心是通过选取合适的分离矩阵W，使得负熵J(W^Tx)的值最大。在均值等于0且方差等于1时，求解J(W^Tx)的最大值可以等价为求E[G(W^Tx)]的最大值。利用牛顿迭代法进行计算与化简，得到近似的FastICA迭代公式：

(5)

式（6）中， 是 的一阶导数; 是 的二阶的导数。

通过多次迭代求得分离矩阵W，最终将混合信号X分解为多个独立成分的集合U。

2.3 Informax算法

Informax算法的主要原理是通过引用一个非线性函数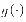 ，致使新向量Z=g(U)的熵极大化，进一步等价于U中各分量独立性的最大化，构成U中的各分量独立性判据。依照这一判据，Informax算法调节W，最终使U中各分量独立，最终实现了ICA分解。扩展Informax算法中的解混矩阵调节公式表示如下：

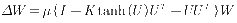(6)

式（6）中： 代表单位矩阵； 代表对角矩阵。

扩展Informax算法的主要步骤如下：

1. 对源信号实施去均值和白化处理；

2. 对分离矩阵W初始化；

3. 计算U和 ；

4. 调整 ；

5. 重复步骤（3）和（4），直到 收敛；

6. 得到独立分量 。

2.4 SOBI算法

SOBI算法通过对一批方差矩阵实施联合近似对角化达到信号盲源分离的目标。SOBI算法进行盲源分离的主要步骤如下：

1. 对观测信号 (t)进行白化处理；

2. 计算采样协方差矩阵 ；

(7)

式（7）中，R_s是源信号S的相关矩阵，R_x为滞后相关矩阵。

3. 计算正交矩阵Y；对于全部 使用联合近似对角化算法，得到正交矩阵Y，其满足下式。

(8)

其中， 是一组对角矩阵。

4. 计算混合源信号矩阵 ；由上述可以求出：

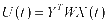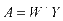， (9)

式中： 为重构后的观测信号， 为分离矩阵 的伪逆矩阵。

2.5 JADE算法

JADE算法假设有用的信号是非高斯分布，而噪声信号是高斯分布。设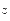 为球化后的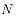 通道观察矢量 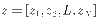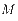， 为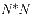 矩阵。则JADE步骤如下：

1. 求球化阵 ，令 ；

2. 对于 ，根据球化数据 定义球的一组 ， 。其中 ， （10）

3. 通过优化步骤求出 ，使得所有 联合对角化。

4. ICA辨识的分离结果表示为：

（11）

3.ICA分离脑电信号噪声实验

3.1数据描述

本次实验使用第四届国际脑机接口竞赛——格茨数据集2a（BCI计算机IV-数据集2a）.。

受试者舒适地坐在电脑屏幕前的扶手椅上。在实验开始时（t=0s），黑屏上出现了注视叉，此外，还给出了简短的声音警告音。两秒钟后（t=2s），屏幕上出现了一个箭头形状的提示，分别指向左，右，上或下（对应于左手、右手、脚或舌头四类之一），在屏幕上停留连续1.25秒，受试者执行所提示的运动想象任务。直到在t=6s时注视十字从屏幕上消失为止。随后短暂休息，屏幕再次变黑，时间顺序如图1所示。本实验用22个Ag/AgCl电极记录EEG信号，其中有3个电极应用于EOG信号的采集。

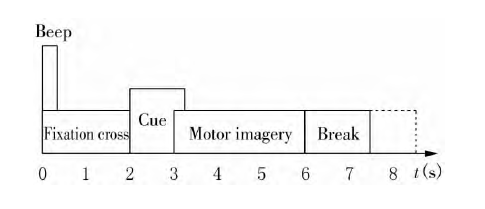
图1 实验时间安排

3.2脑电信号分离实验

本文使用MATLAB作为实验平台，使用第一位受试者的测试数据集。为了减少眼电伪迹的干扰，本次实验选取了1~22电极通道的脑电数据。本实验也对数据集进行了特定区间提取，仅提取了实验开始处1~3s的脑电数据，因为这段时间不但可以表示整个运动想象的过程，而且降低了脑电数据处理的复杂度。观测信号的脑电波形如图2所示。

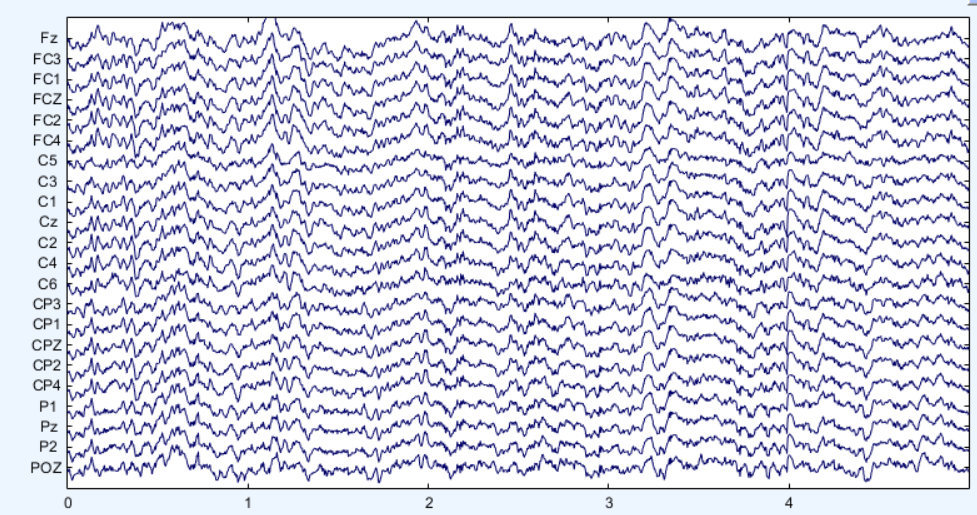
图2 观测信号

在ICA分析中，眼电伪迹的识别是一个重要步骤。重构EEG信号首先需要能准确地识别出EEG信号中混杂的眼电成分，然后才能去除眼电独立成分。本实验分别采用Fast ICA算法、SOBI算法、Informax算法及JADE算法实施独立分量分解，去除眼电伪迹后得到重构的EEG信号，如图3、4、5、6所示。因为通道数是22个，所以对应的独立分量数也设置为22。可以明显看出，相比混有眼电伪迹的观测信号，由四种ICA算法得到的重构EEG信号都比较干净，去噪效果较好。

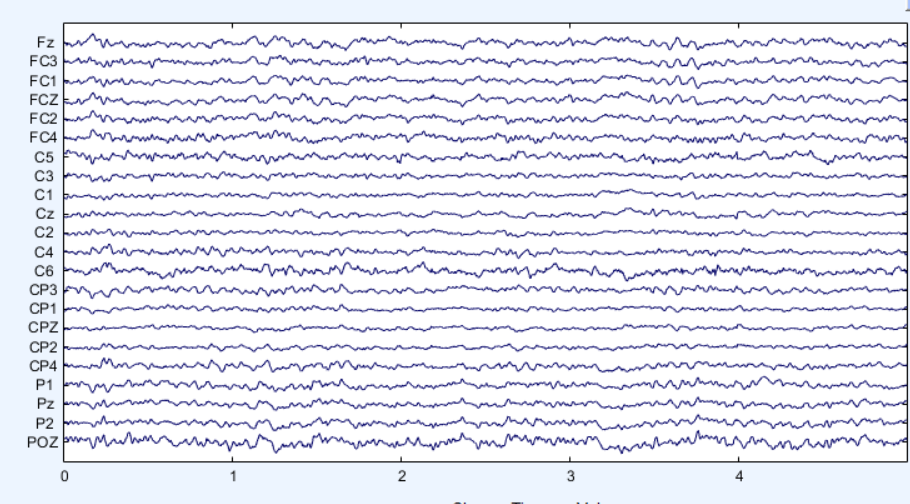
图3 FastICA方法得到的重构EEG信号

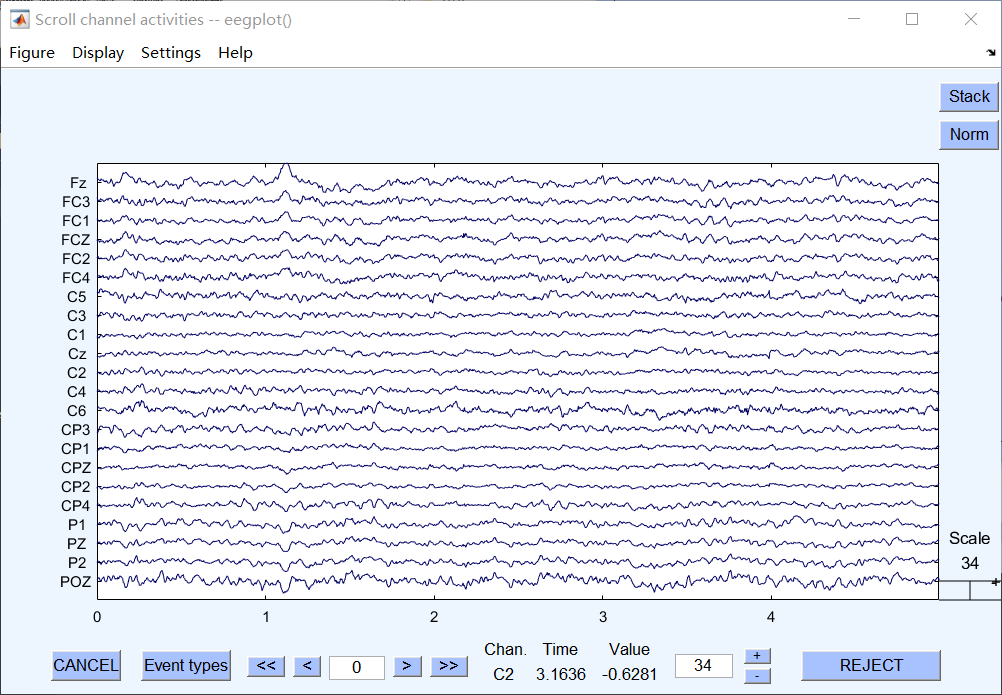
图4 SOBI算法得到的重构EEG信号

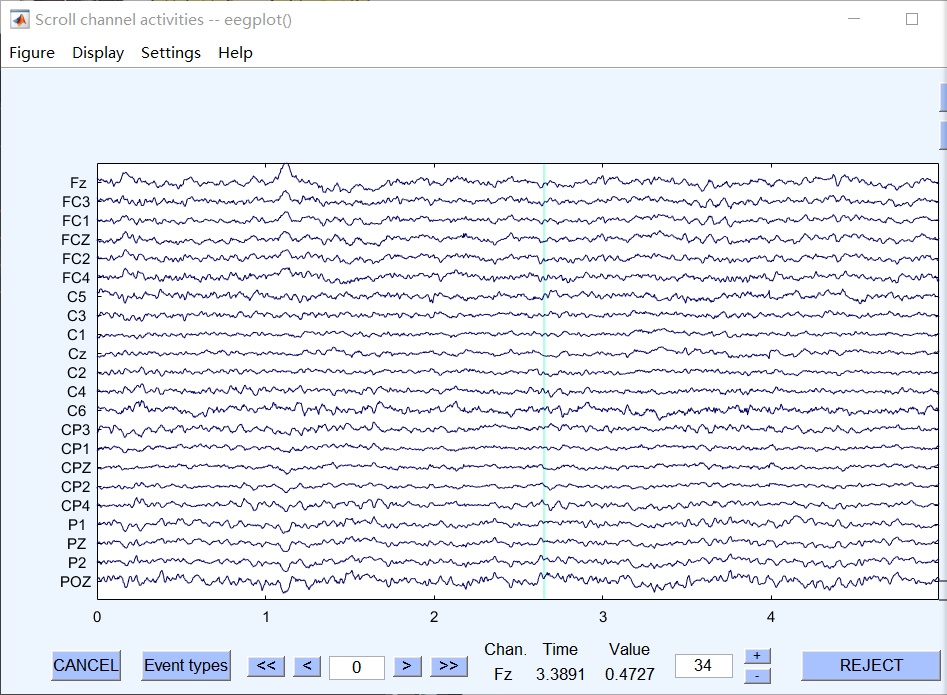
图5 Informax算法得到的重构EEG信号

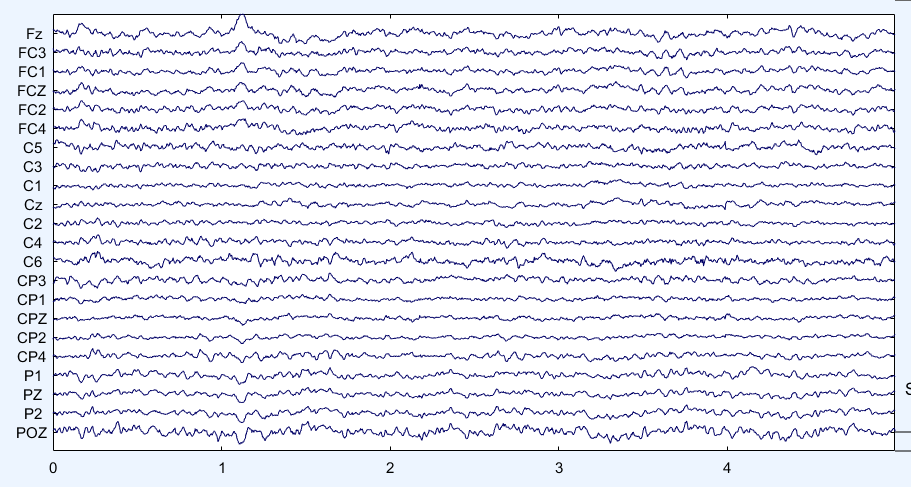
图6 JADE算法得到的重构EEG信号

3.3 四种算法性能的比较

本文实验中四种ICA算法使用的实验数据皆为第一位被试者的测试数据集，并针对每种算法进行了多次实验，用于实验的PC机的处理器频率为2.4GHz，处理器是Intel Core i7，内存16GB。对于运行时间和分配的内存测量，本文使用了内置的MATLAB函数。对于运行时间测试，使用了MATLAB函数tic-toc。另一方面，对于分配的内存测试，将为每种算法的每个运行实例创建一个配置文件。

四个算法的运行时间和分配内存对比图分别如图7和图8所示。

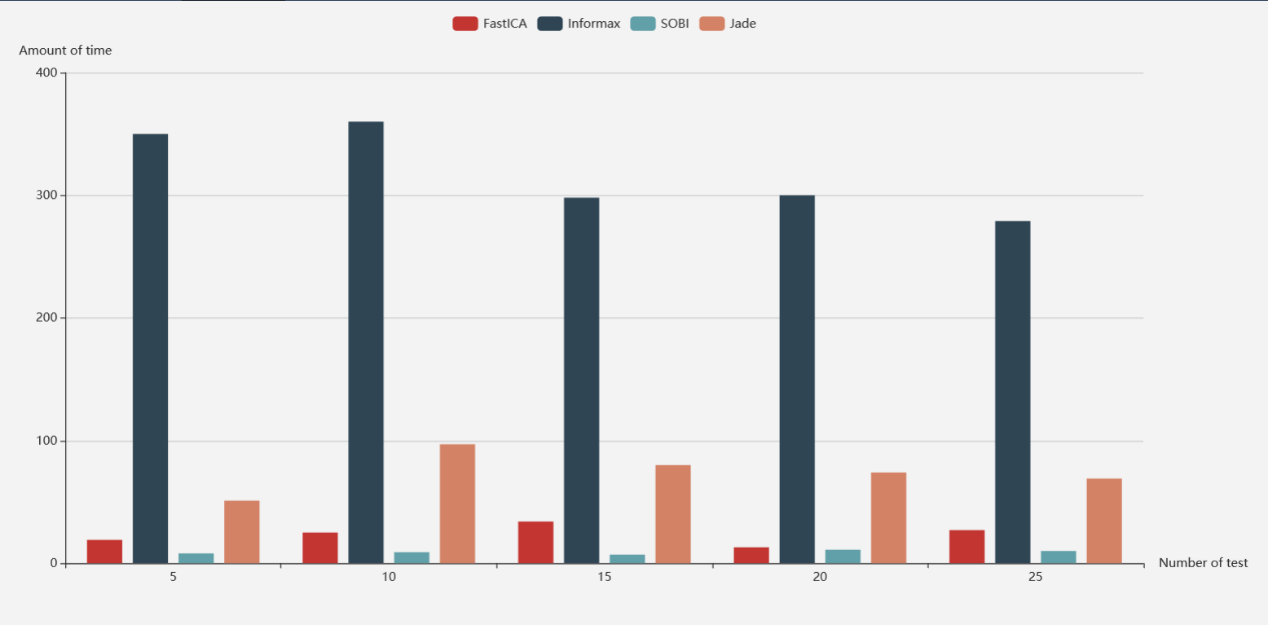
图7 ICA算法的运行时间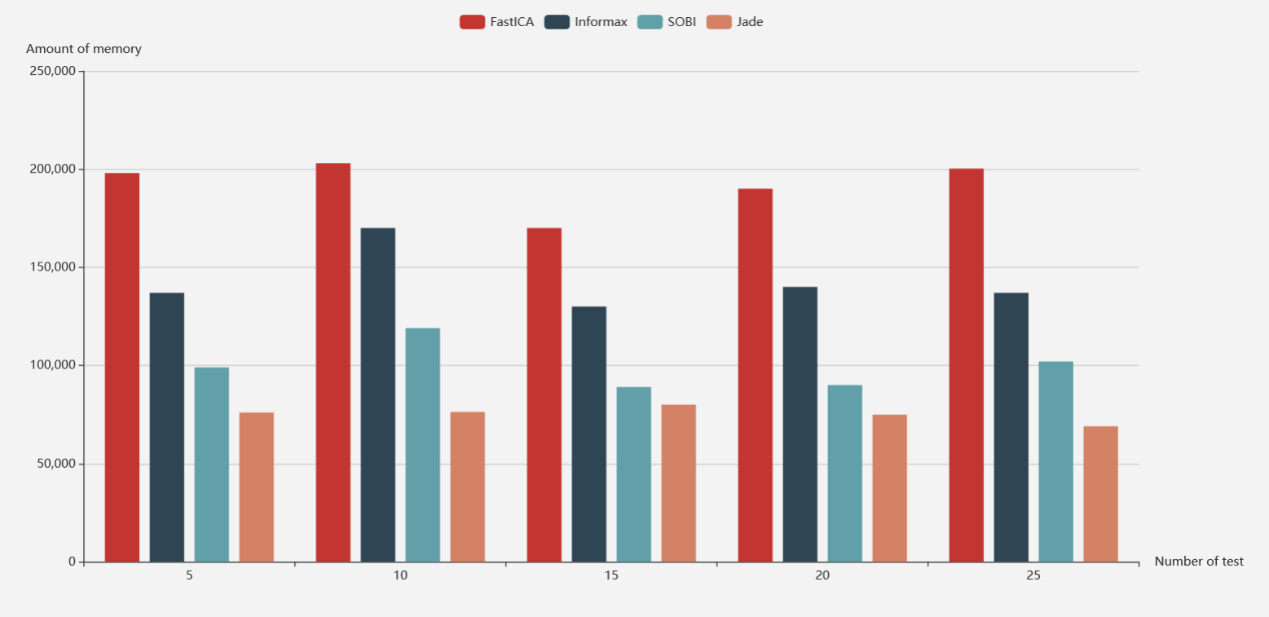

图8 ICA算法分配的内存

从图7中可以看出，对比其他三种算法，SOBI算法的运行时间最小，这是由于SOBI算法依据二阶统计量作出分解，计算较简单。尽管FastICA算法比SOBI算法略逊一筹，但也较快，这是由于FastICA算法使用了牛顿法的迭代过程，因此收敛有保证，而且该算法一次只提取一个独立分量，计算量较小，所以提取速度较快。Informax算法运行时间显著大于其他算法，这是因为其收敛速度较慢，所以数据需要较长时间才能够把各信号间的独立性展现出来。从图8中可以看出，FastICA总是需要分配比其他算法更多的内存，而JADE算法需要分配的内存最少。

综合图7、8可以看出，SOBI算法在使用适度内存的同时具有最少的运行时间。尽管FastICA算法是一种快速的算法，但是该算法使用的内存通常都高于其它三种算法。Informax算法的运行时间和分配的内存与其它算法相比都不具有优势，但是该算法具有一定的稳定性。JADE算法虽然在速度上有点慢，但是该算法分配的内存较少，可以考虑对JADE算法进行适当的并行化，使运行速度加快。

4.结论

本文研究分析了独立分量分析的四种不同算法：SOBI、FastICA、Infomax和JADE，并将这些算法应用于诱发电位信号的噪声分离实验中。实验表明四种ICA算法都能够较好地把源信号和噪声分离出来，有效地去除噪声对源信号的干扰，进而有效地提高分类识别的准确率，SOBI算法的表现了最好的综合性能。本文的ICA算法性能对比分析为ICA的研究提供了理论及实验基础。

参考文献：

[1] Guillermo SAHONERO-ALVAREZ, Humberto CALDERON. A Comparison of SOBI, FastICA, JADE and Infomax Algorithms. Proceedings of The 8th International Multi-Conference on Complexity, Informatics and Cybernetics (IMCIC 2017), 17-22

[2] 耿晓中，李得志. 基于独立分量分析的眼电伪迹去除方法研究[J]. 长春工程学院学报 （自然科学版）. 2020, 21(1)：78-81

[3] 邹凌，王新光，马正华. 基于独立分量分析提取仿真脑电诱发电位信号[J]. 中国组织工程研究和临床康复，2009，12(17)：2365-3267

[5] 王彬，高冰，古沛尚，辛凤鸣. 基于FastICA的低信噪比雷达信号分选算法[J]. 东北大学学报，2019，11

[6] 赵岩岩. 基于运动想象的脑电信号特征提取及分类算法的研究[D]. 哈尔滨:哈尔滨工程大学.2016

[7] 郭文强，潘丽，赵文卓，邱天爽.基于参考信号的ICA方法进行诱发电位单导提取[J]. 生物医学工程学进展，2008，1

（202111437029，大学生创新创业训练计划项目）