基于堆叠式LSTM的剩余寿命预测研究Research of a remaining useful life prediction method based on stacked LSTM

基于堆叠式LSTM的剩余寿命预测研究Research of a remaining useful life prediction method based on stacked LSTM

汪辉

海节卡机器人科技有限公司

摘要

目前，常用寿命预测方法在处理多变量输入数据时，与实际寿命存在较大偏差。鉴于此，本文提出一种基于堆叠式LSTM (Long Short-Term Memory) 的寿命预测方法。该方法通过架构双层LSTM模型，以增加模型的深度。同时，添加Dropout层，来提高模型的泛化能力。最后展开寿命预测实验。相比传统单层LSTM算法，本文方法可降低误差达23%。相比堆叠式RNN算法，可降低误差达47.86%。实验结果表明，本文方法预测精度高、泛化能力强、收敛速度快。具有良好的工程应用价值及通用性。

关键词：堆叠式LSTM、记忆块、泛化能力、预测方法、RUL

Abstract

The traditional RUL (Remaining Useful Life) prediction methods exists a large deviation from actual values Due to mass of data input. A method based on stacked LSTM (Long Short-Term Memory) is proposed, which utilitzes two-layer LSTM to increase model depth. Meanwhile, a dropout layer is added to improve the model generalization. The experiment is carried out, and the MAE (Mean Absolute Error) of this method can be reduced by 23% and 47.86% respectively compared with the single-layer LSTM and the stacked RNN methods. The results show that the proposed method has high prediction accuracy, strong generalization, and fast convergence, which has great potential for applications.

Keywords：Stacked LSTM、Memory Unit、Generalization、Prediction method、RUL

引言

发动机是一种把其它形式的能转化为机械能的机器。它是设备运行的核心。如果发动机出现故障，将会造成安全隐患，导致经济损失。因此建立行之有效的发动机健康程度监测和RUL（Remaining Useful Life 剩余使用寿命）预测，具有相当重要的现实意义[1]。

当前，寿命预测方法主要分为机理模型、概率统计、神经网络与深度学习三类。机理模型法是根据物理现象，分析设备失效原理，建立精确的数学模型。比如累积损伤理论、断裂力学理论、裂纹扩展理论等[2]。这类方法物理意义明确。可是一旦设备结构复杂，耦合因素较多时，则难以建立准确的物理模型；概率统计是根据先验知识，采用统计手段，来预测设备发生故障的概率。如贝叶斯决策、最大熵模型、支持向量机等[3]。在实际应用中，Lv等人[4]通过粒子群算法来优化向量机参数，来提高模型的收敛速度。Wang[5]等提出基于多核相关向量机的轴承寿命预测法，来解决先验知识较少时向量机核函数难以选择的问题。以上概率统计法多用于处理小样本数据，不适合大量数据，会存在耗时较多、模型不收敛的问题；神经网络与深度学习方法是通过实时采集设备的运行时间、振动频率、内部温度等信息，并建立网络模型，最终建立参数和剩余使用年限映射关系。如BP网络、随机森林、强化学习等[6]。在实际应用中，刘桓龙等人[7]利用BP神经网络构建轴承的RUL预测模型。Gebraeel等人[8]采用前馈神经网络搭建预测模型。Wu等人[9]提出基于ANN（Artificial Neural Network，ANN）网络的预测模型。李婉华等人利用随机森林算法对用电负荷进行预测[10]。可是，以上网络未考虑时间维度。对于RUL预测来说，时间维度是必须考虑的因素。因为RUL需要根据设备的退化趋势，预测设备未来的退化程度。鉴于此，循环神经网络RNN（Recurrent Neural Network）被引入。它通过对含有时间信息的数据进行迭代学习，实现预测。但是，若RNN网络存在小权重参数时，这些参数可能在数次迭代相乘后，梯度值减小到零，导致梯度消失。鉴于此，LSTM算法对RNN进行了改进，它将参数相乘改为参数相加，避免了此类现象

[11]。目前LSTM算法已应用在电力负荷预测[12]、交通预测[13]及水文预测[14]等领域。这些领域因为输入参数较少，所以简单的LSTM模型尚能满足预测要求。但是像航天航空领域，输入数据多达几十种。而且数据间还存在非线性、强耦合、多模态的特性[15]。若再采用传统LSTM模型，则难以映射这么多参数，从而造成预测精度下降，亟需解决。

本文给出一种堆叠式LSTM算法。通过增加网络深度、记忆块数量、Dropout层的方法来提高预测精度。为航天领域的发动机寿命预测提供新思路，文章结构为：首先介绍堆叠式LSTM算法原理，接着处理数据、搭建模型，最后开展实验、进行分析。

1堆叠式LSTM算法原理

图1(b)是LSTM单元---“记忆块”，包括输入门、遗忘门、输出门。通过这些门的开闭，可以让一些数据有选择的通过、去除、和增加[16]。因此LSTM模型在自循环运算时，可自主改变权重和积分尺度，避免梯度消失或者梯度膨胀现象。图中红色箭头线是LSTM是信息传递的关键线路，他可将当前时刻信息传输给下一时刻。通知这种方式，Yt不仅与当前状态t有关，还和之前状态t-1，t-2，……有关，实现LSTM对重要特征的记忆。

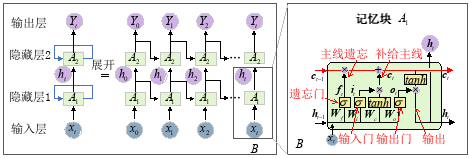
图1 双层LSTM结构与记忆块单元

(1)

公式1显示了LSTM单元工作流程：首先拼接xt和上一时刻隐向量ht-1，形成，为后续门控机制做准备。然后， 分别与四个权重Wf、Wi、Wc、Wo建立连接，并在自循环中更新权重。接着，通过sigmoid函数 (σ) 来开关“遗忘门”ft，以决定是否让上一时刻信息ct-1通过或部分通过。此外，sigmoid函数还决定“输入门”it的开关，以决定哪些值需要更新。接着用tanh函数生成新的候选值。并将上一时刻信息ct-1乘以ft，从而忘记不需要的信息，并与相加，得到ct。最后，通过sigmoid函数来得到一个初始输出ot，再使用tanh将ct值缩放到[-1,1]。并与输出门ot叉乘，得到模型输出ht。

图2堆叠式LSTM结构

上述为单个LSTM工作原理。如将两个LSTM上下叠加可形成双层LSTM (图1(a))，它包括输入层、隐藏层1、隐藏层2、输出层。在t时刻，输入的特征向量为xt、隐藏层输出为ht、输出结果为Yt。同理，将多个LSTM组合就可组成堆叠式LSTM。在图2中，第一层LSTM输出交给Dropout层。Dropout层会删除部分数据以防止过拟合。接着数据将传输给第二层。然后传输给第三层，最后数据进入Dense层，进行特征提取与非线性变化处理，最终输出预测结果。由于堆叠式LSTM可在高维更抽象的表达xt状态特征，因此可以显著低迭代次数、增加预测准确率。基于此方法，下一节将搭建发动机寿命预测模型。

2数据处理与模型搭建

这里给出100个航空发动机的全生命周期数据[17]。如图3所示，数据包括发动机ID号、运行时间cycle、操作设置set1、…、操作设置set3、传感器数据p1、… 、传感器数据p21共27个参数。这些数据被分为训练集train['ID'、'cycle'、'set1'、…、'set3'、'p1'、…、'p21'] 共20631行，测试集test['ID'、'cycle'、'set1'、…、'set3'、'p1'、…、'p21'] 共13096行。此外，真实集truth['ext']中有100个数据，其为每个发动机多余的RUL。计算流程如下：

图3 数据样式与数据处理

1)分别计算train集和test集对应的RUL，即train ['RUL']和test['RUL']。

在训练集中，找出同一ID对应的最大cycle值train['max']，用此值减去每行cycle值train ['cycle']。得到train ['RUL'] = train['max'] - train ['cycle']。

在测试集中，找出同一ID对应的最大cycle值test['max']，用此值减去每行cycle值test['cycle']，并加上truth [''ext''], 得到test['RUL'] = test['max'] + truthf[''ext'']- test['cycle']。

2)数据处理

除ID、cycle、RUL以外，对所有数据进行归一化处理，从而避免大数变化掩盖小数变化；如图3红框所示，依次以50行数据为一矩阵，作为每个ID号对应的输入X  (不考虑最后一行数据，共15631个矩阵)；从每个ID的第51行开始，依次读入train ['RUL']数据，作为输入数据Y，共15631行数据。

3)平台搭建

硬件平台为PC机，采用AMD Ryzen 7 3.2Ghz CPU、16G 3200MHz内存。软件平台为Visual Studio Code，并搭载keras人工神经网络库。模型采用双层LSTM (图1)，并用python语言编写。输入参数为X和Y。第一层的记忆块数量为100，第二层记忆块数量为5。Dropout层的舍弃率为10%。损失函数采用均方误差。最大迭代次数设置为100次，梯度更新的样本设置为32。

3实验与对比分析

1)实验分析

表1本文方法的关键指标

本次实验一次性输入100个发动机的数据，共计15631个。用来训练模型的参数。经过23次迭代后模型收敛，表1给出模型关键指标。其中MAE (平均绝对误差)和R2 (绝对系数)的公式为：

                                        (2)

公式中m代表数据个数，Yi为真实值、为预测值、为真实值的均值。MAE和R2越小，说明预测值越准确。图4给出每次迭代对应的MAE曲线。其中训练集的MAE从66.6591降到11.7095，测试集的MAE从58.8988降到 18.5981。由于发动机数较多，图5只给出ID号为1和2发动机寿命预测结果。其中蓝线为真实RUL，红线为预测RUL。由图表可知，本文预测预测结果较为平稳，接近真实RUL。

图4 模型MAE值的变化 (a) 训练集 (b) 测试集

图5 发动机寿命预测结果 (a) 发动机ID 1 (b) 发动机ID2

2）对比分析

此外，分别搭建单层LSTM和双层RNN模型，来与本文方法对比。以测试集每个ID的最后50行数据作为输入X，以每个ID最后一个RUL值作为输入Y。如果某个ID不足50行数据，则直接跳过。这样共得到93组数据。在相同的环境下进行实验。实验结束后，表2显示了每种模型关键指标。图6给出预测结果。根据图表，分析如下：

方法1：单层LSTM结构简单，所以迭代次数和耗时最少 (21次和406s)。但本次实验输入变量多达27个，而单层模型难以在高维度表示多变量数据。造成MAE为15.1356。预测效果一般。

方法2：堆叠式RNN是将上一状态和当前输入一起和参数矩阵做计算。这种算法会造成信息“遗忘”。即使采用堆叠结构，依然无法彻底解决。此次实验，迭代次数39次、MAE高达22.4563、耗时共计521s。预测效果最差。

本文方法：综合RNN和LSTM优点，有效解决“遗忘”和无法在高维表示的问题。本次实验，迭代次数仅为23次，MAE仅为11.7095。计算可知，本文方法对比方法1，可降低误差达23%。对比方法2，可降低误差达47.86%。由图6也可以看出，本文方法偏离实际值较小，整体预测结果平稳，波动性小。具有良好的预测效果。

本文方法计算时间为505s，略长于方法1。这是由于搭建双层LSTM模型必定比单层耗时。可是在实际应用中，模型只需搭建一次，就可以进行数据预测。所以增加的计算时间可以忽略不计。综上所述，本文提出方法在时间和精度上取得良好的平衡。

表2三种方法的关键指标

图6 预测效果对比

结论

本文提出一种基于堆叠式LSTM (Long Short-Term Memory) 的寿命预测方法。方法通过构建双层LSTM模型、采用门机制、添加Dropout层，来提高预测精度和泛化能力。实验表明。相比传统单层LSTM算法，本文方法可降低误差达23%。相比堆叠式RNN算法，降低误差达47.86%。本文方法预测精度高、泛化能力强、收敛速度快。具有良好的工程应用价值及通用性。

参考文献

[1]柳长源, 何先平, 于会越. 基于数据驱动的涡轮发动机剩余寿命预测[J]. 电机与控制学报, 2021, 25(7):7.

[2] Dong M, He D, Banerjee P, et al. Equipment health diagnosis and prognosis using hidden semi-Markov models[JJ. Int J Adv. Manuf Technol, 2006,30(7- 8):738-749.

[3]陈雄姿, 于劲松, 唐荻音,等. 基于贝叶斯LS-SVR的锂电池剩余寿命概率性预测[J]. 航空学报, 2013, 034(009):2219-2229.

[4]Lv X S. Application of support vector machine with particle swarm optimization algorithm in blasting vibration prediction[C]. ICEEE 2010 International Conference. 2010.

[5]Wang B, Lei Y, Li N, et al. An improved fusion prognostics method for remaining useful life prediction of bearings[C].International Conference on Prognostics and Health Management. IEEE,Singapore,2017:18-24.

[6]齐申武. 基于振动信号分析的滚动轴承故障诊断及寿命预测研究[D]. 燕山大学.

[7]宁武龙, 刘桓龙, 彭卫池,等. 基于BP神经网络的轴承寿命预测程序设计[J].现代机械, 2014(3):7-10.

[8]Gebraeel N,Lawley M,Liu R,et al．Residual life predictions from vibration －based degradation signals：a neural network approach [J]．IEEE Transactions on Industrial Electronics,2004,51(3):694－700.

[9]Wu S J, Gebraeel N, Lawley M A, et al． A Neural Network Integrated Decision Support System for Condition －Based Optimal Predictive Maintenance Policy [J]．IEEE Transactions on Systems, Man,and Cybernetics－Part A: Systems and Humans, 2007, 37(2):226－236.

[10]李婉华，陈宏，郭昆，等. 基于随机森林算法的用电负荷预测研究[J]. 计算机工程与应用，2016，52(23)：236—243.

[11]张晨阳, 韦增欣, 郜星军. 基于LSTM模型的数学机理分析实证研究[J]. 中国管理信息化, 2019, 22(15):5.

[12]吴海洋, 陈鹏, 郭波,等. 基于注意力机制和LSTM的电力通信设备状态预测[J]. 计算机与现代化, 2020(10):5.

[13]黄海超, 陈景雅, 孙睿. 基于VMD-LSTM轨道交通客流预测模型[J]. 华东交通大学学报, 2021, 38(1):5.

[14]陶思铭, 梁忠民, 陈在妮,等. 长短期记忆网络在中长期径流预报中的应用[J]. 武汉大学学报:工学版, 2021.

[15] Saxena A , Kai G , Simon D , et al. Damage propagation modeling for aircraft engine run-to-failure simulation[C].2008 International Conference on Prognostics and Health Management. IEEE, 2008.

[16]周志华. 《机器学习》[J]. 中国民商, 2016, 03 (No.21):93-93.

[17] A. Saxena and K. Goebel (2008). "Turbofan Engine Degradation Simulation Data Set",NASA Ames Prognostics Data Repository, NASA Ames, Moffett Field, CA.

作者简介：汪辉，男，博士，长期从事机器人感知与控制技术、机器人应用与开发、人机交互技术等方面的研究工作。

通讯作者：汪辉

单位：上海节卡机器人科技有限公司

通讯地址：上海市闵行区剑川路610号33-35号楼

邮编:200241

邮箱：hui.wang@jaka.com