小学数学“数与代数”的问题解决策略

小学数学“数与代数”的问题解决策略

吴桢萍

重庆市沙坪坝区新桥小学校，400000 

摘要：小学阶段的数学知识是学生学习数学的基础，而解决问题又是整个知识体系中最为重要的部分之一，传统的教学只是针对某个年级、某种题型进行讲解，将“问题解决”变成了“问题解答”，其实整个小学阶段的解决问题之间是有联系的，只有掌握了整个知识体系之间的联系，我们的学习才会变得融汇贯通。

关键词:数与代数；问题；联系；转化；策略

我国著名的教育家陶行知说过“创造始于问题，有了问题才会思考，有了思考，才有解决问题的方法，才有找到独立思路的可能。”因此掌握“问题解决”的策略和方法是培养学生能够用数学的思维去观察、发现和解决问题关键。

在整个小学阶段，“数与代数”中“问题”的类型包括：数的认识和运算、常见的量、式与方程、比与比例以及探索规律，其中探索规律贯穿在前面4种类型之中。下面，我就小学数学课堂教学“数与代数”中“问题”的类型及“解决”的策略进行阐述。

一、在“数的认识和运算”中培养学生的数感

英国数学教育家安吉莱瑞说过：孩子们具有“数感”的典型特征是他们对所遇到的数字模式和计算过程做出归纳，并能把新知识和已有知识相联系。“数的知识”贯穿在整个数学学习的历程中，培养数感可以让学生学会“数学的”思考，学会从现实情境中提出数学问题，学会将生活中的问题转化成数学问题，学会用数学的方法和数学的观点解决实际问题，从而构建与具体事物相联系的数学模型，好的数感是学生数学思维培养的重要前提。例如：在教学“0”的认识的时候，有些同学不理解为什么“0加任何数”和“任何数减0”都是这个数本身，那么我们就可以结合生活实际，充分唤醒学生的已有认知，让学生明白“0”表示没有，所以无论有多少加上没有或者减去没有就相当于原数没有发生变化因此得数还是原来的数，这样的思想在后面“0乘任何数”和“0除以任何不为0的数”时也可以从乘除法的本质涵义和0的本身的意义来理解，就会轻松理解为什么“0乘任何数”和“0除以任何不为0的数”都得0的结论。所以，把对数的认识以及对数的加、减、乘、除法的理解，应用于实际生活问题的解决中来，进一步体会生活和“数的认识与运算”之间的联系。

二、在“常见的量”中以“一”通“百”

在整个小学阶段，我们“常见的量”有质量单位、长度单位、时间单位、面积单位、体积单位等，这些“常见的量”之间的共同通点就是相邻两个单位之间有一定的进率，在转换的过程中方法都是：当将较大的单位转换成较小的单位时，单位前的数据要乘它们之间的进率；当将较小的单位转换成较大的单位时，单位前的数据要除以它们之间的进率。因此，只要我们牢记单位之间进率，理解单位之间的关系，结合生活的实际，在做题时有针对性的做出相应的转换，做此类题就变得轻松了。如甲瓶酒精重1.5千克，乙瓶酒精重1050克，哪一瓶酒精重一些？要比较哪一瓶酒精重首先我们要把单位进行统一才能比较，通常情况下，为保证转化后的数据是整数，我们一般将大单位转换成小单位，单位变小了，数据变大，已知1千克=1000克，通过转换我们知道1.5千克=1500克，因此甲瓶要重一些。

从最初的长度单位到后面的体积单位，单位转换的方法都是由长度单位转换的方法“迁移”应用的，这种“迁移”的思想不仅在解决“常见的量”问题中有所运用在整个小学阶段，“迁移”的思想贯穿于我们数学学习中的任何方面，如：计算、图形的认识等，我们要让学生学通、学懂这种思想方法，将方法内化然后学会将这种思想方法应用于数学学习的整个过程中。

三、在“式与方程”中将解决问题变得轻松

“方程”思想是“数与代数”中建模的重要体现，从大的方面来讲，它可以表达显示世界中的各种等量关系，从小的方面来讲，它是数学史上初等数学代数领域的重要内容。列方程是“数与代数”中解决问题的重要方式，是将具体数学问题转化为抽象数学模型的重要思维方式。运用字母将原本抽象、复杂的问题变得直观、简单，能便于我们的理解与接受。如最著名的“鸡兔同笼”问题：今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？如不列方程，常规的方法有假设、猜测、枚举等等，过程复杂，但如果设鸡有x只，则兔就是35-x，因为鸡有2足，兔有4足，于是列出方程2x+4（35-x）=96，算出鸡有22只，兔有13只。

“方程”的学习出现在小学5年级，是在学生已经完全具备整数、小数、分数的四则运算的能力和掌握在数学信息中寻找等量关系的方法的基础进行教学的。但让学生从以前的顺向思维一下转变成有未知数的逆向思维，对于小学生来说对未知数的使用还不是太习惯，究其原因，除了学生对新知识的接受还需要时间消化，其根本的原因是学生的“建模”思想还未形成，最具体的表现在对等量关系的建立能力不足。因此教学“问题解决”时，教会学生如何寻找等量关系是关键。

四、在“比与比例”问题中使巧劲

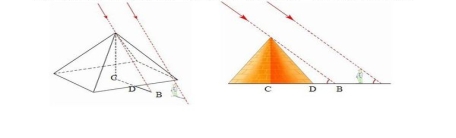
“比和比例”是传统算术的重要内容，既是老师教学的重点，也是学生学习的难点。其实在较早的年代，许多实际的问题都是通过“比和比例”的知识来解答的，许多看似无法解决的问题用比例法解决显得简单、方便、容易理解。例如在测量金字塔高度的时候，比例法就凸显了自己独特的魅力：金字塔是世界著名的建筑，尤其是胡夫金子塔尤为著名，金字塔建成后，国王提出一个问题，金字塔到底有多高呢？由于金字塔是锥形的且很高，直接测量很不现实，当大家都一筹莫展的时候，数学家塔里斯想出了办法，他想出在金字塔前竖立一根竿子，测出竿子的长度和竿子影子的长度，然后测出金字塔影子，竿子和竿子影子的比例就是金字塔和金字塔影子的比例，从而算出金子塔的高度。

“比和比例”的学习安排在小学六年级，是小学阶段“数与代数”的最后一个知识点，因此对“比和比例”的学习需要学生对之前知识点的牢固把握，同时需要结合生活实际来帮助学生理解。

小学数学是学生学习数学的起点和基础，而解决问题在小学数学中占有非常重要的位置，因此，理清小学数学中“数学问题”的题型及解决的方法是我们掌握如何解决问题的重要策略。

参考文献：

[1]章慧琴.小学数学“数与代数”课堂教学策略研究.[J]数学大世界旬刊，2017（6）

[2] 潘海艳.探究小学数学数与代数的高效课堂教学策略.[J]中国校外教育旬刊，2015（1）