1.中煤科工重庆设计研究院(集团)有限公司,重庆市400042;
2.西华大学 电气与电子信息学院,成都市 610039
摘要:直接转矩控制存在输出定子磁链和转矩脉动大以及开关频率不稳定等问题。针对该问题,提出了一种考虑延迟补偿的模型预测直接转矩控制方法。本文在三相异步电机数学模型基础上,建立异步电机离散时间预测模型,以转矩和定子磁链差值作为目标函数,通过在线评估开关矢量对电机的作用效果,选择最优目标函数,优化系统结构。并通过仿真模型验证了该算法的可行性与有效性。
关键词:异步电机;模型预测;延迟补偿
0引言
直接转矩控制(Direct Torque Control, DTC)自20世纪80年代提出以来,得到了逐步完善和发展,并成为具有代表性的高性能控制策略之一[1]。直接转矩控制因能实现高性能的动态响应而有广泛的应用,但其存在输出转矩脉动大和开关频率不稳定等问题[2]。近年来,模型预测控制(Model Predictive Control,MPC)作为新型预测控制方式在电力电子领域受到广泛关注[3]。模型预测控制是一种非线性预测控制策略,处理非线性约束的适应力强,利用给定的目标函数作为优化准则,让控制具有灵活性。文献[4]提出模型预测直接转矩控制(Model Predictive Direct Torque Control,MPDTC)技术,其原理简单,易于处理非线性约束条件,已被广泛应用于电机控制领域。但是MPDTC在控制过程中存在大量计算,系统存在延迟问题[5]。
本文利用MPDTC思想,提出一种考虑延迟补偿的MPDTC方法,有效降低转矩脉动。首先建立异步电机数学模型,用两步预测法,推算出定子转矩和磁链的预测值;最后通过目标函数选择电压矢量控制异步电机,从而确立考虑延迟补偿的MPDTC方法。
1逆变器驱动异步电机模型
图1所示是一个三相电压型逆变器驱动异步电机等效图。

图1 三相电压型逆变器驱动异步电机等效图
定义开关函数为:
![]() (1)
(1)
其中,x=a,b,c 。异步电机在两相静止坐标系下方程为
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
式中:![]() 、
、![]() 分别为定子和转子电阻;
分别为定子和转子电阻;![]() 、
、![]() 分别为定子和转子电流矢量;
分别为定子和转子电流矢量;![]() 、
、![]() 分别为定子和转子磁链矢量;
分别为定子和转子磁链矢量;![]() 、
、![]() 分别为定子自感和转子自感;
分别为定子自感和转子自感;![]() 为互感;
为互感;![]() 为转子角速度;
为转子角速度;![]() 为电机极对数。
为电机极对数。
2模型预测直接转矩控制系统
本文MPDTC系统如图2所示。

图2 MPDTC系统框图
控制回路由一个外部比例积分速度控制器和一个内部MPDTC控制器构成。转子角速度参考值![]() 和转子角速度
和转子角速度![]() 的偏差经过PI调节器得到转矩参考值
的偏差经过PI调节器得到转矩参考值![]() ,定子磁链参考值
,定子磁链参考值![]() 设定为额定值,磁链估算值
设定为额定值,磁链估算值![]() 、
、![]() 由定、转子磁链观测器计算获得,再通过预测器预测出磁链和转矩预测值
由定、转子磁链观测器计算获得,再通过预测器预测出磁链和转矩预测值![]() 、
、![]() ,最后选择最小化目标函数的电压矢量来控制异步电机。
,最后选择最小化目标函数的电压矢量来控制异步电机。
2.1延迟补偿
传统预测控制算法需要进行大量运算,因此控制系统存在时间延迟。本文通过将系统的k+1时刻的变量作为初值,对k+2时刻的变量进行预测来消除延迟的影响。具体方法为先对电流和磁链进行预测,然后基于k+1时刻的电流、磁链预测值来预测k+2时刻的状态变量。对此,将目标函数定义为:
![]() (7)
(7)
图3、图4和图5分别对比了系统理想情况、有延迟无补偿、有延迟有补偿情况下系统输出跟踪路径。其中,![]() 、
、![]() 、
、![]() 分别为定子磁链参考值、不确定值、最优值。
分别为定子磁链参考值、不确定值、最优值。

图3 理想情况下跟踪路径

图4 有延时无补偿情况下跟踪路径

图5 有延时有补偿情况下跟踪路径
由图3看出,不考虑计算延时,系统在![]() 时刻可以将计算所得到的值直接应用于
时刻可以将计算所得到的值直接应用于![]() 时刻。在图4中,因为计算延时,在
时刻。在图4中,因为计算延时,在![]() 时刻,矢量方向已经不是当前时刻的最优矢量。在图5中,在
时刻,矢量方向已经不是当前时刻的最优矢量。在图5中,在![]() 时刻开始计算
时刻开始计算![]() 时刻的最优开关矢量,则在
时刻的最优开关矢量,则在![]() 时刻,可以直接将选定的最优开关矢量应用在
时刻,可以直接将选定的最优开关矢量应用在![]() 时刻。
时刻。
3系统仿真分析
为验证上述预测控制算法的有效性,本文用搭建了MPDTC的系统模型。该模型系统的参数如表1所示。
表1 异步电机和控制系统参数
参数名称 | 参数值 |
| 1.2 |
| 1 |
| 170 |
| 175 |
| 175 |
| 0.062 |
| 1 |
| 50 |
| 520 |
| 2850 |
| 20 |
在采样时间![]() =
=![]() 时,不同工况的仿真结果如图6至图10所示。
时,不同工况的仿真结果如图6至图10所示。
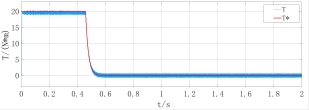


图6 空载起动转速升至150rad/s



图7 转速从15rad/s升至150rad/s
由图6可以看出,电机可以很好地跟踪给定转速,进入稳态后,定子电流脉动较小,波形比较平滑。
图7所示是电机半载起动。由图8可以看出,电机能够快速跟踪给定转速。
图8所示是当速度给定值为25rad/s时的转速图。
由图6、图7和图8可看出,电机在高速和低速,空
载和满载情况均运行良好,在全速度区内效果都比较理想,速度跟踪值可以快速、准确的收敛到真实值。系统具有良好的动态和稳态特性。
图9为带10N·m负载起动,转速给定150rad/s,1.5s时转速给定突变为-150rad/s。可以看出,电机正反转切换过程平稳。
图10为突加负载转矩时转速实际值和给定值,转矩、定子电流仿真结果。转速略有下降,但很快恢复至稳态,定子电流幅值稳定、脉动小。可以看出,MPDTC相对畸变率低,跟踪效果好。


图8 满载起动,转速为25rad/s



图9 半载起动转速从150rad/s变换至-150rad/s



图10 转速不变,转矩增大
4结论
本文研究了一种三相异步电机模型预测直接转矩控制方法,搭建了三相电压型逆变器驱动异步电机的仿真模型,并针对数字控制系统存在延迟问题,分析了一种带延迟补偿的MPDTC策略。通过改进目标函数以及转矩和定子磁链预测值,实现延迟补偿的模型预测控制。仿真结果表明,该方法的模型预测直接转矩控制异步电机系统运行中具有良好的静态、动态控制性能,具有一定的实用性。
参考文献:
[1]Casadei D, Profumo F, Serra G, et al. FOC and DTC: two viable schemes for induction motors torque control[J]. Converter Technology & Electric Traction, 2002,17(5):779-787.
[2]朱晓雨, 王丹, 彭周华, 等. 异步电机模型预测直接转矩控制[J]. 电机与控制应用, 2016,43(02):6-12.
[3]廖永衡, 冯晓云, 王珍. 基于定子磁链滑模观测器的异步电机空间矢量调制直接转矩控制[J]. 中国电机工程学报, 2012,32(18):88-97.
[4]Rodriguez J, Kennel R M, Espinoza J R, et al. High-Performance Control Strategies for Electrical Drives: An Experimental Assessment[J]. IEEE Transactions on Industrial Electronics, 2012,59; 59(2; 2):812-820.
[5]张永昌, 杨海涛. 异步电机无速度传感器模型预测控制[J]. 中国电机工程学报,2014,34(15):2422-2429.