水工码头桩基对上部建筑地震计算影响分析

水工码头桩基对上部建筑地震计算影响分析

周香琴

中交第三航务工程勘察设计院有限公司  上海 200030

摘要：对建于水工码头上的小型建筑物进行地震分析时，常将水工结构作为上部建筑结构的嵌固端，而仅对上部结构进行单独分析。本文应用多自由度体系的弹性地震反应理论分析水工码头的桩基刚度对上部结构地震响应的影响。通过对上部两层框架结构的模型计算，根据不同桩径、不同桩长情况下上部结构的地震分析结果，得出高桩梁板码头之上小型建筑物可单独计算的相应匹配条件。

关键词：多自由度体系；桩径；桩长；侧向刚度

1.研究背景

目前国内建于水工结构上的小型建筑物，在进行结构分析设计时一般将上部建筑结构单独隔离，认为建筑物嵌固在水工结构面上。

本文着重分析高桩梁板式码头对小型建筑的地震影响。一般码头上建筑物大多为工业用房，规模较小，本文为研究其所受地震影响，选取较简单的模型进行理论分析和数值分析。本文采用一栋两层两跨框架作为分析模型，用多质点弹性体系进行理论分析，数值分析采用MADIS GEN进行模态及内力分析。根据不同桩长、不同直径的桩基水工码头的计算实例分析，得出水工码头侧向刚度对上部建筑地震影响的相关规律及结论，对相应水工码头建筑的设计提出参考意见。

2.多自由度体系的弹性地震反应分析

上部结构选取两层框架，将水工码头视为一个质点，上部结构视为两个质点，根据弹性多自由度体系理论，用振型分解反应谱法来进行多自由度体系的地震反应理论分析。

（1）基本原理[1-3]

多质点弹性体系计算模型[1]如图1所示, 体系的运动方程为

(1)

根据振型正交性和振型叠加原理, 对振型进行分解，代入(1)式, 得到体系t 时刻第j 振型i 质点的水平地震作用为

图1 多质点弹性体系计算模型

(t)+(2)

体系j 振型i 质点水平地震作用标准值为(2)式的最大值

= = [+=(3)(i =1 ,…, n , j =1 ,…, n)

式中--相应于j振型自振周期的地震影响系数；--j振型i质点的水平相对位移；--j振型的振型参与系数。

对应于本文所取的两层框架模型而言，两层框架简化为两个质点，水工码头视为一个质点，第一个振型的参与系数

=

水平地震作用

(i =1 , 2 , …, n)

从上述公式可以看出，质点的质量与刚度对该质点受到的地震影响非常大。当桩长增长，导致层刚度减小，结构自振周期增大，底层位移增大，而二层以上各层位移会相应减小，高阶振型参与系数减小，相对于底层其余层振型参与系数都减小。当底层刚度远小于上部结构层间刚度，结构的水平位移主要集中于底层的水平变位，而上部结构近似于一个质点做整体平动，高阶振型相对于主振型影响很小。二层以上层间位移逐渐减小而底层层间位移逐渐增大，反应出底层水平地震作用逐渐增大，而二层以上各层水平地震作用力逐渐减小[4]。由此可见，对于水工码头桩长较长，刚度远小于上部结构的情况，整体计算时上部结构地震作用较小，因而在设计过程中不考虑水工码头影响，可直接单算上部结构。当桩长较短，刚度远大于上层时，底层与二层刚性联结，作为一个质点，则底层水平地震作用为零，而其余层水平地震作用增大[2]。该情况下单独验算上部结构，则会导致地震作用计算偏小，影响非常明显。

下文通过计算实例的数值分析，对上述理论分析结论进行验证。

3.数值分析

3.1 具体计算实例

本文利用有限元软件MIDAS GEN 对两层两跨钢筋混凝土框架结构进行计算，层高分别为5m，4m，设防烈度为7度，设计基本地震加速度0.1g，设计地震分组第一组，IV类场地。混凝土强度等级设为C30，钢筋采用三级钢（HRB400）。该栋建筑位于水工码头之上，水工码头根据实际情况选取了5榀排架，上部建筑位于中间区域。研究时根据水工码头的桩长特点，分别选取桩长10米、15米、20米、30米以及37米几种桩长类型。为了研究水工结构侧向刚度对上部建筑结构影响的规律，选取了不同桩径下的模型，包括0.6m 、0.8m 、1.2m 以及1.5m几种桩径进行分析。

3.2 计算结果分析

对选取的框架结构进行计算，结合结构的基本周期、层间刚度的变化，分别对不同情况下的结构计算结果进行了分析，主要分析对象是上部结构同一部位在地震作用下的内力，部位选取详见只有上部结构模型单元内力图中标示。由，增加质量m或减小层间刚度k，周期将增大，反之，减小质量m或增大层间刚度周期将减小。

上部结构模型单元内力图如下所示。

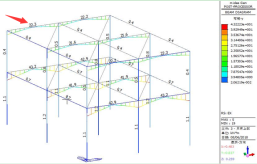
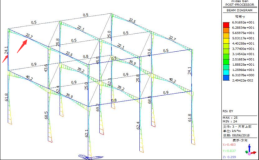
图2 EX工况下单元内力图  图3 EY工况下单元内力图

带水工码头时模型单元内力图桩径1.5米桩长5米时如图4及图5所示。桩径1.0米桩长15米时内力图如图6及图7所示。其余不同桩径桩长下相同部位的内力提取成表，见表1至表5。

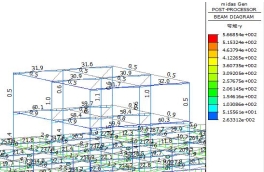
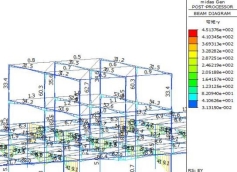
图4  EX工况下单元内力图一       图5  EY工况下单元内力图一

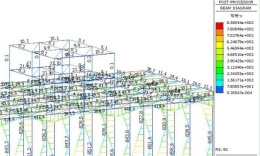
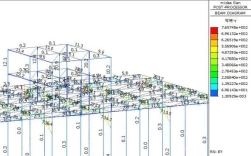
图6  EX工况下单元内力图二       图7  EY工况下单元内力图二

表1 桩径0.6米单元内力表

与不带水工码头的模型相比，根据5米桩长与10米以及15米桩长的结果，可以得出当底层刚度与上层刚度比在5米桩长时最大，约4.44倍，此时上部结构的地震工况下的内力小于单独计算上部结构模型。对比其他桩长结果，可发现内力均小于单独计算上部结果。因此当水工码头桩径小于等于0.6m时，可单独计算上部结构。

表2 桩径0.8米单元内力表

经过对比这个系列模型可知，当桩径为0.8m时，桩长5米时上部地震响应放大，底层刚度与上层刚度比约13.714倍。桩长10米时，侧向刚度比约1.79，,地震响应减弱。实际工程中，桩径0.8米时，一般桩长大约在10米以上，由此可见，在这种情况下也可不考虑带水工码头计算。

表3 桩径1.0米单元内力表

当桩径为1.0m时，桩长5米时上部地震响应放大，底层刚度与上层刚度比约32.448倍。桩长10米时，侧向刚度比约4.323，地震响应减弱。实际工程中，桩径1.0米时，一般桩长大约在15米以上，由此可见，在这种情况下也可不考虑带水工码头计算。

表4 桩径1.2米单元内力表

当桩径为1.2m时，桩长5米时上部地震响应放大，底层刚度与上层刚度比约64.462倍。桩长10米时，侧向刚度比约8.809，地震响应放大。桩长15米时，侧向刚度比约2.691，地震响应减弱。实际工程中，桩径1.2米时，一般桩长大约在15米以上，由此可见，在这种情况下也可不考虑带水工码头计算。

表5 桩径1.5米单元内力对比

通过上述几组模型的计算，认为水工码头的刚度并不能与地面相比，水工码头对地震的反应并不能像土对地震响应一样。不能简单地将建筑结构的模型简化为嵌固在水工码头面上，单独计算上部模型。在某些情况下，需要进行整体复核验算。

3.3 计算结果总结

总结以上系列模型，提取相同部位在地震工况下的内力，根据桩长、桩径的不同（即侧向刚度的变化）制出如下图表，用以表明地震内力的变化。

表6 底层与上层侧向刚度比值统计表

根据常用桩长桩径信息，通过系列模型结果对比，可以得到如下结论：

（1）桩径0.6米时，桩长一般为10米，通过数值计算可以发现此时底层水工结构层与上层侧向刚度比值较小，X向刚度比值小于1，仅为0.569，而通过其他模型也可以发现在0.6桩径的模型里，不管桩长是5米还是10米或15米，上部结构选取同一部位的地震工况下的内力均小于单独计算上部模型，由此可以认为这种情况下可直接计算上部结构，无需考虑水工结构的影响。

（2）桩径0.8米时，桩长一般为10米。可以看出10米桩长时，底层与上层X向侧向刚度比值为1.790，此时同一部位的内力仅为单独计算模型内力的0.54倍左右。当桩长为5米时，底层与上层X向侧向刚度比值为13.714，此时同一部位的内力为单独计算模型内力的1.52倍左右。桩长为15米时，内力比值仅为0.3左右。由此可看出在桩径0.8米，桩长为10米以上时，参考本文选取的上部结构参数，可单独计算上部模型。

（3

）桩径1.0米时，桩长一般为15米。15米桩长时，底层与上层X向侧向刚度比值为1.308，此时同一部位的内力仅为单独计算模型内力的0.45倍左右。而当桩长为5米时，底层与上层X向侧向刚度比值为32.448，此时同一部位的内力为单独计算模型内力的3.72倍左右。综合来看桩径1.0米，桩长为15米以上时，参考本文选取的上部结构参数，可单独计算。

（4）桩径1.2米时，桩长一般为15~25米。15米桩长时，底层与上层X向侧向刚度比值为2.691，此时同一部位的内力仅为单独计算模型内力的0.65倍左右。而当桩长为5米时，底层与上层X向侧向刚度比值为64.462，此时同一部位的内力为单独计算模型内力的2.327倍左右。根据变化规律可以推测桩长为15米以上时，上部内力均小于单独计算结果。综合来看桩径1.0米，桩长为15~25米时，参考本文选取的上部结构参数，可单独计算。

（5）桩径1.5米时，桩长一般为25~35米。通过系列模型可以看出当桩长小于15米时，底层与上层X向侧向刚度比值大于6，此时同一部位的内力均大于单独计算模型内力。而当桩长大于15米时，底层与上层X向侧向刚度比值小于6，此时同一部位的内力小于单独计算模型内力。综合来看桩径1.5米，桩长为25~35米时，参考本文选取的上部结构参数，可单独计算。

4.结论

水工码头对上部结构的地震作用影响与桩基刚度的大小是呈曲线变化的。根据数值模拟结果分析得出，当水工码头与上层结构的层刚度比值大于5且小于145时，底层水工码头对上部地震影响较大，计算时需要建立上部结构与水工码头的整体模型进行复核。当水工结构采用本文列出的常用的桩径与桩长时，一般情况下可以单独计算上部结构。

考虑到桩径与桩长对水工码头刚度影响最为显著，本文未考虑水工结构断面的差异对刚度造成的影响，工程中可根据实际的水工断面形式，参考本文的结论进行相应分析。

参考文献

[1]朱伯龙、张琨联.建筑结构抗震设计原理[M] .上海:同济大学出版社出版, 1994.

[2] 建筑抗震设计规范:GB 50011 -2010[S].北京:中国建筑工业出版社, 2016.

[3]胡聿贤.地震工程学[M].北京:地震出版社, 2006

[4]孙武、杨树标等.多质点弹性体系的地震反应分析 [J].河北建筑科技学院学报,2002

Analysis of Seismic Calculation of Superstructure

On Pile Foundation of Hydraulic Wharf

Zhou Xiangqin  CCCC THIRD HARBOR CONSULTANS CO.,LTD. Shanghai 200030

Abstract: In the seismic analysis of small buildings built on the hydraulic wharf, the hydraulic structure is often used as the fixed end of the superstructure, and only the superstructure is analyzed separately. In this paper, the elastic seismic response theory of multi-degree-of-freedom system is applied to analyze the influence of the stiffness of pile foundation on the superstructure's seismic response. Based on the model calculation of the upper two-story frame structure and the seismic analysis results of the upper structure under different pile diameters and lengths, the corresponding matching conditions of small buildings on the piled beam-slab wharf can be calculated separately are obtained.

Keywords: Multi-degree-of-freedom system; The pile diameter; Pile length; The lateral stiffness