浙江省湖州市第五中学教育集团 浙江湖州313000
摘要:辅助线是初中数学平面几何问题的重要一环,适当的添加辅助线,可以有效地解决几何问题.但对于学生来说如何添加辅助线是一大难题,本文以“截长补短”、“K型全等”、“旋转变换”为例,浅谈在三角形中如何从已知条件出发,引导学生发现题目中的特殊信息点,启发学生添加辅助线的方法,从而达到解题目的,鼓励学生一题多解.
关键词:辅助线、已知条件、三角形、一题多解.
一、截长补短
 例1:已知:
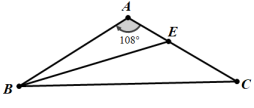
例1:已知:![]() 中,AB=AC,∠A=108°,BE平分∠ABC交AC于点E.求证:BC=AB+CE.
中,AB=AC,∠A=108°,BE平分∠ABC交AC于点E.求证:BC=AB+CE.
分析:此类求证一条线段等于俩条线段和的问题,学生已熟知“截长补短”的方法,但在具体应用中还是无从下手.本题启发学生从条件∠A=108°入手,结合AB=AC,先计算俩底角的度数,再尝试“截长法”,用圆规截取AB=BD,并连接DE.通过计算新的角度,找寻题目中的关于角或线段的等量关系.
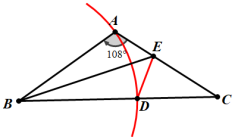 解:截取BD=AB,连接DE.
解:截取BD=AB,连接DE.
∵∠A=108°,AB=AC
∴∠ABE=∠C=36°
又∵BE平分∠ABE
∴∠ABE=∠DBE=18°
易证△ABE≌△DBE(SAS)
∴∠BDE=∠A=108° 从而∠CDE=180°-∠BDE=72°
∵∠EDC=180°-∠C-∠CDE=72°=∠CDE
∴CD=CE(等角对等边)
∴BC=BD+CD=AB+CE得证.
变式1:已知:![]() 中,AB=AC,∠A=100°,BE平分∠ABC交AC于点E.求证:BC=BE+AE.
中,AB=AC,∠A=100°,BE平分∠ABC交AC于点E.求证:BC=BE+AE.
分析:学生有了例1的基础,自然而然会先计算图中的各个角度,利用圆规截取BE=BD.这般“截长”后角度上并不存在等量关系,只能证明CD=DE,无法进一步证明CD=AE.这时候需要我们去启发引导学生进一步观察图中的特殊点E,落在角平分线上,可以利用角平分线的性质定理,进一步证明△AEM≌△DEN,从而得出结论.
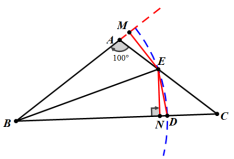 解:截取BE=BD,连接DE.作EN⟂BC,EM⟂AB
解:截取BE=BD,连接DE.作EN⟂BC,EM⟂AB
∵∠BAC=100°,AB=AC
∴∠ABE=∠C=40°
又∵BE平分∠ABE且EN⟂BC,EM⟂AB
∴∠ABE=∠DBE=20°,EM=EN.
∵BE=BD
∴∠BDE=∠BED=80° 从而∠CED=∠BDE-∠C=40°=∠C
∴CD=DE(等角对等边)
又∵∠EAM=180°-∠BAC=80°=∠BDE
易证△AME≌△DNE(AAS)
∴AE=DE(全等三角形对应边相等)
∴AE=CD
∴BC=BD+CD=BE+AE得证.
小结:由例1和变式1的加深练习,同学们可以基本掌握“截长补短法”,能理解相关辅助线为什么这样添加.启发学生通过题目中的角度和特殊点或特殊线段,结合相关数学重要性质,尝试添加辅助线以求完成求解目的.
二、K型全等
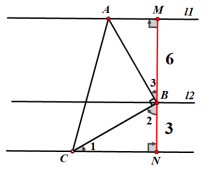
例2:如图,Rt△ABC中,∠ABC=90°,AB=BC,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3 .若l1与l2的距离为6,l2与l3的距离为3,求Rt△ABC的面积.
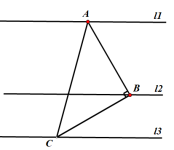 分析:题中的数量关系都与距离相关,而平行线之间的距离处处相等,都等于垂线段的长度.加上题目中提到的三角形是一个等腰直角三角形,同学们会联系到构造K型图.之前的练习中不难发现等腰直角三角形常常与K型全等放在一起,考察学生能否系统运用.这道题我们只需过点B作BM⟂AM,BN⟂CN即可.俩条垂线段的长正好是6和3.
分析:题中的数量关系都与距离相关,而平行线之间的距离处处相等,都等于垂线段的长度.加上题目中提到的三角形是一个等腰直角三角形,同学们会联系到构造K型图.之前的练习中不难发现等腰直角三角形常常与K型全等放在一起,考察学生能否系统运用.这道题我们只需过点B作BM⟂AM,BN⟂CN即可.俩条垂线段的长正好是6和3.
解:作BM⟂AM,BN⟂CN
由题可知BM=6,BN=3.
 ∵∠ABC=90°,BN⟂CN
∵∠ABC=90°,BN⟂CN
∴∠1+∠2=90°,∠2+∠3=90°
∴∠1=∠3(同角的余角相等)
又∵AB=BC
易证△AMB≌△BNC(AAS)
∴AM=BM=6,BN=CN=3
由勾股定理可得:AB=BC=![]()
![]()
变式2:如图,Rt△ABC中,∠A=∠2=22.5°,∠C=90°,BC=3,求AD的长.
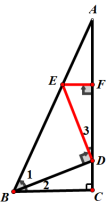
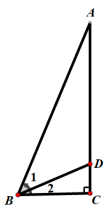 分析:这道题很短,22.5度这个信息点不常见,但能想到它是45度的一半.通过计算可以发现∠1=45°.从∠1=45°出发,它是一个特殊的角度,由此构造一个以∠1为内角的等腰直角三角形.若作DE⟂AB,虽然等腰直角三角形有了,但22.5度的信息点还是无法使用.所以我们作DE⟂BD.作好后出现一个新角∠3=22.5°,则△ADE为等腰三角形.
分析:这道题很短,22.5度这个信息点不常见,但能想到它是45度的一半.通过计算可以发现∠1=45°.从∠1=45°出发,它是一个特殊的角度,由此构造一个以∠1为内角的等腰直角三角形.若作DE⟂AB,虽然等腰直角三角形有了,但22.5度的信息点还是无法使用.所以我们作DE⟂BD.作好后出现一个新角∠3=22.5°,则△ADE为等腰三角形.
解:作DE⟂BD,EF⟂AD
由题可知∠1=180°-∠C-∠A-∠2=45°
 则∆BDE为等腰直角三角形
则∆BDE为等腰直角三角形
∴BD=DE,∠BDE=90°
从而∠3=180°-∠A-∠1-∠BDE=22.5°=∠A
∴AE=DE(等角对等边)
易证△BCD≌△DFE(AAS)
∴BC=DF=3(全等三角形对应边相等)
∵AE=DE,EF⟂AD
∴AF=2DF=6(三线合一)
小结:例2的距离,变式2的22.5度,都是已知条件中的信息点,而它们往往也是我们解题的突破点.俩题主要还是K型图与等腰直角三角形的综合运用.无论题目是直接点明等腰直角三角形,还是像变式2一样隐晦的给了我一个45度的角,在具体的题目中我们都可以这样联想.
三、旋转变换
例3:如图,等边△ABC中有一点O,连接OA,OB,OC.已知:OA=3,OB=4,OC=5,
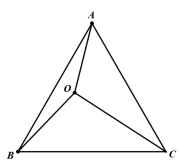 求∠AOB的度数.
求∠AOB的度数.
分析:现在长度为3,4,5的三边并不在同一个三角形中.由这个问题信息点出发,探索发现能不能通过某种方式把三边凑到一个三角形中.题目要求的是∠AOB的度数,尝试分割角来做.现在已经有一个等边三角形了,构造另一个等边三角形,利用手拉手模型解决问题.
解:将线段OB绕点B逆时针旋转60度至点D,连接OD,AD.
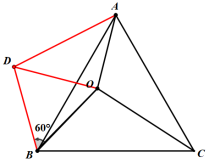 ∵旋转
∵旋转
∴OB=BD=4,∠OBD=60°
∴△BOD为等边三角形
从而OD=4,∠BOD=60°
∵△ABC为等边三角形
∴AB=BC,∠ABC=60°
∵∠ABC=60°=∠BOD
∴∠ABD=∠OBC
易证△ABD≌△CBO(SAS)
∴AD=OC=5
![]()
∴△AOD为直角三角形,即∠AOD=90°
∴∠AOB=∠AOD+∠BOD=150°
变式3:在例3的基础上,求四边形ADBO的面积.
分析:有了例3的基础,要去求四边形ADBO的面积就很简单了.线段OD将四边形ADBO分割成俩个三角形,△BOD是等边三角形,△AOD是直角三角形,分别求三角形的面积即可.利用等边三角形的面积公式求解一步到位.
解:![]() .
.
小结:例3和变式3用到的方法是旋转线段,基础图形里存在俩条线段相等时,可以联系到作旋转变换.利用旋转变换可以把一些位置上不相关的线段长度凑到一个三角形中.
四、综合运用
T:如图,等腰直角三角形ABC中,∠ADB=∠BAC=90°,AB=AC,∠ADC=135°,若∆ABD的面积为9,求AD的长.
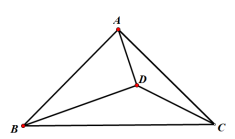 分析:题中提到的唯一数量关系是三角形面积为9,而我们要求的是AD长,正好为该三角形的一条直角边.我们介绍三种解题方法:①题中提到△ABC为等腰直角三角形,可以联系到作K型图求解.②题中提到AB=AC,可以联系到旋转变换.③要探索BD和AD之间的数量关系,可以截取一段DE=AD,再找寻BE与AD之间的数量关系.
分析:题中提到的唯一数量关系是三角形面积为9,而我们要求的是AD长,正好为该三角形的一条直角边.我们介绍三种解题方法:①题中提到△ABC为等腰直角三角形,可以联系到作K型图求解.②题中提到AB=AC,可以联系到旋转变换.③要探索BD和AD之间的数量关系,可以截取一段DE=AD,再找寻BE与AD之间的数量关系.
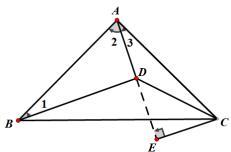 法1:作CE⟂AD交AD的延长线于点E
法1:作CE⟂AD交AD的延长线于点E
∵∠ADB=∠BAC=90°
∴∠2+∠3=90°=∠2+∠1
∴∠1=∠3(同角的余角相等)
又∵AB=AC
易证△ABD≌△CAE(AAS)
∴可设AD=CE=x,BD=AE
∵∠ADC=135° ∴∠CDE=180°-∠ADC=45°
则△CDE为等腰直角三角形,CE=DE=x
∴AE=AD+DE=2x=BD.
![]()
∴AD=x=3(x=-3不符题意,舍去)
小结:题中基础图形△ABC是个等腰直角三角形,而且题中已有一个Rt△ABD,再构造一个直角就有K型图可以利用了.
法2:将△ADC绕着点A顺时针旋转90度至△ABE的位置.连接DE.
∵旋转
∴可设AD=AE=x,∠EAD=90°,∠AEB=∠ADC=135°
∴△ADE为等腰直角三角形
∴DE=![]() ,∠AED=45°=∠ADE
,∠AED=45°=∠ADE
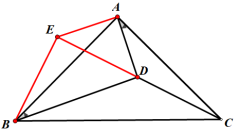 ∴∠BED=∠AEB-∠AED=90°
∴∠BED=∠AEB-∠AED=90°
∠BDE=∠ADB-∠ADE=45°
则△BDE为等腰直角三角形
∴BD=![]()
![]()
∴AD=x=3(x=-3不符题意,舍去)
小结:题中有一条件AB=AC,这个条件可以用来做旋转变换,加上在△ACD中有一个特殊角135度,旋转后连接DE,正好将135度的角分割成45度和90度,利用勾股得到三边关系就可以解决问题.
法3:在BD上截取DE=AD,连接AE.
∵∠ADB=90°,可设AD=DE=x
∴∠AED=∠EAD=45°=∠1+∠2
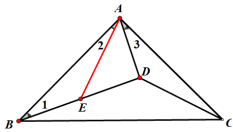 ∴∠AEB=180°-∠AED=135°=∠ADC
∴∠AEB=180°-∠AED=135°=∠ADC
又∵∠BAC=90°
∴∠2+∠3=45°
∴∠1=∠3
易证△ABE≌△CAD(AAS)
∴BE=AD=x(全等三角形对应边相等)
∴BD=BE+DE=2x
![]()
∴AD=x=3(x=-3不符题意,舍去)
小结:通过截取DE=AD的方式,构造了一个等腰直角三角形,由此产生了一个新的135度的角,结合题目中其他的条件可以证明俩个三角形全等,证得BE=AD,这样又找到了BD和AD的数量关系.
上述的三种解题方法都是由学生自主探究发现,在日常教学中有意识地引导学生从已知条件出发,找寻题中的特殊信息点,思维发散到相关的基础数学知识点,添加有效的辅助线已达成构造熟悉的数学模型.
五、总结
本文以几道具体的平面几何大题为例,简单介绍了三种常见的辅助线添法,在教学中读题时就要引导学生寻找已知条件中的特殊信息点,我们通过添加辅助线的方式,将一些关联性不大的知识点连成一线.在日常教学实践中,遇到需要添加辅助线的题目我们都可以引导教学,多次尝试后把课堂还给学生,让学生自己探索研究,交流分享,熟悉多种解题思路,以达成一题多解的训练目的.
参考文献:
[1].萨娜.2019.初中平面几何添加辅助线教学研究.[D].内蒙古师范大学.
[2].罗山.2020.辅助线在初中平面几何解题教学中的应用研究.[D].西南师范大学.
[3].莫云昭.2021.一道希望杯赛题的四种解法.[J].数理天地(初中版).
[4].徐鑫.2020.通过一题多解培养初中生数学思维能力的实验研究.[D].上海师范大学.
作者简介:钟华,本科,二级教师,研究方向:初中数学教学,单位:浙江省湖州市第五中学教育集团