变式训练在复习课中的应用——以《平移和旋转》章节为例

变式训练在复习课中的应用——以《平移和旋转》章节为例

樊婷

西安市经开第六中学 

【教材分析】

图形的轴对称、平移、旋转都是属于“图形与几何”领域中的图形变换。七年级学生学习的轴对称图形，已经掌握了学习图形变化的方法，为本节课打下了基础。本章学习的图形的平移与旋转是探索图形性质的必要手段，主要引导学生观察现实生活中的图形运动变化现象，培养学生观察、分析、归纳、概括的能力，为后期数学学习也做好铺垫。

【学情分析】

学生在七年级下册已经学过轴对称，积累了一定的图形变化的数学活动经验，通过探索轴对称图形的性质了解了研究图形变化的方法，同时有了一定的空间图形变化的能力，但是我班学生数学基础薄弱，空间想象能力不强，因此本节课例题以及变式相对便易，层层递进。

【学习目标】

1、建构本章的知识框架，对本章知识有一个系统的认识；

2、认识平移、旋转、中心对称，理解平移、旋转、中心对称的基本性质；

3、在研究平移、旋转的过程中，进一步发展空间能力。

【重难点】

重点：平移、旋转性质的应用

难点：平移、旋转性质的综合应用

【教学设计】

一、课前回顾

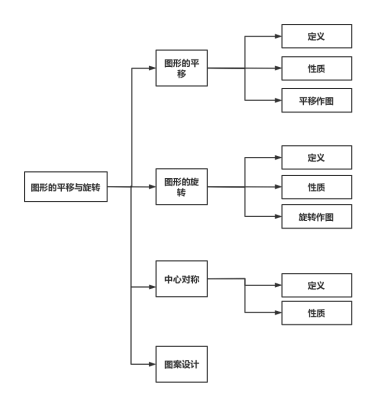   以问题串的方式提问，梳理本章知识点，形成思维导图。

设计意图： 建构本章的知识框架，对本章知识有一个系统的认识 ，掌握平移、旋转的性质，为后续做好铺垫。

二、典例精析  

例1、如图所示，在正方形网格中，为格点三角形。

（1）把沿方向平移后，点移到点，在网格中画出平移后得到的;

（2）把绕点按照逆时针方向旋转90°，在网格中画出转后的。

变式1：例1中的方格纸去掉，把绕点逆时针旋转60°，画出图形连接，，如图2，图中有哪些相等的角，有哪些相等的边？图中有哪几个等边三角形？

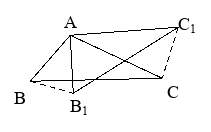
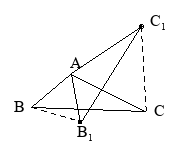
图2                       图3                  图4

变式2：例1中的方格纸去掉，把绕点逆时针旋转90°，画出图形连接，，如图3，图中有哪些相等的角，有哪些相等的边？图中有哪几个等腰直角三角形？

变式3：例1中的方格纸去掉，把绕点逆时针旋转°，连接，，如图4，图中有哪些相等的角，有哪些相等的边？图中有哪几个等腰三角形？

    图2换个角度，我们可以看成是两个等边三角形共顶点，图3可以看成两个等腰直角三角形共顶点，图4可以看成两个等腰三角形共顶点，由此可以得到如下变式。

变式4：（手拉手模型）等边和等边（或等腰直角和等腰直角或等腰三角形和等腰）共顶点，连接与，求证：≌

图5                          图6                图7

设计意图：例1利用平移、旋转的性质在方格纸中画出旋转后的图形，例1对于学生来说相对容易，同时促进学生对平移旋转性质的掌握；变式1和变式2是任意一个三角形旋转特殊得角度60°和90°，变式3是旋转任意°角度，让学生根据旋转得性质寻找相等的线段以及角度，进一步对旋转得性质得以巩固；变式4是在变式1，2，3的基础上换个角度审题，将一个图形的旋转转化两个顶角相等等腰三角形共顶点问题（即手拉手模型），层层递进，符合学生得认知发展规律，学生掌握效果较好。

例2、如图8，点是等边三角形内的一点，=3，，，求的度数。

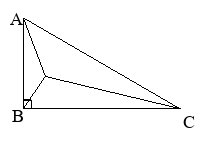
图8                                      图9

分析：、、比较分散，可以利用旋转得性质将三条线段集中。由变式1可知，把三角形旋转60°会出现等边三角形，进一步将边进行转化。

方法1：绕点逆时针旋转60°，则为等边三角形，转化到，为直角三角形，因此°。

方法2：绕点顺时针旋转60°。

方法3：绕点逆时针旋转60°。

方法4：绕点顺时针旋转60°。

归纳总结：如果图中有共点的相等线段（比如：等腰三角形、等边三角形、正方形、正多边形）可以利用旋转60°，将一些比较分散的点进行集中转化从而解决问题。

三、练习巩固

如图9，在中，为内部一点，连接，且，求的长度。

四、课堂小结

知识方面：

1、对第三章的知识建构了系统的知识体系，更加熟悉了平移旋转的性质；

2、了解了利用旋转的性质解决综合性几何问题

方法与技能：

体会化归，转化，旋转的数学思想方法

五、布置作业

必做：第三章知识进行梳理，以思维导图的形式呈现。

选做：对本节课中的题目进行整理。

教学反思：

本节课整个教学思路是先对本章知识进行梳理，再对典型例题进行不断的变形，以达到对本章的重点难点知识进行巩固、突破、升华。例1变形，由特殊到一般，由简到难，符合学生认知发展规律，取得了良好的教学效果。例2主要通过一题多解归纳总结利用旋转解决问题的条件和方法。由于课时的限制，本节课只呈现了部分利用旋转解决的几何问题。