象山县外国语学校
摘要:“一个定点,两个动点“型”折线段长的最小值问题一直在近几年很多中考题或者模拟题中频繁出现。初中阶段,最值问题一直是个难点也是一个重点。这类题型难度较大,要求学生具有较强的问题分析能力以及综合运用数学知识、数学思想方法解决问题的能力,是压轴类型中的一种题型,因此也常常让学生望而生畏。如何能将这类题型的方法固定化,常规化,化异为同就显得很重要。本文根据一道原创题中的线段最值问题,结合自己的理解,对这类最值问题的解题教学进行了深入的探究。
关键词:线段(和)最值;动点;将军饮马;平移法;一题多解.
一、基本模型:“将军饮马“模型
“将军饮马“问题是指动点在直线上运动,求此动点和两个定点间的线段和(或差)的一类最值问题。此类题型往往可以通过对称进行等量代换,从而转化成利用“两点之间线段最短”来解决。以下为范例(以两定点在动点所在直线的同侧并求线段和最小为例):
问题:在直线l上求一点P,使得PA+PB的值最小.
做法:作定点A关于直线l的对称点A′,连结A′B与直线l的交点即为点P.

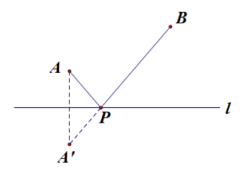
图1 图2
其实在我们遇到的很多题目中,并不一定是十分典型的将军饮马模型,而是在这个基础上进行稍作变动,例如有较多的题就是将两定一动求线段和的最小值改为两动一定求线段和的最小值.两动一定类型也有两种,一种是求定动+动动的值最小,另外一种是求动定+动定的值最小.以下我对第二种类型的题目进行分析讲解,并且一题多解.
二、问题解决
 题目:如图,直线AB与
题目:如图,直线AB与![]() 轴、
轴、![]() 轴分别相交于A(3,0),B(0,4),点M是直线AB上一个动点,将M向下平移2个单位长度得到N.
轴分别相交于A(3,0),B(0,4),点M是直线AB上一个动点,将M向下平移2个单位长度得到N.
(1)求直线AB的函数表达式;
(2)若线段MN与![]() 轴有一个公共点,求 M横坐标
轴有一个公共点,求 M横坐标![]() 的取值范围;
的取值范围;
(3)将AB沿过点A的直线折叠,使点B恰好落在![]() 轴上,
轴上,
折痕所在的直线交![]() 轴正半轴于点C,连结MC,NC,
轴正半轴于点C,连结MC,NC,
当△MNC的周长最小时,求此时点M的坐标.
答案:(1) AB所在直线表达式为![]()
(2) ![]()
(3)设点B的对应点为B′,连结B′C.
∵OA=3,OB=4
∴AB=AB′=5
∴OB′=5-3=2
设OC=m,则CB=CB′=4-m
由(4-m)2=22+m2可得m=![]()
∴C![]()
当△MNC的周长最小时,NC+MC最小,此时M′,C,N三点共线.
设M![]() ,则点N为
,则点N为![]() ,
,
M关于y轴的对称点是M′(-a,-![]() )
)
在此题第(3)小问的后续解答中,有以下几种解法:
 解法一:“将军饮马”法
解法一:“将军饮马”法
∵M′(-a,-![]() ),N
),N![]()
则直线M′N:![]() +3
+3
把点C![]() 代入得
代入得 ![]()
则M![]()
解法二:全等法
由于MF=EN=a,则此时△NCE≌△M′CF
∴CF=CE,即![]()
解得![]()
则M![]()
解法三:平移法
 将CN向上平移2个单位至C′M,则C′(0,
将CN向上平移2个单位至C′M,则C′(0,![]() )
)
作点C关于线段MN的对称点C“![]()
则点M就是直线C’C”与直线AB的交点.
∵直线C’C”:![]() +
+![]()
把M![]() 代入
代入![]() +
+![]() ,解得
,解得 ![]()
则M![]()
 此题的第一种解法其实就是在受到”将军饮马”的启发下进行了拓展,作了动点M的对称点M′,从而求让M′,C,N三点共线时即可.此种解法在本质上与“将军饮马“是相同的,但是又有一个动定转换的思维的飞跃。此题的第三种解法平移法,在两动点间距已知的题型中应用也是比较广泛的.
此题的第一种解法其实就是在受到”将军饮马”的启发下进行了拓展,作了动点M的对称点M′,从而求让M′,C,N三点共线时即可.此种解法在本质上与“将军饮马“是相同的,但是又有一个动定转换的思维的飞跃。此题的第三种解法平移法,在两动点间距已知的题型中应用也是比较广泛的.
下面我们应用类似方法来解决以下这个问题.
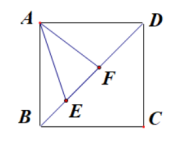
问题:如图,正方形ABCD的边长为3,E,F是对角线BD上的两个
动点,且EF=![]() ,则AE+AF的最小值为多少?
,则AE+AF的最小值为多少?
解法一:“将军饮马”法
将正方形绕点B顺时针旋转45°,建立以点B为坐标原点,
 以BD为x轴,则点A(
以BD为x轴,则点A(![]() )
)
设E(m,0)F(m+![]() )
)
因为E,F在x轴上运动,所以点A在直线y=![]() 上
上
作点E关于直线y=![]() 的对称点E′,则E′(m,3
的对称点E′,则E′(m,3![]() )
)
当E′,F,A三点共线,即将线段EF向右平移至线段E′F过
点A时,E′F的值最小.
∵ EE′=3![]() ,EF=
,EF=![]()
∴ E′F=![]() =
=![]()
此时我们会发现E′F的最小值是固定的,而且非常容易求.如果需要求出此时点E,F,的坐标,那我们只要求出直线E′F的解析式,再将点A坐标代入即可确定m的值.当然此题也同样可以用平移法来解决.
解法二:平移法
 连结CF,则在正方形中AF=CF
连结CF,则在正方形中AF=CF
将CF沿EF方向平移至EC′,连结AC′,
当点A,E, C′三点共线时,AE+AF最小且AC′即为最小值.
∵CC′=EF=![]() , HC′⊥BC,∠HCC′=45°
, HC′⊥BC,∠HCC′=45°
∴HC′=HC=BG=1
∴AG=4,BH=GC′=2
∴AC′=![]() =
=![]()
三、教学启示
数学中考是以定量评价、全面考察学生数学学习全过程的重要方式,而压轴题不仅注重考察学生对数学概念的理解,数学思想方法的掌握而且其对数学思考深度,探究与创新的水平及应用数学解决实际问题的能力有更高要求从而发挥甄别与选拔功能。最值问题就是其中一类压轴题。老师对综合题的教学绝不能就题论题,解一题是一题。我们更应该看到问题的本质,从源头去讲解,看看这个题能不能变“个案”为“类案”,能否研究出这类题的解题通法,也就是我们老师平时常说的举一反三。
综上,用“将军饮马“法求“一定两动”型折线段长的最小值,当两个动点都在线段上运动且间距固定时,采用构造动点关于定点所在直线的轴对称点,化折为直的方法求解;同时我们也可以用平移法,将讲个动点通过平移转化为一个动点,从而变成两定一动,转折为直进行求解。当然本文只是提供了一种相对稳定的样本,遇到一个新的问题时,还需要转化或分解问题,创新出更多精彩的运用.