基于模型认知解决晶胞相关的计算问题

基于模型认知解决晶胞相关的计算问题

曾聪

（广东梅县东山中学 广东 梅州 514000）

   晶胞相关的计算考察，是高中化学选择性必修2《物质结构与性质》的学习重点、难点，也是高考命题的热点、难点，综合考察了晶胞中粒子数的计算、立体几何知识和数学运算能力，对学生的学科综合素养提出了比较高的要求。认识、理解并掌握常见晶胞模型，能有效地帮助学生解决晶胞的相关计算问题。

一、晶胞密度的相关计算考察

晶胞的密度计算公式为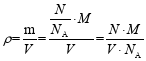。在计算出晶胞中所含粒子数后，根据提供数据及晶胞密度的求算公式，可以根据公式转换，求算晶胞密度、晶胞体积等未知数据。

[例1] [2020·全国卷Ⅱ，35(4)节选]一种立方钙钛矿结构的金属卤化物光电材料的组成为Pb2＋、I‒和有机碱离子CH3NH，其晶胞如图所示。若晶胞参数为a nm，则晶体密度为_______ g·cm‒3(列出计算式)。

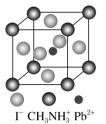
解析：由晶胞结构可知每个晶胞中含Pb2＋为1，含CH3NH为，含I‒为，即每个晶胞中含有1个Pb(CH3NH3)I3。Pb(CH3NH3)I3的相对分子质量为620，每个晶胞的质量为g，晶胞的体积为cm3。

则晶胞的密度。

答案：

二、晶胞空间利用率的计算方法

。因此，晶胞空间利用率的求解问题实际可分解为两个部分：①求晶胞中所含粒子的体积，②求晶胞的体积。

晶胞中的原子或离子属于球体，设原子的半径为r，由球体计算公式可求得单个原子所占体积为 πr3。

[例2] [2016·全国卷Ⅲ，37(5)节选]GaAs的密度为ρ g·cm‒3，其晶胞结构如图所示。Ga和As的摩尔质量分别为MGa g·mol‒1和MAs g·mol‒1，原子半径分别为rGa pm和rAs pm，阿伏加德罗常数值为NA，则GaAs晶胞中原子的体积占晶胞体积的百分率为_____________________________。

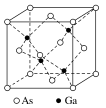
解析：本小题同时对晶胞密度和晶胞的空间利用率进行了综合考察。由晶胞结构可知每个晶胞中含有As原子数为，含Ga原子的个数为4，由晶胞密度可求晶胞的体积为。据题意可知As、Ga的原子半径分别为rGa pm和rAs pm，则晶胞中所含原子的总体积为。则GaAs晶胞中原子的体积占晶胞体积的百分率为：

。

答案：

三、典型晶胞结构模型的考察

    高中阶段所涉及的晶胞主要是立方晶体，也有涉及六方晶体，涉及晶胞参数的计算主要是正方体、长方体的体积计算知识。在这里，教学的重点和难点在于理清六面体边长和晶胞中原子半径之间的关系。限于篇幅关系，本文仅介绍各种晶胞中原子间的距离关系，不讨论晶胞的具体结构形成过程。

1．金属晶体的原子堆积模型

（1）简单立方堆积

简单立方堆积是正方体结构，属于非密堆积模型，晶胞中每个顶点正对原子的球心，每个边上的两个原子正好相切。

图1  简单立方堆积的空间构型

如图1所示，晶胞含有原子数为。设原子半径为r，则立方体的棱长a = 2r，，。则晶胞的空间利用率 = 。

（2）体心立方堆积

体心立方堆积是正方体结构，比简单立方堆积的利用率高，晶胞中体心的原子与体对角线上顶点的两个原子正好相切，且三个原子的球心处于同一条直线上。

图2  体心立方堆积的空间构型

如图2所示，晶胞含有原子数为。设原子半径为r，设立方体的棱长为a，则。晶胞的体对角线为，可得， 则。

则晶胞的空间利用率 = 。

（3）面心立方最密堆积

面心立方堆积是正方体结构，晶胞中面心上的原子与面对角线上顶点的两个原子的球心处于同一条直线上，面对角线上的三个原子正好相切。

图3  面心立方最密堆积的空间构型

如图3所示，晶胞含有原子数为。设原子半径为r，设立方体的棱长为a， 则。晶胞的面对角线为，可得， 则。

则晶胞的空间利用率 = 。

 [例3][2017·全国卷Ⅰ，35(4)节选] KIO3晶体是一种性能良好的非线性光学材料，具有钙钛矿型的立体结构，边长为a＝0.446 nm，晶胞中K、I、O分别处于顶角、体心、面心位置，如图所示。K与O间的最短距离为________nm。

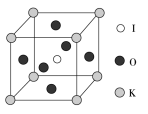
解析：由图可知，K、O分别位于晶胞的顶角和面心，形成面心堆积的结构，因此K与O间的最短距离为。

答案：0.315

（4）六方最密堆积

六方最密堆积有两种呈现方式，第一种方式是正六棱柱结构，底面为正六边形，每个原子都紧密堆积两两相切。底面中心的原子与顶点的六个原子间形成六个正三角形。体心的原子位于六棱柱的高的一半处，分别与对应的上底面、下底面的正三角形顶点的三个原子相切，形成两个正四面体。

图4  六方最密堆积的六棱柱空间构型

如图4所示，晶胞含有原子数为。设原子半径为r，设六棱柱的底面边长为a，侧棱高为2h，则a=2r，。底面正六边形的顶点连线，将底面分为六个正三角形，设正三角形的高为b，则由勾股定理可得。底面面积为。由晶胞体心原子与底面三个原子成正四面体，该正四面体的边长为a = 2r，可求得正四面体的高为，则六棱柱的高为

。则。

则晶胞的空间利用率 = 。

如图5所示，六方最密堆积的第二种呈现方式是六面体结构(四棱柱)，底面为菱形，底面的四个原子都正好相切，体心的原子位于四棱柱的高的一半处，但并非正中心。如图5所示，底面的1、2、3号原子与体心的4号原子均相切，形成正四面体结构。

图5  六方最密堆积的六面体空间构型

如图5所示，晶胞含有原子数为。设原子半径为r，设四棱柱的棱长为a，设四棱柱的高为2h，则a = 2r。。晶胞的底面菱形的高为，底面菱形的面积为。由晶胞体心原子与底面三个原子成正四面体，该正四面体的边长为a = 2r，可求得正四面体的高为，则四棱柱的高为。则。

则晶胞的空间利用率 = 。

[例4][2018·全国卷Ⅲ，36(5)节选]金属Zn晶体中的原子堆积方式如图所示。六棱柱底边边长为a cm，高为c cm，阿伏加德罗常数的值为NA，Zn的密度为g·cm‒3(列出计算式)。

解析：由图可知，金属Zn的堆积方式为六方最密堆积，每个晶胞中的含锌原子为12×＋2×＋3＝6个，每个晶胞的质量为 g。该六棱柱的底面为正六边形，边长为a cm，即底面的面积为6个边长为a cm的正三角形面积之和，由正三角形边长为a cm可得，正三角形的面积为，该底面的面积为，高为c cm，则晶胞体积为 cm3。则密度为。

答案：

（5）金刚石晶胞堆积

金刚石晶胞类型的堆积是正方体结构，在面心堆积的基础上，体心内在各条体对角线的四分之一处填充原子，体心共填充了四个原子。如图6所示，晶胞中两个碳原子的球心恰好位于体心对角线的顶点，体心对角线的四分之一处有一个原子，若体心对角线填充满原子，刚好为五个原子中心同处于体对角线上且五个原子刚好相切。

图6  金刚石晶胞堆积的空间构型

如图6所示，晶胞含有原子数为。设原子半径为r，设立方体的棱长为a， 则。晶胞的体对角线为，可得， 则。

则晶胞的空间利用率 = 。

[例5][2019·全国卷Ⅰ，35(4)节选]图(a)是MgCu2的拉维斯结构，Mg以金刚石方式堆积，八面体空隙和半数的四面体空隙中，填入以四面体方式排列的Cu。图(b)是沿立方格子对角面取得的截图。可见，Cu原子之间最短距离x＝________pm，Mg原子之间最短距离y＝________pm。

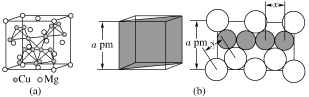
解析　设晶胞边长为a，Cu的半径为r(Cu)，Mg的半径为r(Mg)。由图(b)可知，面对角线的长度与4个Cu原子直径之和相等，即，则Cu原子之间最短距离为。由Mg以金刚石方式堆积可知，晶胞的体对角线的长度为，则Mg原子之间最短距离为。

答案：    

2．氯化钠晶胞堆积类型

NaCl晶胞类型的堆积是正方体结构，Na+与Cl‒紧密堆积。如图7所示，晶胞中Cl‒的堆积方式为面心立方堆积，面对角线上的三个Cl‒恰好相切，三个Cl‒的中心同处于面对角线上。Na+填充了氯离子之间的间隙，各边长上Na+与Cl‒中心处于同一直线，阴阳离子的球体相切。

图7  氯化钠晶胞堆积的空间构型

如图7所示，晶胞含Na+数为，含Cl‒数为，即含有4个NaCl。设Cl‒的半径为r1，Na+的半径为r2，设晶胞的边长为a， 则晶胞的面对角线为，则， 由可得。

[例6][2017·全国卷Ⅲ，35(5)节选]MgO具有NaCl型结构(如图)，其中阴离子采用面心立方最密堆积方式，X射线衍射实验测得MgO的晶胞参数为a＝0.420 nm，则r(O2‒)为________nm。

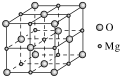
解析：O2‒是面心立方最密堆积，则面对角线是O2‒半径的4倍。设O2‒半径为，晶胞边长为a，则即，解得。

答案：0.148

四、总结语

笔者在教学过程中发现，晶胞相关的计算考察，是学生困惑较多、比较难理解、掌握的知识点，挑战较大。模型认知是化学学科核心素养维度之一，教师在教学过程中帮助学生认识、理解并掌握常见晶胞模型，学生在模型认知的基础上基于信息进行证据推理，理解晶胞中粒子的空间关系，则晶胞相关的立体几何计算、晶胞密度和晶胞空间利用率等计算问题迎刃而解。学生对晶胞认识、晶胞计算的能力得到提升，证据推理与模型认知素养也得到了促进发展。