测量与研究钠原子发光波列长度

测量与研究钠原子发光波列长度

覃振鹏

南宁学院 广西南宁

[摘 要]现阶段学者们偏向于对相干长度进行研究，但对波列长度的研究有所缺乏。本文基于迈克尔逊实验原理、原子发光理论和光产生干涉的条件，利用迈克尔逊干涉仪对钠原子干涉现象变化的边界情况进行观察，测量出干涉现象两边界处的位置，并根据光程差公式计算出钠原子发光波列长度，并与海森堡测不准关系进行分析对比，验证实验结果。

[关键词]钠原子波列长度;迈克尔逊干涉仪；实验

早在公元前四世纪，就出现了原始的原子学说，古希腊哲学家认为物质是由简单的、不可分割的基本单元[1]，即“原子”组成，但是原子物理学真正得到人们的重视是在十九世纪，原子物理学研究的领域和对象主要是物质的微观结构和运动情况，从而也揭示了宏观现象的本质，使得人们对微观世界有更进一步的了解。物理学家对光的规律及本质的探索经历了漫长、曲折且艰苦的发展过程，微粒说和波动说不断在历史的舞台上斗争，光的干涉及衍射现象无疑说明了光的波动性，通常情况下独立机械振源是连续的、相干的，容易出现干涉现象，但在光学中，由于原子的辐射不是连续不断的，所以光干涉的实现要满足一定的条件。美国物理学家迈克尔逊于1881年发明了迈克尔逊干涉仪，其精确度最高可达到波长的数量级，他曾用该干涉仪进行光谱线精细结构的研究，推动了原子物理的发展[2]。

原子之所以能发光，其实质是原子核外电子从高能级向低能级跃迁并向外辐射光子的过程，由于辐射具有随机性和复杂性，所以一个原子每次发光的持续时间是极短的，即发出的波列是有限的。而波列长度又制约着干涉现象的产生，由同一列光波分割出来的两列波不能在空间中某点相遇时，则无法产生干涉现象。关于“波列长度”这一概念，大部分的大学光学教材中对此概念通常一笔带过，无具体表述，学生缺乏对这一概念的认识，本文对波列长度的测量数值方面进行补充，同时增进学习者对干涉现象产生条件的理解。

一、研究背景与方法

迈克尔逊干涉仪因测量精确性高而广泛应用于计量技术及科学研究领域[3]，可用于棱镜和透镜质量、折射率和角度的检查和测量；依据该干涉仪的原理还可将其改进为其他形式的仪器；目前，大多数研究者将迈克尔逊干涉仪用于波长和折射率的测量，以及等厚和等倾条纹的观察和研究。

在2009年，李武钢、叶锦义和陈富真三人对原子发光持续时间进行研究，该实验选用钠光作为光源，进行牛顿环及劈尖实验，使用显微镜对视场中干涉图样的临界处进行观测，计算出钠原子发光的持续时间，并将实验值与运用测不准关系得出的理论值进行对比[4]，该研究的实验思路新颖，由于临界处并不是特别清晰，导致该位置的判定会存在一定的偏差，另外，可选用更精确的实验仪器进行研究；赵彦杰于2005年，用迈克尔逊干涉仪对钠光和激光的相干长度进行测量及比较，此外，得出两者波带宽度和辐射弛豫时间之比，将激光与学生较熟悉的钠光进行比较，利于学生对激光特征有更直观的认识和了解，并达到丰富大学物理实验内容的目的[5]；在2010年，梁少婷、拜璐等人利用该仪器精确、快速地对汞光源的相干长度进行测量，研究者们考虑到人眼限制性的问题，所以在该实验过程中使用CCD图像传感器，将干涉图样变化不清晰处进行放大，达到减少人为误差的效果，提高测量准确性，该实验方法还可推广到测量其他光源的波列长度[6]。可见，如今在光谱结构研究方面，学者们偏向于测量和研究相干长度，对波列特性还没有明确的定义[7]，原子发光波列长度领域的研究较缺乏。

此外，光学教材中很多是对原子发光的不连续性和发光持续时间进行描述，在讲述干涉现象产生的条件时，通常会对相干长度进行描述和推导，而往往忽略了波列长度的阐述，部分光学教程中虽有提及，但不够详细和全面，读者在理解时间相干性的过程中可能会感到疑惑，这方面的数据及测量方法需要进行扩充。

采用实验法进行探究，在实验过程中对干涉现象的变化的临界状态进行观察及测量；运用光程差公式计算出实验结果并得出实验结论，并运用海森堡测不准关系进行比较，主要从理论和人为等方面对实验中的误差进行分析。

二、实验原理及公式推导

1.实验原理

迈克尔逊实验的光路图如图2.1所示，S为光源，本实验使用平均波长为589.3nm的钠光源进行实验，M1和M2是两块相互垂直的反光镜，M2固定不动，M1可借助手轮进行微小的移动，G1和G2是两块与M1或M2成45度角、折射率和厚度都相同的平面玻璃板，二者相互平行，G1为分光板，背面为半透明表面，渡了银的薄层，其作用是使入射光分为强度几乎一样的反射光Ⅰ和透射光Ⅱ，形成两束相干光，G2为补偿板，用于补偿透射光Ⅱ的光程。

图 2.1 迈克尔逊干涉实验光路图

由光源发出的光束，经平面玻璃板G1分为两个光路，即反射光束Ⅰ和透射光束Ⅱ，反射光束Ⅰ经反光镜反射，又穿过G1，透射部分抵达观测点E，被反射的部分分散到空气中，不做讨论，若先不考虑补偿板G2

，则透射光束Ⅱ将垂直射入平面玻璃板M2，经反射后又穿过分光板G1的半透明表面，反射部分到达E处，透射部分同样分散到空气中，不讨论，到达E处的两束相干光将产生干涉图样。在此过程中，光束Ⅰ经过G1的次数为三次，而光束Ⅱ只穿过G1一次，加入G2后，光束Ⅱ到达E处之前也经过分光板G1三次，所以补偿板G2的作用就是补偿两光束由此产生的光程差，补偿后两路光的光程差可简化为在空气中的路程差。

2.实验公式推导

移动M1可调节两平行面间空气薄膜的厚度，根据薄膜干涉公式，有：

                      (2.2.1)

上式中，为膜的厚度，和分别为两种介质的折射率，为入射到平面玻璃板M1的入射角，是薄膜上下表面产生的半波损失，在迈克尔逊干涉实验中，两种介质均为空气，即，且上下表面无半波损失，所以光程差公式(2.2.1)可写为：

                         (2.2.2)

根据干涉条件，可得：

，干涉相长，产生亮条纹                (2.2.3)

，干涉相消，产生暗条纹              (2.2.4)

其中为干涉级，=1，2，3，…。

由式(5.2.2)可以看出，两波列的光程差不仅与空气薄膜的厚度有关，还与入射角有关，当光束垂直射入M1时，即入射角等于零时，两相干光束的光程差最大，所以干涉图样中心的干涉级次最高，当M1向M2’靠近时，空气薄膜的厚度减小，光程差减小，圆环向视场中心“陷入”，反之，当M1远离M2’时，空气薄膜的厚度增大，光程差增加，圆环由视场中心“冒出”。

现讨论干涉图样的中心圆环，即光束垂直射入M1的情况，将带入(2.2.2)式，得：

(2.2.5)

对于干涉图样中心而言，若反光镜M1移动了，光程差的变化与M1移动距离之间的关系为：

(2.2.6)

除了干涉中心外，两光束间的光程差的变化还与光束射入M1的入射角有关，在本文中忽略入射角的微小影响，可将其他区域光程差的改变简化为(2.2.6)式。

在本文实验原理部分提到光程差的变化量等于两倍的原子发光的波列长度，用式子表示为：

(2.2.7)

将式(2.2.5)与式(2.2.6)比较可得：

(2.2.8)

通过(2.2.8)式，可以得出波列长度与反光镜M1移动的距离的关系还可简化为:

(2.2.9)

三、实验步骤及数据处理

（1）调节好实验干涉仪器。首先点燃钠光源，使其经过装有十字叉丝的毛玻璃屏，使分光板G1、平面玻璃板M1、M2等高共轴，调节两反光镜后面的三个螺丝，使得动像与其中一个定像重合，随后继续调节两反光镜后面的螺丝，可观察到G1上出现干涉图样。

（2）确定干涉现象从无到有的位置。转动粗调手轮,会观察到视场中的干涉图样的视见度逐渐降低，直至观察不到干涉现象为止,缓慢转动微调鼓轮, 涉图样会重新出现在视场中，记录下干涉现象从无到有这一边界处M1的位置。

（3）确定干涉现象从有到无的位置。我们沿减小（增大）空气薄膜厚度的方向继续转动微调鼓轮，在此过程中会有一个时刻干涉现象会由有到无，记录下该时刻M1的位置为。

（4）重复进行实验步骤（2）、（3），记录下8组数据，如表3.1所示。

（5）关闭钠光灯，并收拾实验器材。

表 3.1 迈克尔逊干涉仪测量钠原子发光波列长度的实验数据（单位：mm）

由此可求出反光镜M1移动的平均距离：

mm

根据(2.2.9)式，钠原子的发光波列长度为：

mm

四、由海森堡测不准关系进行分析

与经典力学中粒子的位置和动量可以同时确定不同，在微观领域里，由于微粒本身固有的性质，即波粒二象性，微粒在空间中的位置要用概率波进行描述，而概率波只能给出该微粒在空间中某点出现的概率，所以任意时刻空间中微粒的位置都是不确定的，海森堡于1927年提出不确定性原理，该原理表明微观粒子的位置与动量不能同时具有确定的数值，其精确度有一定的限制，即，能量与时间也存在这种关系，即。根据能量与时间的不确定关系，可得：

（4.1）

上式中表示能量的不确定量，表示时间的不确定量，h为普朗克常量。

由，可得出：

（4.2）

将（4.2）式带入（4.1）式，得：

（4.3）

又（4.4）

（4.5）

将（4.5）式带入（4.3）式，得：

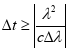                            （4.6）

上式可变为：

（4.7）

不等式左边表示波列长度（），本实验所用钠光的平均波长nm=589.3mm，c为光速，等于

m/s，钠光的谱线宽度范围在~nm之间，取nm=cm进行计算，将钠光波长和谱线宽度的数据代入（4.7）式，得：

mm

综上所述，根据海森堡测不准关系得出钠原子发光的波列长度的理论值为34.72745 mm。

五、实验误差分析与结果

1.实验误差分析

（1）迈克尔逊干涉仪是精密的光学实验仪器，使用时不经意地振动或灰尘会对实验的过程产生影响。

（2）本次实验的步骤（2）和（3）中要用肉眼对视场中的干涉图样变化的边界处进行判断，由于我们在分光板G1观察到的干涉图样小，在接近边界位置时视野中的图样可见度低，即图样并不清晰，会影响我们的判断，又由于人眼的局限性，对于微小变化的辨识是有限的，所以两边界位置和的确定是粗略的。

（3）光程差的变化量除了与反光镜M1移动的距离有关，还应该与光入射的角度有关，本实验中将入射角产生的影响忽略不计，从理论的角度而言，不是十分准确，导致误差的产生。

（4）实验仪器读数的误差，环境、仪器和个人等因素都可能对实验结果的准确度有一定的影响。

2.实验结果

普通光源的波列长度的数量级是微米，钠光灯的波列长度约为0.058 cm，但也可能达到几厘米，而激光的波列长度竟可达到千米数量级，波列长度越大，说明该光源的相干性越好。本文使用迈克尔逊干涉仪对钠原子的波列长度进行测量，通过观察干涉图样变化的临界状态，对两边界位置进行数据的测量，该实验计算出钠原子发光的波列长度等于32.42972 mm，通过海森堡测不准关系得出理论值为34.72745 mm，实验值与理论值有些许的差别，但两者都为同一数量级，考虑到实验仪器、环境、人为等因素的影响，允许存在一定范围的实验误差，总而言之，在误差范围内实验值与理论值基本吻合，实验结果具有有效性，将理论与实验相结合，达到预期效果。

六、小结

通过本文的研究，可以加深读者对“波列长度”这一概念的认识、让读者进一步理解光产生干涉的条件和原子能级跃迁，对波列长度的测量及研究也有一定的参考意义，不管是在波列长度数值上的补充，还是迈克尔逊干涉仪测量范围的扩充上都有一定的作用。

参考文献：

[1] 褚圣麟. 原子物理学[M]. 北京：高等教育出版社，1979.

[2] 姚启钧. 光学教程[M]. 北京: 高等教育出版社, 2014.

[3] 刘小平，邹长伟，梁枫. 普通物理实验 光学部分[M]. 南宁：广西人民出版社，2013.

[4] 李武钢. 用干涉法测原子发光持续时间[J]. 广西物理，2009，30(4)：29-31.

[5] 赵彦杰.用迈克尔逊干涉仪比较钠光和激光的相干长度[J].山东轻工业学院学报，2005，19(3)：61-63.

[6] 梁少婷. 利用迈克尔逊干涉仪测量汞灯光源的相干长度[J]. 科技传播，2010，183-184.

[7] 光谱超精细结构模型研究新进展[J]. 科学通报，2008：507.

[8] 隗嘉城. 浅谈原子能级跃迁中的实现与产生光子的问题[J]. 科技风，2019：203.

基金项目：南宁学院 2021 年校级科研项目自然科学类“钠、汞和钨发光波列长度的测量与研究”（编号：2021XJ07）研究成果。

作者简介：覃振鹏（1989.05—），男，壮族，广西桂平人，研究生，讲师，研究方向：大学物理实验教学与研究。