(潍坊工程职业学院,山东 青州 262500)
作者简介:赵文英,1992.11 ,女,山东临朐,汉,高职数学教学,助教,硕士研究生
摘要:微分方程来源于实践,是现代科学技术中分析问题和解决问题的有力工具。介绍微分方程的几个应用实例,将实际问题抽象成微分方程模型,通过求解微分方程,用得到的解来分析实际问题。读者可从中感受到应用微分方程的理论和方法解决实际问题的魅力。
关键词:微分方程;温度冷却;人口预测;传染病传播
1 微分方程数学模型应用
1.1 温度冷却问题
把一杯加热到![]() 的牛奶,放到
的牛奶,放到![]() 的恒温环境中冷却,求牛奶温度的变化规律。根据牛顿冷却定律:一个较周围热的物体温度为
的恒温环境中冷却,求牛奶温度的变化规律。根据牛顿冷却定律:一个较周围热的物体温度为![]() ,忽略表面积以及外部介质性质和温度的变化,它的冷却速率与该物体的温度
,忽略表面积以及外部介质性质和温度的变化,它的冷却速率与该物体的温度![]() 与周围环境的温度
与周围环境的温度![]() 的差成正比。在冷却过程中,设牛奶在时刻
的差成正比。在冷却过程中,设牛奶在时刻![]() 的温度为
的温度为![]() ,物体冷却的速率就是牛奶温度对时间的变化率
,物体冷却的速率就是牛奶温度对时间的变化率![]() 。于是可得下列微分方程
。于是可得下列微分方程
![]() (1)
(1)
其中,![]() 为比例常数,上式右边出现负号,是因为随着时间
为比例常数,上式右边出现负号,是因为随着时间![]() 的增加,温度
的增加,温度![]() 在减小,即当
在减小,即当![]() 时,
时,![]() 。
。
利用分离变量法求解上述微分方程初值问题,得![]() ,两边同时积分
,两边同时积分![]() ,可得
,可得![]() ,将初值
,将初值![]() 代入得所求温度的变化规律为
代入得所求温度的变化规律为![]() 。设定
。设定![]() ,利用MATLAB软件绘制图像。
,利用MATLAB软件绘制图像。
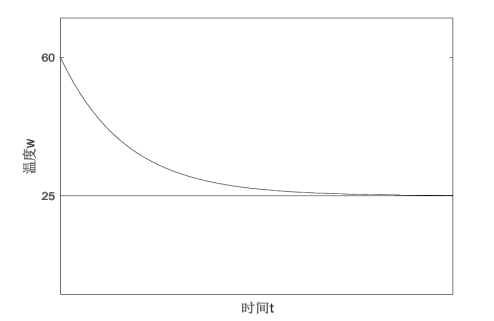
由上图看出,牛奶温度的冷却是按指数规律变化的。随着时间![]() 的增加,温度的下降由快变慢,最终趋于环境温度
的增加,温度的下降由快变慢,最终趋于环境温度![]() 。
。
1.2 人口预测问题
1798年,英国著名人口学家马尔萨斯(Malthus)提出了马尔萨斯人口模型
![]() (2)
(2)
其中,将人口看做是连续时间![]() 的连续可微函数
的连续可微函数![]() ,
,![]() 表示初始时刻(
表示初始时刻(![]() )的人口,
)的人口,![]() 表示单位时间人口增长率。
表示单位时间人口增长率。
上述方程可以用分离变量法求解,分离变量得![]() ,等式两边求积分
,等式两边求积分![]() 可得人口与时间的关系为
可得人口与时间的关系为![]() 。当人口增长率
。当人口增长率![]() 时,人口将按指数规律无限增长。这显然是不符合实际的,人口不可能无限增长下去,资源环境都是有限的。不过,虽然马尔萨斯人口模型不适合描述、也不能预测较长时间的人口变化过程,但是用它作短期人口预测是可以的,因为在短时间内,人口增长率
时,人口将按指数规律无限增长。这显然是不符合实际的,人口不可能无限增长下去,资源环境都是有限的。不过,虽然马尔萨斯人口模型不适合描述、也不能预测较长时间的人口变化过程,但是用它作短期人口预测是可以的,因为在短时间内,人口增长率![]() 是常数大致成立。
是常数大致成立。
考虑到增长率随时间变化,在人口增长到一定数量后,环境条件、自然资源等因素对人口的增长起着阻滞作用,并且随着人口的增加,阻滞作用越来越大。于是,有了下列![]() 方程:
方程:
![]() (3)
(3)
其中,![]() 是(理论)上
是(理论)上![]() 的增长率,
的增长率,![]() 表示资源和环境所能容纳的最大人口数量,
表示资源和环境所能容纳的最大人口数量,![]() 表示人口增长率函数。
表示人口增长率函数。
求解上述微分方程,得
 。
。
设定参数![]() ,
,![]() ,
,![]() ,
,![]() ,利用MATLAB软件对1970-2021年中国人口总数进行数值模拟(数据来源于中国统计年鉴2021和年度统计公报)。
,利用MATLAB软件对1970-2021年中国人口总数进行数值模拟(数据来源于中国统计年鉴2021和年度统计公报)。
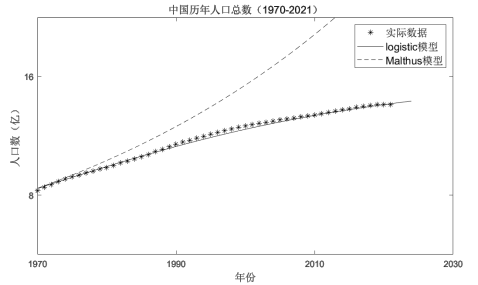
从上图可以明显看出,Malthus模型在较短的时间内可以预测人口数量,长时间内则不再可信。而![]() 模型在较长的时间内都可以比较准确地预测人口的数量。
模型在较长的时间内都可以比较准确地预测人口的数量。
2 结语
以上介绍了微分方程的三个应用实例,涉及微分方程在物理学、人口学、生物医学方面。除此之外,微分方程的发展极大地推动了力学技术、电子技术等诸多领域的发展,为它们提供了关键技术支撑。
参考文献:
[1]陈凤英. 高等数学(工科类)[M]. 北京: 北京师范大学出版社, 2021: 140-158.
[2]姜启源. 数学模型(第五版)[M]. 北京: 高等教育出版社, 2019: 141-188.
[3]史诗洁. 浅谈常微分方程在数学模型中的应用及其数值模拟[J]. 教育教学论坛, 2020,(45):122-123.