巧用转化思想解高考数学题

 巧用转化思想解高考数学题

韦娅妮

广西省柳州市融安县浮石镇初级中学 广西省柳州市 545402

摘要: 转化思想是将未知的、陌生的、复杂的问题通过演绎归纳转化为已知的、熟悉的、简单的问题，从而使问题得到顺利解决的数学思想，巧用转化思想的培养也是一种能力的培养，这是数学课程标准提出的总体目标之一,是高考考察的一个重点,因此巧用转化思想解高考数学题应该得到重视，提高解题的效率与准确率。本文将通过巧用转化思想解高考数学题来研究，“数”与“形”的相互转化、生疏问题向熟悉问题转化、难问题转化为易问题、代换的思想方法、观察并挖掘题目隐含条件。转化思想可以提高解题的效率与准确率，帮助学生在高考中取得较为优异的成绩。

关键词:  转化思想；高考数学题；巧用方法 

1.引言

何为数学转化思想，布卢姆在《教育目标分类学》明确指出：数学转化思想是“把问题元素从一种形式向另一种形式转化的能力”,它可以从文字描述向图形转化，或从复杂的问题转化成简单的问题等。 本文从教材背景、实际生活、新课程改革背景等多角度进行研究,而前人是从单一的背景进行研究。本文不足之处：1.查阅资料有限。 2.对题目的分析不够全面。本文从“数”与“形”的相互转化、生疏问题向熟悉问题转化、难问题转化为易问题、实际问题转化为数学问题、代换的思想方法、观察并挖掘题目隐含条件进行研究。在高考中，巧妙地使用转化思想解题，提高解题的效率与准确率，帮助学生在高考中取得较为优异的成绩，具有研究的实际意义。

2. 巧用转化思想解高考数学题

2.1“数”与“形”的相互转化

数形结合思想简而言之就是把数学中的“数”和数学中的“形”结合起来解决数学问题的一种数学思想。应用数形结合的思想可以解决以下问题：①集合问题②函数问题③方程与不等式的问题④三角函数问题⑤线性规划问题⑥数列问题⑦解析几何问题⑧立体几何问题。

例1（2012重庆高考理2）不等式的解集为（    )

解：将分式不等式化为整式不等式得

且

令

解得

使用穿针引线法将“数”转化为“形”得：

                      图1

由图形可知原不等式的解集为故答案选

点评： ①具体步骤是从右往左、从上往下、依次穿根、奇穿偶不穿，奇是指某一个根为奇数个时，偶是指某一个根为偶数时。在数轴上方的部分大于0，在数轴下方的部分小于0。

②类似的题目：(2010全国理5)不等式的解集为（    ）

解题的基本思路：明确题中所给条件和所求的目标，分析已给出的条件和所求目标的特点和性质，理解条件或目标在图形中的重要几何意义，用已学过的知识正确的将题中用到的图形用代数式表达出来，再根据条件和结论的联系，利用相应的公式或定理等。

例2（2012江苏高考理12）在平面直角坐标系，圆的方程为，若直线上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，则k的最大值是____。

解：依题意化为标准方程为：

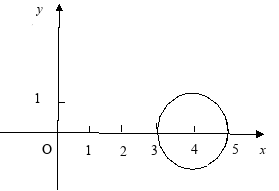
得到该圆的圆心为，半径为1.

在直角坐标系作图如下：

   “形”变“数”

1为半径的圆与圆C有公共点

只要圆心到直线的距离

解得的最大值是。

点评：①由圆心在直线上，则可以设圆心为，已知圆的半径为1，可得此圆的方程为，与圆C的方程有交点，就可以联立组成方程组，根据求出的取值。

 ②类似的题目：(2012天津高考理14)已知函数的图象与函数的图象恰有两个交点，则实数k的取值范围是____。

例3（2011年全国理5）已知角的顶点与原点重合，始边与轴的正半轴重合，始边在直线上，则（    ）

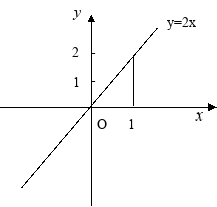
解：根据题意画图

“数”转化为“形”

直接根据题意作图，在直线上取特殊点（1,2）构造直角三角形.

                       图3

   “形”变“数”

代入值得

故答案选 点评:如果用代数方法解题，根据条件可以求出，根据隐条件求出，根据求出。用此方法计算比较繁琐，做题效率低。

数学题目成千上万，不可能全部做遍，但可以通过一定量的练习掌握它们的解法，就拥有了会解大量数学题的能力。解题能力实际上是一种创造的思维能力，这种能力的关键是能否细心观察，运用过去所学的知识将生疏问题转化熟悉问题。

【参考文献】

[1]汤服成.中学数学解题思想方法[M].桂林：广西师范大学出版社，2006.9-189.

[2]叶立军.初等数学研究[M].上海：华东师范大学出版社，2010.55-65.

[3]华建忠.巧用转化思想妙解数学问题[J].中学数学，2012，（10）:80.

第 1 页 共 4 页