用大单元眼光看一节初中数学课的核心素养——以湘教版数学七年级教材《列代数式》一节为例

用大单元眼光看一节初中数学课的核心素养——以湘教版数学七年级教材《列代数式》一节为例

徐健 

桂林市逸仙中学

摘要：一节好的数学课是渗透数学核心素养的课。数学的核心素养支撑起了学生思考的空间。我们可以按照2022版《义务教育数学课程标准》所提供的三个方面来看一节数学课的核心素养。

关键词：大单元数学核心素养  列代数式  数学语言  数学抽象  数学建模

引言

自2022版《义务教育数学课程标准》实施以来，对新版《义务教育数学课程标准》的研究和实践成为科研热门，它也是指导普通教师实施、评价、改革日常教学的指南针。在一线执教的老师应当借助2022版《义务教育数学课程标准》作为衡量教学的标尺、工具，认真研究使用教材，发现当前使用教材的价值，将数学核心素养渗透到教学当中去。

一、注重教学内容与核心素养及大单元主线之间的关联

2022版《义务教育数学课程标准》在课程实施部分中指出，“探索大单元教学”，“推进单元整体教学设计”，“分析主题-单元-课时的数学知识和核心素养主要表现”，“整体设计，分步实施，促进学生对数学教学内容的整体理解与把握，逐步培养学生的核心素养”。因此教师在教学过程中，不仅要注重具体内容与核心素养之间的关联，还要注重内容主线与核心素养发展之间的关联。

具体到一节数学课中，不但要考虑本节课内容与核心素养之间的关联，还要考虑它与大单元主线以及它与核心素养之间的关联。教师要用大单元的眼光看教学内容与核心素养之间的关联。

二、从三个方面看初中数学的核心素养

2022版《义务教育数学课程标准》的课程理念就是要帮助学生逐步形成适应终身发展需要的核心素养，数学核心素养既是理念又是课程目标。在新《课标》中明确指出，初中阶段核心素养主要表现为：抽象能力、运算能力、几何直观、空间观念、推理能力、数据观念、模型观念、应用意识、创新意识。

新《课标》指出，数学课程要培养的学生核心素养，主要包括以下三个方面：（1）会用数学的眼光观察现实世界；（2）会用数学的思维思考现实世界；（3）会用数学的语言表达现实世界。

因此，我们可以从上述三个方面来思考一节数学课的核心素养价值。

三、以大单元眼光看教学内容与主题主线

湘教版数学七年级教材《列代数式》一节是“数与代数”领域下、属于“数与式”主题的内容，是本册课本的第二章第二课时，是学生在有理数的运算和用字母表示数的基础上学习列代数式表示简单数量关系的一节课。通过本节课的学习，学生实现由数到式的过渡与升华，是学习整式加减的基础。藉由本节课，学生从数式进入代数式的学习，也就是说学生的思维从数转入字母（代数式）。

四、以大单元眼光看教学内容与核心素养

湘教版数学七年级教材《列代数式》一节通过探究六边形图形规律、下定义、用代数式表示语句、列代数式等四个内容，在学习过程中，培养学生的观察能力、几何直观、抽象能力、数学语言表达能力，初步培养学生的模型观念、应用意识。

五、用数学的眼光观察现实世界

数学的思考开始于用数学的眼光观察现实世界，抽象出事物所具有的特点，并用数学的语言加以描述，进而发现问题，经过推理、计算得出数学结论，解决问题。

《列代数式》一节的第一个内容就是让学生通过探究图中所示六边形的规律，用数学含字母m的式子将这个规律表示出来。学生所经历的心理过程，是将所观察到的图形规律转换成数字规律、再以字母（代数式）的形式表达出来。

课本引导学生首先发现第一个图形是六边形，再由第二个图形发现火柴棍数量不是每次增加6，而是增加5。当这个图形按着这样的规律“增长”时，火柴棍的数量该怎样描述更为简单就成为一个数学问题。学生可以借助上一节内容《用字母表示数》来把所观察到的数字规律转化为式子表示出来，于是得到[6+5(m-1)]根（如图1）。

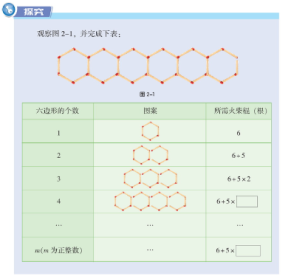
图1

把握教材内容所导向的核心素养，我们可以将这一问题改变为一题多解的形式，让学生再次经历这一过程，形成巩固。在发现了第1个图形之后的所有图形中，火柴棍的数量都包含数字5，就可以引导学生观察思考在第1个图形中是否包含数字5，整个图形的规律又可以怎样描述。如果学生观察到第1个图形的火柴棍数量为6=1+5，那么第m个图形火柴棍的数量就可以表示为(1+5m)根（如图2）。

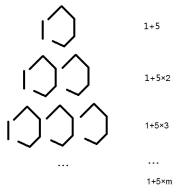
图2

[6+5(m-1)]和(1+5m)两个式子对于学生来说，暂时是两个不同的答案，但却是基于观察、抽象得到的事实表达，它们可以帮助学生回归到客观世界的丰富表现中去，激发学生在数形结合的领域从不同角度进行数学思考。

教师要合理利用课本资源，培养学生的抽象能力、几何直观，能将观察、思考的结论准确地表达出来。

六、会用数学的语言表达现实世界

数学的语言表达，不是感性的表达，而是一种带有思考的理性的表达。数学的语言表达可以分为两类，一类是描述观察到的事物特征（即抽象），二是用于推理计算证明。教师要教会学生把通过观察得到的事物特征用数学语言表达出来，进而进行推理计算证明。

课本在对代数式给出定义之后，给出的例1和例2两个例题，就是让学生形成用数学眼光去观察和思考的观念。关注问题中相关联的量，关注问题（情境）描述中重要的数学关系描述。

在例1中（如图3），三个语句都是对相关计算的文字描述，是在数式的基础上，对相关字母运算的描述，其重点在于学生能把语言的描述准确地翻译成代数式。学生对基本运算的准确表达，是培养学生模型观念和应用意识的铺垫。

图3

学生能自觉运用数学语言进行描述和表达，是学生有数学思维活动的一种体现，也是可以进行交流合作的前提。借助课本P61页的习题第1题，学生可以自信地进行正确的观察、思考和表达。

图4

教师要引导学生理解代数式的定义，会用文字语言、符号语言、图形语言将观察、思考的结论表达出来，培养学生的抽象能力和应用意识。

七、会用数学的思维思考现实世界

数学的思考，是基于对现实世界的观察、抽象后，去掉无关因素，只对抽象得到的数学符号语言进行推理、计算，得出结论，从而达到提出问题、分析问题、解决问题这一目的的思考。因此，关注与问题相关的量就十分重要。

课本在例2中（如图5）以价格问题和行程问题为例，引导学生列代数式。教师在教学过程中可以借助画图、列表等形式向学生展示各数量之间的关系。无论采取何种形式，最终的目标就是让学生透过表示数字的字母x、y、v看到它们所表示的量之间的关系，即总价=单价×数量，时间=路程÷速度，由能够用字母表示数进阶到能用代数式表示各数量之间的关系，发现事物本质的联系。

图5

以大单元的眼光来看，列代数式是整个第二章的基础，前面衔接有理数的运算及用字母表示数，后继为代数式的化简求值运算做铺垫。更为重要的是，学生能用数学的眼光和语言来表达观察到的事物特征和数量之间的关系，就能为下一章《一元一次方程》打好基础，因为用一元一次方程的方法解决实际问题就是发现问题中数量之间的等量关系，利用事物之间的本质联系去解决问题。

通过例2我们看到列代数式是进入代数部分的门槛，学生由此进入以字母为表征的代数部分的学习，后续的代数部分的课程都要用代数式揭示各量之间的本质关联。

教师要培养学生的观察归纳能力，抽象能力，渗透模型观念，能用数学语言把事物本质的特征和联系表示出来。

八、大单元教学设计理念带领回归数学本质

数学的本质是研究空间形式和数量关系的科学。一节好的数学课不只是教会学生怎样解题，更需要在教学过程中将课程内容中所包含的核心素养呈现出来。借助大单元教学的眼光，从不同角度可以看到课程内容中潜在的价值，把一节课的效益最大化。

教师应当研究、运用2022版《义务教育数学课程标准》，更新理念，设计教学，把数学课变成增长数学知识、锻炼数学能力、培养数学素养的好课。

参考文献：

1. 《“理解为先”模式下初中数学大单元教学设计的思考与应用》，庄河，泉州第十六中学，知网，基础教育，分类号G633.6；

2.《大单元教学：实现数学教学设计与学科素养的有效对接》，屠卓娅，浙江省杭州市萧山区回澜初级中学，知网，基础教育，G633.6；

作者简介：徐健（1979-），男，壮族，广西桂林人，中学一级教师，从事中学数学教学工作