三种预报模型在基坑沉降预报中的精度比较

三种预报模型在基坑沉降预报中的精度比较

姚翔

速度时空信息科技股份有限公司，江苏 南京 210000

摘 要：基坑工程的安全稳定对企业及社会具有十分重要的意义。本文在某一工程实例的原始观测数据序列的基础上，分别利用灰色模型、灰色神经网络组合模型以及小波优化的灰色模型对基坑的沉降进行预报。结果显示：在短期稳定的原始数据序列中，灰色模型的预报精度最高，组合模型虽然具有一定的优势，但在原始数据序列不足的情况下也难以发挥其模型特点，获得较高的预报精度。

关键词：基坑；沉降监测；预测模型；组合模型

城市人口的不断增加，导致城市的土地资源越来越紧张，基坑和深基坑工程在近几十年来应用的越来越广泛。由于基坑工程的施工环境多样，施工工艺复杂，施工事故多有发生，全国各大中城市都有发生各种各样的基坑变形、塌方事故，造成巨大的人员和财产损失。因此，基坑工程的变形监测以及预报工作变得越来越重要，通过对基坑的自动化、全天候实时监测，并利用预报模型进行沉降预报，预防可能发生的安全问题，为城市建设保驾护航。

1、模型简介

1.1灰色系统模型

灰色系统理论是1982年由邓聚龙教授在关于“含未知数系统的控制问题”的学术报告中首次提出的，主要为解决含未知数系统的控制问题，后来，经过不断的补充和发展，灰色系统理论在自然科学、社会科学等许多领域发挥了非常重要的作用，具有非常广阔的发展空间。

灰色系统理论进行预报，是把原始数据看作是在时间发展的基础上相应发生变化的过程。GM（1,1）预报模型是灰色预测理论中应用十分广泛的预测模型。

1.2灰色神经网络组合模型

灰色系统在进行变形预报的过程中主要优势是可以通过掌握的一部分信息来预报未知的信息达到对系统整体的认识。灰色系统对样本的要求比较低，但本身也存在着不可避免的缺点：（1）灰色系统对平滑序列的预测效果非常好，对波动序列的预报效果就会大大减低。（2）灰色系统模型是基于微分方程，对信息的处理能力，误差处理能力和非线性拟合能力比较差，而且并没有考虑到误差的反馈调整问题，使得计算的精度比较低。

和灰色系统理论不同，BP神经网络的学习能力和误差校正能力是十分突出的，神经网络通过反复的训练在一定程度上可以满足任何条件下的非线性映射，此外，BP神经网络还具有很强的并行处理、自适应能力。

但是，BP神经网络在预测过程中需要大量的样本数量和充分的训练。而在实际的生活、生产实践中，信息不完全的问题是十分普遍的，前期观测数据的缺失和不足，会导致BP神经网络的学习不够充分，无法得到非常理想的内部结构。而神经网络又无法区分黑色和灰色信息，因此在数据处理的过程中，忽略了很多确定信息的应用，从而导致精度的减低。

灰色系统可以通过相关的算子建立数学模型，来反应灰色数据系列可能的变化状态和发展过程，对于小样本数据的处理效果特别明显，这点可以大大弥补神经网络样本需求量大的弱点。同时，灰色系统还可以弱化数据的随机性，避免数据序列中的特殊点对结果造成的影响，弥补了神经网络中数据不广泛导致的泛化能力减弱以及特殊数据点对神经训练造成的干扰等缺陷。

1.3小波优化的灰色模型

小波分析是20世纪80年代开始得到发展的新兴学科，经过一段时间的发展，在很多方面得到了广泛应用。小波分析是形状可变、窗口大小不变的时频局部化的分析方法，具有非常好的自适应性。

小波去噪是小波分析中的一个关键环节。在观测数据序列中，比较平稳的信号或者是低频信号通常是一般变形信号，而高频信号中通常含有噪声信号。因此，在数据处理中，需要对含有噪声的信号进行分解，剔除噪声信号，然后再重构恢复信号。

小波分析是形状可变、窗口大小不变的时频局部化的分析方法，具有非常好的自适应性。对观测数据进行去噪一般有以下几个步骤：（1）小波分解。对需要处理的数据选定一种小波，确定小波分解的层数，进行分解。（2）小波分解高频系数的阈值量化处理。确定小波分解后的阈值，然后可以从高频信息中获取一些有用的信号。（3）小波重构。降噪处理后再经过小波重构恢复原始信号。

通过建立小波优化的灰色预测模型，先利用小波优化获得的数据，再将处理后的信息作为灰色预测模型的初值，提高预报的精度，满足工程需要。

2、实验分析

工程选取某市城际地铁一期工程，车站是该城际轨道交通一期工程的中间站。位于两条路的交叉路口，方向为南北向。车站结构为地下两层岛式车站，车站标准段宽19.2m、高13.21m、长276.0m，底板埋深为14.78m，小里程端盾构井深16.719m，大里程端盾构井深16.338m。车站主体标准段为双层双跨单柱箱型框架结构，部分为双层三跨双柱箱型框架结构。

基坑沉降监测点位的布设情况如下：

基坑周围地表沉降监测点布设于基坑外30m范围土体，沿基坑纵向每15～20米布设一个沉降监测点，按D1，D2，……，D32命名，同时布设5个沉降监测断面，每个断面10个沉降点。周边地表沉降监测点共计80个地表沉降监测点。具体点位分布如图1所示。

图1 观测点位示意图

2.1 GM（1,1）预报模型

选取DB11号点第10期至第19期共十组数据来进行预报和验证。因为灰色GM（1,1）模型需要的历史数据至少为4个，经过对不同步长的预测效果的研究，决定利用第10期到第15期作为模型建立数据，第16期到第19期数据作为预报数据。预测结果如表1所示。

表1 GM(1，1)预报值与观测值对比表

2.2灰色-神经网络组合模型

由于灰色系统模型和BP神经预报模型各有其优点以及不足之处，因此，将灰色系统和BP神经网络模型想结合，进行观测值的处理和预报。

采用第6期至第15期的观测数据来建立模型，来预报第16期到第19期的观测值。预报结果如表2所示。

表2灰色神经组合模型预报值与观测值对比表

2.3小波优化灰色模型

在进行小波优化的过程中，主要是运用到MATLAB软件中的小波分析工具箱wavemenu。在命令行输入“wavemenu”。在选择一位小波工具后，导入所要进行处理的数据，然后选择小波类型和分离的层数。这里，我们选用第6期至第15期观测值进行小波降噪，根据试验，选用db6函数，分解层数为2层。

利用去噪后的数据作为GM（1,1）预报的初值，进行预报，所得的第16期至第19期的预报情况见表3。

表3 小波优化GM(1，1)预报值与观测值对比表

2.4 各模型精度比较

在对三种模型分别进行沉降预报之后，将各模型的预报值与原始观测数据进行对比，如图1所示。

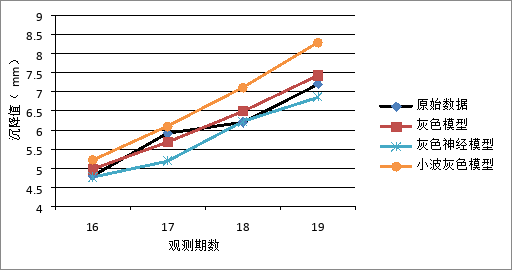
图1 各模型预报值与观测值对比图

3、结论

由各预报模型的预测精度可知，在同一工程条件下，各个模型的预报精度会有较大的差别。在DB11号点的预报过程中，灰色模型的预报精度整体较高，这也符合了灰色模型在短期、稳定的沉降过程中预报精度较高的特点。灰色神经网络和小波优化灰色模型虽然在模型上具有一定的优势，部分阶段的预报精度非常优秀，但是在没有足够原始数据序列的情况下也难以发挥其模型优势。因此，在实际工程中，应该根据工程特点选择合适的预报模型，才能更好地维持基坑工程的安全运行

参考文献：

[1]邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002:15-20.

[2]华博深.灰色组合模型在基坑监测数据处理中的运用[D].成都:成都理工大学,2012:20-22.

[3]齐长鑫,汪树玉.灰色系统模型在坝基位移预测中的应用[J].水利学报,1996,9(5):49-52.

[4]Lee In-Mo, Lee Jeong-hark. Prediction of Pile Bearing Capacity Using Artificial Neural Networks. Computer and Geotechnies, 1996, 18(3):189-200.

[5]文莉,刘正士.小波去噪的几种方法[J].合肥工业大学学报(自然科学版).2002(25):2-4.

[6]田胜利,周拥军,葛修润.基于小波分解的建筑物变形监测数据处理[J].岩石力学与工程学报.2004(15):2639-2642.