高速电机轴承刚度对转子振动特性的影响分析

高速电机轴承刚度对转子振动特性的影响分析

罗大辉1,2,,张登平1，2,,屈仁英1，2,陈思洁1，2

（1.贵州航天林泉电机有限公司，贵阳 550081；

2.国家精密微特电机工程技术研究中心，贵阳 550081）

摘要：高速电机由于其高速性、高功率性、低重量性等优势，在航空航天、武器装备、深海探测等领域的应用逐渐广泛，但高速电机的高速属性对转子的振动特性具有较高要求，若激励频率与转子本身固有频率接近，电机会产生共振现象，严重时影响装置的正常运行。本文使用有限元软件对不同轴承刚度下的转子系统进行固有频率、临界转速、分析，获得了通过改变转子轴承刚度避开高转速共振带的结论。

关键词：转子轴承刚度振动特性

1前言

高速电机转速高、体积小、能够有效降低同功率下的重量，同时由于其高转速特点可与原动机直接相连、省去了中间的减速机构、降低了动力传递过程中的过多额外损失，提高装置能量利用率，以上众多优点使高速电机一直倍受关注。但发电机的高速化对发电机转子的振动特性具有较高要求，高速化提高了电机本身的激励频率，若外界的扰动频率或自身激励频率与转子本身的固有频率一致，会导致设备共振，严重时可能引起转子扫膛，甚至转子轴的变形断裂。为防止研发的发电机在使用过程中出现上述情况，本文使用ANSYS Workbench对不同轴承刚度及转速下的转子系统进行固有频率及临界转速分析，研究表明，发电机转子的振动特性与转子的轴承刚度息息相关，可通过改变转子的轴承刚度，错开共振带。

2研究现状和趋势

在研究轴承轴承刚度对转子振动影响的模型中，若轴承的刚度小于转子刚度，则转子可以简化为刚体，对应的轴承可以简化为弹簧和阻尼器的并联组合，通过求解系统的微分方程组来研究转子系统的动态行为。高速电机转子和其他机械转子类似，运行转速正在逐步提高，体积小、机动性高的高速电机作为燃气轮机驱动的电源，可带来重大经济效益；从长远看，高速电机的单位功率和工作效率等方面的优势可以提高整个工业产值并降低成本。

但在很多工程实际应用中，对发电机转子的动力学问题时，大多限于转子临界转速的确定，且在计算中把轴承简单的作为绝对刚性支承计算模型进行分计算，从理论分析，上述处理方法过分的简化了工程问题，不能体现转子轴承刚度对转子振动带来的影响。因此，大功率高速电机转子的振动特性研究研究意义重大。

3高速电机转子结构

本文主要研究大功率高速电机转子的振动特性，因此定子部分在此不再赘述，转子采用两端轴承支撑的结构。所研究的发电机转子案例如图1所示，转子由两个挡圈、磁钢、以及最外圈的护套组成。其中磁钢的材料为稀土永磁材料钐钴Sm2Co17，密度8400kg/m3，弹性模量1.17E11Pa，护套和挡环均为高温合金GH4169，密度8240kg/m3,弹性模量1.99E11Pa，泊松比0.3。

图1发电机转子结构图

4转子动力学分析

4.1动力学理论模型

模态是转子系统的固有振动特性，表示了其在各频率下的动态响应特性。相应的振动模态参数是决定发电机转子动力学特性的重要参数，得到了轴承—转子系统的模态参数之后，即可建立一个动力学模型，并由此计算发电机转子在实际荷载作用下的响应，根据响应结果对轴承刚度进行必要的修改。轴承刚度K的定义如式（1），F表示轴承内外套圈之间产生单位的相对弹性位移量所需的额外载荷。

(1)

轴承支撑下的发电机转子系统动力学模型可简化为左右支撑等效为弹簧和阻尼器的组合：

动力学方程为

                        (2)

式中  

M——质量集合矩阵

C——阻尼集合矩阵

K——刚度集合矩阵

—节点位移列向量

—节点速度列向量

—节点加速度列向量

—节点外载荷列向量

上述各集合矩阵中，分别包括了球轴承对发电机转子的支承刚度、球轴承阻尼以及球轴承对发电机转子球轴承—转子系统动力学特性的影响。当球轴承—转子系统不受外载荷时，其自由振动方程为：

                          (3)

求解式(3)的特征值和特征向量，即可求出球轴承—转子系统的各阶固有频率和振型。利用振型叠加的方法可以求出球轴承—转子系统在外力作用下的位移响应。以球轴承为支承的球轴承—转子系统的阻尼作用较弱，此处不予考虑，即C = 0。则轴承支撑下的发电机转子系统的无阻尼自由振动的运动方程为：

                             (4)

简化后，只需求解式(4)的特征值和特征向量,即可获得轴承支撑下的转子系统的固有频率和振型。

4.2仿真模型建立

为便于仿真的进行，将轴承支撑下的转子系统进行简化，主要包括：将轴承简化为弹性支承，按照受力情况，只考虑径向刚度；忽略转速对轴承刚度的影响；忽略球轴承内部弹流润滑油膜的影响。仿真中将护套两端轴肩圆周表面分别插入轴承连接，设置相应的2维度刚度值，并为轴承连接设置远端点，边界条件设置中，对轴承连接相关的两个远端点进行约束，限制其轴向位移和轴向转动。

图2为转子系统的三维网格划分，其中网格节点数为49381，单元数10065。

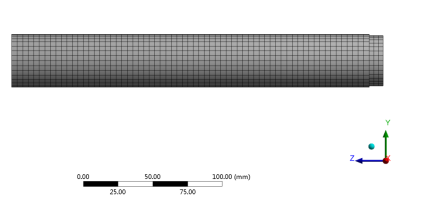
图2转子网格划分

4.3仿真结果及分析

4.3.1无转速状态

本小结分析中，进行无转速状态下转子固有频率的变化趋势，从而为进一步的动力学分析，如谐响应分析提供理论支持。取轴承刚度2.0e7N/m～6.0e7 N/m分别计算相应的模态频率，取前8阶结果如表1，可知低阶频率随着轴承刚度的提高，转子系统固有频率也相应提升，考虑到实际应用中发电机转子系统的轴承刚度会随轴承的种类，型号，预紧力大小而变化，在需要改变转子模态频率时可更改相应参数进行频率偏移，防止共振的产生。

表1不同轴承刚度下转子系统模态频率

4.3.2高转速状态

本文研究的大功率高速电机，拥有较高的旋转速度。当转子旋转时，由于离心力的作用，模型的刚度会变大，但由于离心力的方向不断变化，所以会导致模型并不稳定，这又使模型的刚度变小。因此分析旋转模型的固有频率时，需考虑转速的影响。

因本文研究的高速电机转子额定转速为90000r/min，本节选取10000 r/min，50000 r/min，90000 r/min三个转速点进行分析，轴承刚度选择1.0e7N/m、1.5e7N/m、2.0e7N/m三个点。从图1和表2中可知，当刚度为1.0e7N/m时，一、二、三阶模态频率下均存在临界转速，若以20%为临界转速共振带，则四阶临界转速共振带为63101r/min～94652r/min，刚好和额定转速重合，所以该轴承刚度的选取不满足设计要求。表3和表4 展示了轴承刚度为1.5e7N/m、2.0e7N/m时的模态参数，可知随着轴承刚度的增加，转子系统的模态频率逐步增加，同时临界转速在各个模态阶数中的个数逐渐降低，轴承刚度为2.0e7N/m时的最大临界转速为39471r/min，不在额定转速范围内，满足设计需求。

表2轴承刚度1.0e7N/m频率转速特性

表3轴承刚度1.5e7N/m频率转速特性

表4轴承刚度2.0e7N/m频率转速特性

5结论

本文以某大功率高速电机的实际设计问题为例，通过有限元软件对轴承支撑下的转子系统进行了模态分析，获得了转子系统在不同参数条件下的固有频率及临界转速等模态参数，复现了轴承轴承刚度对转子模态频率具有较大影响的理论，对本文研究的高速转子系统，轴承刚度的选择不当会造成转子系统

的共振，在不考虑其他因素的条件下，可选择刚度为2.0e7N/m左右的轴承作为发电机转子和定子之间的连接元件。

参考文献：

[1]大型汽轮发电机组轴系不对中振动的研究动力工程[J]，王延博，2004振动工程学报；

[2]超高速电主轴球轴承—转子系统动力学性能的研究[D]，李松生，2006，上海大学；

[3]轴承—转子系统动力学[M]，虞烈,刘恒等，2001，西安:西安交通大学出版社；

[4]高速旋转机械振动[M]，晏砺堂、朱梓根、李其汉等，1994，国防工业出版社；

[5]ANSYS Workbench有限元分析实例讲解[M]，周炬,苏金英，2015，人民邮电出版社；

[6]基于球轴承刚度计算的电主轴结构分析与优化[D]，李娜，2011，华中科技大学；

[7]发动机转子—滚动轴承系统的振动性能研究[J]，袁茹、王三民、任平珍，1999，机械科学与技术；

基金项目：脉冲发电机(编号：2006WZ0002)、内置式起动发电一体机研制（编号：XXXX-2022-114）