借力多元表征，提升运算能力——《两位数乘两位数的笔算乘法》人教版和苏教版的比较研究

借力多元表征，提升运算能力——《两位数乘两位数的笔算乘法》人教版和苏教版的比较研究

徐英

江苏省常州市新北区新桥实验小学  213000

摘要：计算教学是小学数学的关键内容，教师在教学过程中要沟通算理和算法。文章结合三年级下册的《两位数乘两位数的笔算乘法》的教学，结合不同版本的教材，阐述如何在计算中迁移算理和算法，提高学生的计算能力。

关键字：多元表征；计算算理；算法；运算能力。

如何培养学生的运算能力是小学数学教学的重要内容和基础。“运算能力”是《义务教育数学课程标准（2011年版）》提出的应当注重发展的十项素养之一，培养运算能力有助于学生理解运算的算理，寻求合理简洁的运算途径解决问题。基于对运算能力的思考，本人将研究视角指向了《两位数乘两位数的笔算》，它是整数乘法，乃至小数乘法的核心内容。它与三年级上册的两三位数乘一位数的方法有明显的差异，是学生自主类推多位数乘多位数的笔算的方法，是学生认知结构由旧知到新知的一次拓展，更是乘法笔算学习的一次跨越。在执教这一节课时，本人经历了学习、对比、实践和反思，尤其在借力多元表征上感触颇多，以下将思考过程呈现出来促使更多的思考和探索。

一、两种版本《两位数乘两位数笔算》教材简析

1、笔算的前沿、单元、后续的知识结构体系：

2、课时比较分析

人教版：先是创设情境，整体感知，利用学生已有的学习经验得到数量关系：每套的本数×套数=购买的总本数。然后利用点子图引导学生圈一圈，画一画，算一算，借助几何直观找到计算的方法。最后竖式呈现完整的过程和每一步的含义和由来，沟通口算方法的算理和竖式计算的算法。

苏教版：苏教版充分利用情境，提出问题：一共有多少个？引导学生从情境图中找到解决问题的方法：借助学生认知的经验和已有的数学知识数量关系，感悟口算可以先算什么在算什么的思路。然后立足情境，理解算理，连接笔算竖式，掌握算法。

二、两种版本《两位数乘两位数笔算》教学逻辑

1、课时教学的共性逻辑：购物生活情境中形成需求，经历口算（图示直观拆积与拆和）——数学抽象竖式笔算（结构关联）

2、教材设计的个性路径：

在学生生活经验相一致的基础之上，人教版突出前期学习经验与思维经验的积累，苏教版则从来没有出现过点子图设计，通过观察箱子图对应口算的两种方式方法。

3、不同的图像表征，达成不完全相同的目标：

人教版：点子图，数形结合，直观具象

苏教版：箱子图，观察视角看到思维，半抽象

人教版：

苏教版：

三、《两位数乘两位数笔算》的教学启示

基于两种教材的分析和比较，在教学过程中应该互相融合，从学生的认知特点和原有的基础出发，在苏教版教材中融入点子图的设想：适当渗透、适时出现，丰富一种数学学习的思维视角，积淀一种方法路径，积累一种学习经验：从知道——应用，优化教学设计。以下是本人的实践——《借力图案表征，立足情景，沟通“法”“理”》：
师：（出示情境图：有12箱南瓜，每箱14个）冬去春来,又到了播种的季节。小熊维尼和小猪正在清点百亩森林里丰收的情况，为今年的播种做好准备。

师：罗宾打包了好多迷你南瓜，让我们一起来看一看！现在小熊遇到了一个数学难题，一共有多少个？你们愿意帮助它吗?

师：你会列式解答吗？师板书:14x12)

师:大约是多少？你是怎么估的？(板书:一百多)

(一)初步探究
师：仔细观察这个算式，和我们之前学习的有什么不同？

师：（揭题）今天我们一起来学习两位数乘两位数。看到这个课题，你最想在课堂上学会什么？

师：刚才同学们都关注到了计算的方法，其实除了要关注怎么算？还要关注为什么这样算？现在请同学们拿出手中的学习单看向活动一：

活动一：

想一想：你打算怎样解决14×12，把你的想法记录在方框里；

圈一圈：在图中表示出算式中的含义，有需要的可打开学习锦囊。

说一说：在小组里交流自己的想法。

学生尝试独立完成，师走进学生了解学生完成情况。小组交流。

资源一：

苏教版主要突出审图的育人价值，转化路径为观察中习得口算的方法，学会观察、学会分析、学会思考。

资源二：

提供的学习锦囊主要是突出了人教版点子图的优越性，引导学生从乘法的意义出发，把箱子图抽象成点子图，利用数形结合的方法探究两位数乘两位数。

资源呈现，并列交流：

①拆积：12可以分成2个6、6个2、3个4、4个3等

14×6＝84     84×2＝168

指出：12拆成2个6，先算6个14，再乘2。

②拆和：整十数和一位数

2×14＝2810×14＝14028＋140＝168

指出：把12拆成10和2，先算10个14，再算2个14，最后加起来。（板书）

师：回顾一下，最初我们遇到的问题解决了吗？方法不同，你能透过它们不同的方法之间看到什么相同的地方吗？

生：先分再和；转化；数形结合。

师：说得真好，能透过算式看到隐藏在它们后面的规律，真了不起，正如他们所说，都经历了先分后和的过程。这样就把我们没学过的新知识转化了已经学过的旧知识。而画点子图的方式可以更直观的帮助我们思考。

师：比一比，你更喜欢哪一种？

生：第二种，计算方便；所有情况都能分成整十数和一位数，更具有一般性。

师：那你能用这种方法再来算一算14×12么？订正好后和同桌说说你的想法。

（设计意图：这节课主要关注学生算理和算法的理解，所以设计了箱子图和点子图找到两者之间的联系。通过活动，给学生独立探究的空间，让他们利用几何直观，以点子图为抓手，找到解决两位数乘两位数的一般方法。方法是多样的，但与主题图意更接近的是第二种，让学生充分内化，为后面的笔算算法做铺垫。）

（二）探究笔算方法

谈话：其实，老师看到有的同学已经想要列竖式算一算了，想的可真好。下面请同学们试着利用竖式笔算14×12的积，同时思考竖式笔算的时候应该先算什么，在算什么，然后小组讨论交流。

呈现资源，序列交流：

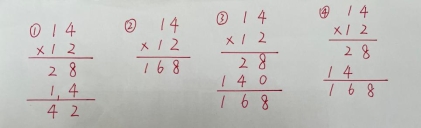
师：哪一种更能完整的体现我们的计算过程？你是怎么想的，谁来说一说。

生：第三种方法把这个算式把分与和的过程表达很清楚。

师：你是怎么想的？请你到黑板上来演示一下你是怎么算的。（生演示算法。）

师：3、4号作业对比总结：写了0就表示140个一，不写就是14个十，不影响最后的结果，为了简洁，一般就不写0。不写0，4为什么写在2的下面？

生：因为是十位上1乘4，表示4个十。

（三）沟通联系

师：仔细观察你有什么发现？

观察发现是先算2×14，再算10×14得14个十。要写在十位上。横式和竖式和点子图都是先算14×2，第二步算14×10，最后加起来。

师：和十位上的4对齐，也就是做到了相同数位对齐，是啊，数学上的乘法计算，就是把相同单位的数进行累加的过程。那么到现在14×12怎么算以及为什么这样算，清楚了吗？

指出：原来这三种算法形式不一样，道理却是一样的。（理清算理）

（设计意图：在沟通笔算和口算算法的联系时，做到算理和算法的融合，做到点子图、横式算法和竖式算法的统一。在竖式呈现后，及时把含义、由来与点子图进行横向沟通，让学生知其然，更知其所以然。在理清算理和算法之后更一步呈现点子图的直观作用，它体现出的数形结合是竖式里的每一步，增加学生的探索欲望。）

其实本节课我主要是想要融合两种教材，取其优点扬长避短。三项资源的呈现（点子图、横式、竖式）有效沟通算理和算法之间的联系。在教学中，一方面对竖式计算中每一步积的由来与口算横式和点子图勾连，使学生能深刻理解先算2个14是两箱的个数，再算10个14是10箱的个数，最后要把它们合起来才能解决这个问题。另一方面是解决教学重难点第二层积的位置可以直接写在十位上，理由是用十位上的1乘14得到140，也就是14个十，所以积的末尾要和十位上对齐。所以在教学笔算的过程中，要充分利用情境与点子图，做到数形结合，在计算时眼中有“数”，脑中有“形”，数形结合沟通理法。

四、结束语

教材是承载知识的载体，是体现课程标准的要求和内容的主要文本资源之一。基于小学生数学的学科性质和年龄特点，小学生数学运算能力的培养应注重已有经验创设情境，数形结合理解算理，灵活运用口算笔算和估算。借力情境表征、图像表征和符号表征等多元表征，提高学生的运算能力。为此，本人特意通过这次的实践书写教材比较研究，找到两种教材背后的精心编制和深刻意图，备好每一节课解读好每一份教材。利用不同的教材可以帮助教师贯通知识的联系，加深对教材的理解，从教学走向研究。

参考文献

[1]蒋敏杰,潘小福.运算能力的培养要紧扣“理”“法”“境”——以《两位数乘两位数(不进位)笔算》教学为例[J].小学教学设计,2020,(35):27-29.

[2]吴莉彬.“两位数乘两位数笔算乘法”各版本教材的比较研究[J].数学学习与研究,2020,(04):152-153.

[3]陈梦雅,杨灵巧.利用点子图理解两位数乘两位数笔算的算理[J].小学教学(数学版),2021,(04):54-55.

1