初中数学发散思维能力的培养—以平行四边形为例

初中数学发散思维能力的培养—以平行四边形为例

胡晓琪

厦门市松柏中学        361012

【摘要】思维能力是学生学习数学的重要能力，因此在日常教学中，教师不仅要重视对学生基础知识、基本技能的培养，也要重视学生思维能力的培养。在不断改革的教学中，如何培养学生发散思维能力是需要教师去思考的。文章以平行四边形为例分析初中数学发散思维能力的培养策略。

【关键词】发散思维能力；培养策略

初中阶段是学生发散思维能力快速发展的重要阶段，学生的可塑性较强，教师在教学中要能够正确地引导学生掌握一定的发散思维能力，在初中数学课堂教学中，教师要多给学生提供足够的机会让他们学会对知识融会贯通、举一反三，在训练他们能力的同时更好地提高学生的思维创新能力。本文就如何培养初中数学发散思维能力，提出了以下可操作策略:

一、设置思维发散点，提供学习支架

培养学生的发散思维能力需要有一个发散点，也就是从一个或几个知识点出发，通过多角度、多形式、多层次的命题变换，对学生进行发散思维训练，从而灵活地掌握各个知识点，进而达到知识同化性迁移的目的，提高初中学生数学发散思维能力。例如，在平行四边形性质教学中，可以设置如下例题。

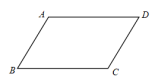例题1：如图，在□ABCD中，

①若∠A＝135°，则∠B＝°，

∠C＝°，∠D＝°；

②若∠A－∠B＝40°，则∠C＝°，∠B＝°；

变式1.连接对角线AC，BD交于点O，

①若AO=6，BO=5，则CO=，BD=.

②若CO=3cm，△ABC的周长为15cm，则□ABCD的周长为cm.

通过一题多变，不仅让学生加深对平行四边形性质的理解，也培养学生的发散思维能力，在课堂上，教师可以以小组的形式，让学生自主命题，并上台展示，说明命题的设计意图，在此过程中训练学生的发散思维，让学生学会举一反三，在后续平行四边形的综合里也能够熟练运用知识，在复杂题目中抽离出基本的模型，联想到熟悉的知识点。

二、巧设问题情境，助力思维发散

教师要通过创设教学情境，设置一连串富有启迪思维而又层层递进的问题，有的放矢。教师还要鼓励学生质疑，主动探究，独立思考，启迪思维发散，在探究中体会数学乐趣，在合作中提高抽象思维能力与数学应用能力。

例如在特殊平行四边形的探究中，将平行四边形的边或角特殊化，小组合作探究特殊平行四边形的性质和判定，构建知识框架。

教师提问：我们知道平行四边形的性质判定跟角和边有关，若将角特殊化，例如将平行四边形的一个内角的度数变为30°或45°或60°或90°，此时的四边形是什么四边形，这个四边形有什么特征？请同学们探究。

学生探究完角特殊化，教师再追问还可以探究什么？边的特殊化。

   通过问题设置，启发学生思考探究特殊四边形的性质和判定，培养学生发散思维和创新思维。

三、引导学生自主探究，形成思维多样化

目前在初中数学教学中，不少教师依旧采用传统的灌输式的教学方法传授理论知识。这种传统的教学方式不利于活跃学生思维，教师要引导学生开展自主探究活动，鼓励学生求知，找寻问题答案，在探究中学会思考和分析，自主探究让学生参与到知识的生成过程中，深入理解知识，提升创新思维的能力，培养学生良好的学习习惯。

例如，在学习四边形性质时，教师开展师生互动，准备几组互相全等三角形（任意三角形、一般的直角三角形等），让学生拼出平行四边形和特殊平行四边形，在操作过程中加深了四边形定义的理解。让学生度量边、角、对角线，观察探究四边形的性质，一方面激发了学生的学习兴趣，另一方面加深了学生对知识点的理解。

教师可以组织学生深入交流，引出平行四边形和特殊平行四边形的性质，小组进行讨论，让学生自主学习平行四边形和特殊平行四边形的性质。这不仅加强了师生、生生之间的交流，还调动了学生的学习积极性。学生在体会知识的生成过程中，感受到成功解决问题的快乐。在实践中创造和发展数学知识，在实践中获得和享用数学知识，学生的发散思维能力在探究中得到提高。

通过平行四边形的探究总结研究思路，让学生先自主研究特殊平行四边形的性质等，也可以利用研究思路探索“梯形”的定义、性质、判定。可将探究其余四边形的题型放在课后作业里，让学生课下进行探究，为后续学习其他四边形提供研究思路和学习方法。

四、构建知识体系，明晰思维条理

复习课教师常常将知识碎片化，没有形成体系，学生很难在问题中找到清晰的条理，不利于学生发散思维能力的发展，所以要充分利用好复习课，将碎片化的知识连点成线，连线成面，连面成体，将知识系统化。知识的系统化呈现可以是教师设置好思维导图，也可以鼓励学生自己动手整理各个部分知识中的概念、公式，寻找它们之间的联系，画出思维导图，自主构建清晰的数学知识理论体系。耳听不如眼看，眼看不如手动，学生亲自动手实践，锻炼学生发散思维，培养动手操作能力。

五、鼓励学生多角度思考问题，助推思维扩散

一题多解是数学学习中常见的思维模式，需要学生对知识点理解透彻，掌握知识点之间的联系，多角度思考问题，不断寻找解决问题的方法，助力于思维的发展。解题方法的多样化不仅有利于学生积极思考，相互交流分享，培养思维多向性能力，而且有利于促进学生创新能力的发展。

例如：“如图，E，F是平行四边形ABCD的对角线BD上的点，．请你猜想：AE与CF有什么关系？并对你的猜想加以证明.”容易猜想得到AE∥CF，AE=CF。

解法1：边、角相等联想到三角形全等，故先利用平行四边形的性质证明三角形ABE全等于三角形CDF，再利用三角形全等得到AE=CF及角相等，进而证明AE∥CF。

解法2：本章主要讲平行四边形，平行四边形有对边平行且相等的性质，故连接AF、CE、AC，利用平行四边形ABCD得到的条件，证明四边形AECF是平行四边形，从而得到AE∥CF，AE=CF。

通过多角度寻求解决问题的办法，拓宽学生的思维，帮助学生总结做题方法。

综上所述，教师可通过科学设置问题发散点，创设良好的学习情境，引导学生自主探究，构建知识体系，鼓励一题多解等方式培养学生的数学发散思维能力。

【参考文献】

[1] 王涛 . 初中数学课堂中学生发散性思维能力的培养[J] .新课程导学，2018(11)：96.

[2] 毕建华 . 初中数学教学中学生发散性思维能力培养策略探究[J] . 新课程 · 中学，2018(04)：180.

[3]吴利辉.初中数学发散思维能力的培养策略分析[J].教育界,2020(25):44-45.