六轴机械臂集成支架的拓扑优化设计

六轴机械臂集成支架的拓扑优化设计

曾军亮

（华人运通（江苏）技术有限公司上海分公司，上海，201114）

摘要：以一阶模态不低于55Hz为约束条件，以体积最小为优化目标，建立了拓扑优化的数学模型。建立了六轴机械臂集成系统的有限元模型，进行了六轴机械臂集成支架的优化设计，得到了最优构型。制定了六轴机械臂集成支架的工程方案，工程方案的质量为0.65kg，较优化前质量减少了62.4%，满足了轻量化设计要求。进行了采用工程方案的六轴机械臂集成系统的模态分析验证，一阶模态为57.7Hz，满足了设计要求，验证了拓扑优化结果的准确性。

关键词：拓扑优化;有限元;轻量化;模态分析;结构设计

Topology optimization design of integrated bracket for six-axis robot arm

Zeng junliang

(Shanghai Branch of Human Horizons (Jiangsu) Technology Co., Ltd. Shanghai, 201114)

Abstract: The mathematical model of topology optimization is established with the first-order modal not less than 55Hz as the constraint condition and the minimum volume as the optimization objective. The finite element model of integrated system for six-axis robot arm is established, the optimized design of integrated bracket for six-axis robot arm is carried out, and the optimized configuration is obtained. The engineering proposal of integrated bracket for six-axis robot arm is determined, the mass of engineering proposal is 0.65kg, which is reduced by 62.4% compared with that before optimization, meets the requirement of lightweight design. The modal analysis of the integrated system for six-axis robot arm with engineering proposal is carried out. The first-order mode is 57.7Hz, which meets the design requirement and verifies the accuracy of the topology optimization result.

Key words: topology optimization; finite element; lightweight; modal analysis; structural design

0 引言

汽车轻量化是提高纯电动汽车续航里程的有效手段，开发镁合金材质零部件是实现汽车轻量化的有效途径之一[1]。在传统的车身设计阶段，往往依靠工程师的经验或类比进行车身零件的初始设计，这样很难得到最优的零件设计方案[2]。拓扑优化设计可以在满足工程结构的位移、体积、应力和柔度等约束条件下，获得材料的最佳分布[3-4]，有效降低材料密度，实现轻量化[5-6]。

本文开发一款压铸工艺镁合金材质的六轴机械臂集成支架，采用变密度法的结构拓扑优化方法对其进行轻量化设计，并对六轴机械臂集成系统进行模态分析，验证拓扑优化结果的准确性。

1 模态分析理论

模态是结构系统的固有振动特性，每一个模态具有特定的固有频率、阻尼比和模态振型[7]。模态分析是结构动态设计及设备故障诊断的重要方法，是系统辨别方法在工程振动领域中的应用[8]。单自由度振动系统的运动微分方程可表示为：

  (1)

式(1)中：为系统质量矩阵；为系统阻尼矩阵；为系统刚度矩阵；为系统激振力；、、分别为系统的位移、速度、加速度。当为0，且不考虑阻尼作用的情况下，即为0，得到不存在阻尼结构的自由振动方程，可表示为：

  (2)

式(2)的解为：

  (3)

式(3)中：为振幅；为系统第阶模态的固有频率；为时间变量；为初相位角。模态分析就是求解公式(3)的特征值，即求。

六轴机械臂集成系统为车内悬挂物，在车辆行驶过程中，由于路面和电机的振动激励，会引起悬挂物的振动，从而导致悬挂物的疲劳损坏。为避免这一现象，要求悬挂物的一阶模态不低于55Hz。

2拓扑优化的数学模型

结构拓扑优化是一种根据给定的负载情况、约束条件和性能指标，在给定的区域内对材料分布进行优化的数学方法[9-10]。连续体拓扑优化方法主要有均匀化方法、变密度法、渐进结构优化法、水平集方法等[11-12]。本文研究对象为连续体结构，采用变密度法对六轴机械臂集成支架进行拓扑优化设计。设计变量为单元密度，从0到1连续变化；目标函数为结构的体积，要求六轴机械臂集成支架体积最小；约束条件为六轴机械臂集成系统的一阶模态不低于55Hz。六轴机械臂集成支架的拓扑优化数学模型为：

   (4)

式(4)中：为第个单元的单元密度，取值为之间的连续值；为优化区域内单元密度组成的向量；为模态阶数；为设计变量个数；为第阶模态函数；为体积函数。

3 六轴机械臂集成支架的拓扑优化

3.1 拓扑优化设计空间和流程

根据周边零件的空间限制和安装点位置，制定六轴机械臂集成支架的初始设计空间，如图1所示，其中CCB安装点和六轴机械臂安装点位置区域为不可优化空间。镁合金压铸件质量轻，具有良好的铸造性和尺寸稳定性，易加工，废品率低；具有良好的阻尼系数，减振量大于铝合金和铸铁。基于以上优点，六轴机械臂集成支架选用压铸工艺镁合金材质，材料牌号为AM50，材料参数如表1所示，其初始设计空间的质量为1.73kg。划分六轴机械臂集成支架六面体网格，建立六轴机械臂集成系统的有限元模型，如图2所示。设置约束条件和目标函数，拓扑优化的流程如图3所示。

图1 六轴机械臂集成支架的初始设计空间

表1 AM50材料参数

图2 六轴机械臂集成系统有限元模型

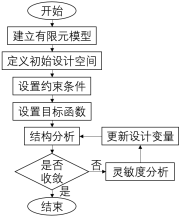
图3 拓扑优化流程图

3.2 拓扑优化结果

利用OptiStruct求解器进行求解，经过26次迭代，得到六轴机械臂集成支架的拓扑优化结果，如图4所示。深色区域为高密度单元区，主要分布在安装孔处，浅色区域为低密度单元区。根据拓扑优化结果在高密度单元处增加材料，在低密度单元处去除材料，得到的拓扑优化最优构型如图5所示，为工程方案的设计提供了参考。

图4 拓扑优化结果

图5 拓扑优化最优构型

4 工程方案及模态分析验证

根据拓扑优化主路径，结合镁合金压铸工艺和结构合理性，制定了六轴机械臂集成支架的工程方案，为了提升支架强度，在适当区域增加角筋等特征，如图6所示。工程方案的质量为0.65kg，较优化前减重比为62.4%，如表2所示，满足轻量化设计要求。

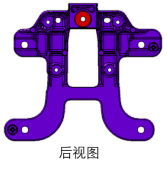
图6 六轴机械臂集成支架的工程方案

表2 六轴机械臂集成支架的重量

5 模态分析验证

划分工程方案的有限元网格，建立采用工程方案的六轴机械臂集成系统的有限元模型，设置模态分析工况的边界条件，并进行模态分析。结果显示集成系统的一阶模态为57.7Hz，如图7所示，满足汽车悬挂物的一阶模态大于55Hz的设计要求，验证了拓扑优化结果的准确性。

图7 六轴机械臂集成系统的一阶模态

6 结论

（1）建立了六轴机械臂集成支架的拓扑优化数学模型，建立了六轴机械臂集成支架的初始设计空间和拓扑优化流程图，采用变密度法进行了拓扑优化设计。

（2）根据拓扑优化结果，得到了合理的材料空间分布，提高了材料的利用率，制定了六轴机械臂集成支架的工程方案。六轴机械臂集成支架工程方案的质量为0.65kg，优化前质量为1.73kg，较优化前质量减少了62.4%，满足了轻量化设计要求。

（3）对六轴机械臂集成系统进行了模态分析，一阶模态为57.7Hz，满足了车内悬挂物的一阶模态不低于55Hz的设计要求，验证了拓扑优化结果的准确性。

参考文献

［1］徐中明，徐小飞，万鑫铭，等．铝合金保险杠防撞梁结构优化设计［J］．机械工程学报，2013，49(8) : 136－142．

［2］聂昕，黄鹏冲，陈涛，等．基于耐撞性拓扑优化的汽车关键安全件设计［J］．中国机械工程，2013，24(23) : 3260－3265．             

［3］林丹益．一种汽车发动机支架拓扑优化设计［J］．机械设计与研究，2018，34(3) : 179－181．

［4］杨宁，薛慧鹏，田海洋，等．汽车真空泵支架结构拓扑优化设计［J］．机械设计与制造，2015(8) : 186－188．

［5］王冠，周佳，刘志文，等．铝合金汽车前碰撞横梁的轻量化设计和碰撞性能分析［J］．中国有色金属学报，2012，22(1) : 90－98．

［6］韩明轩，张洪信，赵清海，等．碰撞载荷工况下某城市客车车架拓扑优化设计［J］．现代制造工程，2021(10) : 91－95．

［7］陈瑞文，尹湘云，李刚，等．考虑模态因素的齿轨动车车体地板梁的结构拓扑优化［J］．机械强度，2022，44(5) : 1141－1147．

［8］王镇江，何造，林广谊，等．基于模态分析的汽车塑料保险杠拓扑优化［J］．塑料，2017，46(5) : 9－12．

［9］尹辉俊，曹稚英，张婷婷．基于拓扑优化法的副车架概念设计［J］．机械设计与研究，2018，34(3) : 175－178．

［10］许康，廖文俊．基于拓扑优化重型自卸车后桥结构优化分析［J］．机械设计与制造，2019(7) : 73－77．

［11］马超，鹿鹏程，邱娜，等．基于强度拓扑优化的乘用车轮毂轻量化设计［J］．机械设计与研究，2022，38(5) : 122－125．

［12］徐晓，王二冬，夏琴香，等．基于变密度法的级进模模具结构拓扑优化设计［J］．机械设计与制造，2018(4) : 90－93．

7作者简介

作者简介：曾军亮，1987年11月，男，华人运通（江苏）技术有限公司上海分公司，汉，江西鹰潭，硕士研究生，工程师，主要研究方向：车身和底盘结构设计，整车安全性能集成开发，整车碰撞安全仿真和试验；机械工程与自动化、15870055950、上海市闵行区浦江镇江汉路200弄滨浦新苑三村53栋202室，201114，527392780@qq.com。

曾军亮，1987年11月，男，中南林业科技大学，硕士研究生，工程师，主要研究方向：车身和底盘结构设计，整车安全性能集成开发，整车碰撞安全仿真和试验

联系方式：曾军亮，15870055950，527392780@qq.com，上海市闵行区浦江镇江汉路200弄滨浦新苑三村53栋202室，201114