重力式挡土墙稳定性与地基承载力研究

重力式挡土墙稳定性与地基承载力研究

范少勇,刘航

航天规划设计集团有限公司

摘要：经过深入研究，我们发现，重力式挡土墙的抗倾覆稳定性与地基承载力之间存在着一种相互独立的关系，但是，由于仅仅考虑墙趾取距，而忽略了地基反力对倾覆的不利影响，因此，为了更好地评估这种结构的抗倾覆能力，必须综合考虑地基反力、抗倾覆稳定性、抗倾覆能力、抗倾覆能力等因素，以确保其安全可靠。导致力矩平衡方程无法得到满足。建议采用力学原理和相关方法，以确保重力式挡土墙的抗倾覆稳定性，以确保其安全可靠性。

关键词：重力式挡土墙；抗倾覆；稳定性；地基承载力；关联计算

引言

随着城市化的不断推进，地下空间的开发利用也日益增多。然而，由于地下空间容易受到水、热等自然因素的侵蚀，因此，在建设过程中必须采取有效的措施来保护和防治。其中，重力式挡土墙是一种非常有效的防渗技术，它具有施工简便、成本低廉、抗压能力强、可持续性好等优点，因此得到了广泛的应用。本文旨在深入研究重力式挡土墙工程中的挑战，并从结构和地基承载力的角度，提出有效的解决方案。

一、承载力规范要求

《公路路基设计规范》（JTGD30一2015）明确指出，重力式挡土墙的稳定性应当单独进行，而地基的承载力则应该与之相结合，以确保其稳定性。然而，该规范却忽略了墙趾处的力学特性，即墙趾处的力臂中心，而且也忽略了地基反力的影响，从而使得抗倾覆验算无法达到力矩平衡的要求。采用这种计算方法，由于地基具有完全的刚度，因此所有的地基反力都会聚焦在墙趾上，而且墙趾之间的间隔也会被设定为零。无论从何种视角来看，采用重力式挡土墙的抗倾覆计算方法显得过于简单，因为根据地基的承载力和变形特性，其转动中心会发生变化，而不会固定在墙趾上。因此，在建筑边坡和铁路支护结构的设计规范中，虽然它们的表达形式有所差异，但它们均把墙趾作为力矩的传递中心。由于以墙纸为力矩中心的抗倾覆验算方法，忽视了地基反力的重要性，从而使得抗倾覆安全系数的计算结果出现较大的偏差[1]。

二、规范法求解重力式挡土墙稳定性与地基承载力

图1重力式挡土墙受力简图

（一）抗倾覆稳定性计算为式（1):

K=(G·m+Ey·n)/(EX·Z)

在这个公式中，K代表抗倾覆安全系数，G代表挡土墙的自身重量，Ey代表土压的垂直作用，EX代表土压的水平作用，m代表挡土墙的中心点到墙脚的距离，n代表土压的垂直作用点到墙脚的距离，Z代表土压的垂直作用点到墙脚的距离。

（二）地基承载力计算见公式（2)：

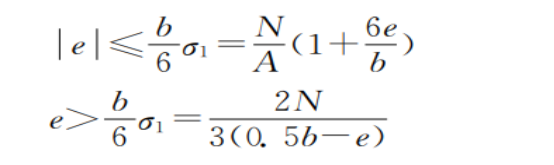
在本公式中，e代表着挡土墙的各种合力与其基础的偏心距离，N则指的是挡土墙的垂直合力，A则指的是基础的面积，b则指的是挡土墙的地基的宽度，而倾斜的基础则指的是其斜率。因此，各种规范对于重力式挡土墙的抗倾覆性能以及其地基的承载能力的评估都是完全独立的。虽然多年来一直在努力确保边坡、建筑基坑支护技术和公路路基的安全性，但是在一些特殊的工况下，重力式挡土墙的抗倾覆和抗滑移稳定性的安全系数都明显高于其他类型的挡土墙。由于构造物的抗倾覆和抗滑移能力存在差异，因此，它们的可靠性无法达到可靠性设计的最高要求，也无法达到工程可靠性的统一标准。

按照规范的抗倾覆验算公式，当安全系数K=1时，挡土墙会受到自身重量和土压力的影响，并保持平衡。但是，为了确保力的平衡，我们必须假设基底反力为零或者地基反力可以集中到墙趾A处，而不是假设岩土体具有绝对的刚性，以此来减少规范公式的误差[2]。

当不考虑土压力作用时，抗倾覆验算的竖向力的取值不能精确到墙趾。由于墙趾处的力学特性最强，因此其受力也会最大，而墙踵处的变形也会随着土压力的不断加大而不断减少，从而使墙踵与基础之间的联系越来越紧密，即使到了地基的破坏，墙趾到墙踵的距离也会被一段较短的时间内的土压力所抵消，从而使墙踵与墙趾之间的联系越来越紧密。不会聚焦在墙趾A上。重力式挡土墙的力臂取值可能会过大，但是倾覆力矩的取距可以忽略不计，因为它们可以被精确地计算出来，而且不受地基反力的影响。因此，正确选取倾覆力矩的取距中心，将直接影响到计算结果的准确性。

三、关联计算重力式挡土墙抗倾覆稳定性

通过关联计算，可以有效地将重力式挡土墙的抗倾覆验算和地基承载力计算结合在一起。这种方法的基础原理是：地基反力的力矩被设定为零，因此地基反力的合力点必定位于取距点。因此，在进行重力式挡土墙的抗倾覆验算时，应当根据地基反力的合力点取距，以确保其具有足够的准确性和可靠性。通过对比两个不同的临界状态，我们发现当没有外部压力时，挡土墙的抗倾覆能力会受到地基反力的影响，因此它的合力点会发生改变，并且它们会保持同一条垂直线。随着土压力的增加，重力式挡土墙的墙踵将会超越地基，导致墙趾处的承载力达到最高，同时，基底应力的合力中心与墙趾之间的距离也将被拉长，从而形成一个更大的垂直力臂。在这样的情况下，挡土墙的抗倾覆能力将达到极限，而该力矩将成为挡土墙的最大抗倾覆力矩，因此，我们可以利用这一结论，估算出不同土压力条件下的挡土墙的安全系数。采用程序化计算技术，我们可以精准测量挡土墙的地基承载能力，并依此来评估它的抗倾覆性能，从而获取基底的应力分布信息。重力式挡土墙的竖向抗倾覆能力是由其结构特性决定的，它能够抵御外力的影响，并且能够抵御地面的冲击。为了更好地验算这种结构的稳定性，我们需要考虑它的应力分布，并且要求它能够承受自身的重量、土压力和地面的反力。无论采用哪种受力状态，都可以用来评估重力式挡土墙在特定工况下的地基承载力和抗倾覆能力。当主动土压力达到极限值，地基承载力也会受到影响，这时才能确定抗倾覆安全系数，具体参见图2。

图2重力式挡土墙在极限荷载下受力

当处于极限状态时，基底反力的合力中心O点与墙趾A点最接近，而当处于未达到极限状态时，合力P则位于O点的右侧，因此，在临界条件下，重力式挡土墙的抗倾覆性能可以通过式（3）来计算：

m1和n1是用来描述挡土墙的自重力和竖向土压力的两个不同的参数，它们的值都与公式（1）完全一致.

经过比较，我们发现，当处于极端条件时，重力式挡土墙的安全性明显低于式（1）。通过力臂计算，我们发现抗倾覆安全系数显著高于滑移安全系数，这是实践证明的重要原因。这种方法使得我们能够更好地应对各种情况，并且符合规范规定[3]。

结语：在规范的框架下，重力式挡土墙的地基承载力和抗倾覆稳定性被单独考虑，而未能将它们结合在一起，虽然这两项指标都符合规范的要求。然而，在实际应用中，这种做法却忽视了地基反力的影响，从而使得规范的抗倾覆验算结果出现偏差。因此，必须采取措施，加强地基反力的考量，以确保重力式挡土墙的抗倾覆能力达到最佳状态，从而保证其安全可靠的使用。

参考文献

[1]曾革,周志刚.公路挡土墙抗倾覆稳定性设计方法[J].中南大学学报(自然科学版).2009(04):136.

[2]吴晓枫.土墙抗倾覆稳定性及地基承载力验算探讨[J].路基工程.2008(03):11.

[3]袁健,黄太华.挡土墙截面设计直接计算方法[J].岩土工程技术.2007(02):19.

范少勇 （1991.09）汉族，男，河北邯郸，硕士，初级职称，研究方向结构工程