双室箱梁剪力滞效应的分析

双室箱梁剪力滞效应的分析

杨俊

(重庆交通大学 土木工程学院，重庆  400074)

摘要：针对一典型的双室箱梁简支梁，根据板壳的三维数值方法和本文的解析解法，研究了均布荷载和集中力的剪力滞分布规律。本文提出的剪力滞翘曲位移模型能够反映各悬臂板之间剪力滞的差异。解析解与有限元数值解吻合良好。双室箱梁腹板顶部和底部的剪力滞效应与边腹板的剪力滞效应不同，中腹板顶部和底部的应力比边腹板的应力小。

关键词：双室箱梁；剪力滞；变分原理；有限元分析

1 介绍

本文以单箱双室梁[1]为研究对象，考虑各翼缘板之间剪力滞翘曲的差异，结合整个截面的轴力平衡条件，定义了新的适用于箱梁各翼缘板的剪力滞翘曲位移函数。基于变分原理，建立了考虑剪力滞的单箱双室梁平衡控制微分方程。针对典型的单箱双室简支梁，根据板壳三维数值计算方法和本文的解析解方法，研究了均布荷载和集中力的剪力滞分布规律。

2 双室箱梁翘曲位移函数的选择

横截面的纵向位移函数如下所示。

                     （1）

式中=箱梁的垂直位移（挠度），=箱梁转角处，=横截面任意点的纵向位移，=剪力滞的广义位移，=剪力滞的翘曲位移函数。根据箱梁截面构造，f(y)可表示为：

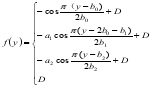
  （2）

式中，D是满足整个截面轴向力平衡的附加轴向位移，根据弯曲构件的轴向力必须等于零，即因此，D的表达式如下。

（3）

其中A=箱梁横截面面积，A1=顶板面积，A2=底板面积，A3=两侧悬臂板面积，和是反映不同法兰盘之间翘曲差异的系数，表达式见下文。

3 微分方程及其解

3.1弯曲梁体的总势能

当确定翘曲位移函数时，可根据截面的纵向位移，获得截面的弹性应变[2]

    （4）

考虑弯矩作用在梁体上，考虑应变能和势能力的总势能表达式如下所示。

（5）

式中，E=杨氏模量，G=剪切模量，Q（x）=表示剪力，M（x）=弯矩，Iu=翼缘板的惯性矩，I是整个截面的惯性矩，Iyu=翼缘板惯性矩的乘积，Au=翼缘板的惯性矩，其表达式为。

3.2和的计算

假设简支梁的跨度为l，其挠度曲线近似为根据方程式（1）

内顶板的任意横截面具有沿X轴的轴向位移。

  （6）

其中是平面截面假设中垂直弯曲的均匀位移，是剪力滞的广义位移。

内部顶板采用最小势能原（7）

考虑到能够得到，          （8）

与内顶板类似，悬臂板和底板的剪力滞位移也可以得到。

悬臂板（9）

底板    （10）

如果是一个基准，可以建立以下比例。

（11）（12）

研究公式（11）和（12）可以看出更大，换言之，翘曲位移基本上与宽度的平方成正比，也与法兰盘和中性轴之间的距离成正比。根据单室箱梁的研究，使得能满足一般跨径箱梁计算精度的要求。

3.3建立了梁段单元的剪力滞微分方程

已知剪力滞的位移函数，应用梁段的最小能量原理，可以得到以下控制微分方程和边界条件，根据虎克定律，得到考虑剪力滞效应的横截面应力公式。

（13）

4 简支单箱双室梁的解析解

结合简支梁的荷载和边界条件，利用方程（13）得到剪力滞效应的纵向应力表达式。当集中荷载的荷载P作用于跨中截面时，得到横截面的法向应力。

（14）

相应的剪力滞系数如下所示。

（15）

同样，根据荷载和边界条件，可以得到均布荷载q作用下跨中截面的法向应力。

（16）

剪力滞系数如下所示。

（17）

5 实例分析

5.1基本信息

以跨度为10m的简单箱梁为例,材料的杨氏模量为E=3.45×105Mpa，泊松比为=0.375。作用在模型上的荷载有两种形式，集中荷载P=1×105N作用于跨中截面，均布荷载q=2×104N/m作用在所有横截面上。使用shell63单元的ANSYS有限元建立了空间板壳的有限元数值模型。

5.2穿过中间截面的剪力滞效应

利用本文解析解的数值解和ANSYS板壳，单箱梁1/2和1/4截面的剪切系数如图1和图2所示。

（a）1/2节（b）1/4节

图1.集中力作用下剪力滞系数的分布

（a）1/2节（b）1/4节

图2.均布荷载下剪力滞系数的分布

从图1和图2可以看出，解析解与有限元结果非常吻合。两种工况下的计算结果表明，虽然梁体承受对称的竖向弯曲荷载，但边腹板应力与中腹板在顶部和底部存在一定的差异，边腹板应力均大于中腹板在顶部和底部的应力，且两者的最大剪力滞为12%。这表明单箱双室梁在均匀弯曲时的剪力滞系数在各板之间是不同的。

5.3剪力滞系数沿跨度变化

为了进一步分析腹板和边腹板在顶板、底板中剪力滞系数的变化，选择截面顶板和底板1、2、3和4点剪力滞系数的分布，如图3所示。

集中力（x /米）均布载荷（x /米）

图3.剪力滞系数沿跨度变化

可以看出，双室箱梁简支梁在集中荷载和均布荷载作用下，顶板边腹板1点的剪力滞系数大于中间腹板2点的剪力滞系数。同样，底板边缘腹板3点的剪力滞系数大于中间腹板4点的剪力滞系数。两部分之间的差异是L/4部分，最大差异接近12%。

6 结论

主要结论如下。

（1）结果表明，本文位移模式的剪力滞翘曲能反映出各翼板间剪力滞翘曲的差异，并与分析结果进行了比较与有限元结果吻合较好的解。结果表明，本文的解析解对集中荷载和均布荷载作用下的单箱双室简支梁具有较好的精度

。

（2）虽然它是一种均匀的垂直对称弯曲力状态，但各板之间的剪力滞系数不同。

（3）本文提出的解析解方法具有通用性，可用于多室箱梁剪力滞效应的分析。

参考文献

[1]郭建清,方志忠,郑志忠.箱梁设计理论[M].中国交通出版社.北京(2008).