三角形中2倍角解题方法的探索

三角形中2倍角解题方法的探索

马贵军

哈尔滨第六十九中学校，哈尔滨   150010

三角形中的2倍角是指三角形中，存在其中的一个角是另一个角的2倍，通过角的2倍关系，通常通过作恰当辅助线来导角等，这样可以得出等腰三角形、角分线、全等、相似等，在应用上占有重要位置。解题常用法：

（1）<等腰法>  ①以二倍角为外角构造等腰三角形；②以二倍角为底角构造等腰三角形；

（2）<角分线法>作二倍角的角分线；（3）<对称法>小角或大角为对称角；

（4）<构造法> 以三个角分为2α，90°-α，90°-α，或90°-2α，45°+α，45°+α，构造等腰三角形；

探索1：邻角2倍型；

1. 已知：图1-1，△ABC , ∠ACB=2∠ABC ,

求证：（1）AB<2AC ；（2）AB2=AC2+AC·BC.

(1). <法1>图1-1，<等腰法> AC=CD, ∠B=∠D, AB=AD,AC+CD>AD,2AC>AB;

<法2>图1-2，<角分线法> ∠BCE=∠ACE=∠B,△ACE∽△ABC, AC:AB=EC:BC,

BC<2EC,EC:BC>EC:2EC， EC：BC>2, AC:AB>2 ,AB<2AC ;

(2) <法1>图1-2，<角分线法>∠BCE=∠ACE=∠B,△ACE∽△ABC,AC:AB=AE:AC ,AC:AB=EC:BC,

AC2=AB·AE=AB(AB-BE) =AB2-AB·BE=AB2-AC·BC,即AB2=AC2+AC·BC.

<法2>图1-3，<等腰法> BC=CF, ∠ABC=∠CBF=∠F,△ABC∽△AFB,                 AB2=AC2+AC·BC.

应用1.已知：图2-1，△ABC,∠ACB=2∠ABC,AD为△ABC的角平分线，求证：AB=AC+CD .

<法1>图2-1，<对称法> AE=AC, △ADE≌△ADC,DE=DC,∠B=∠EDB=∠C, BE=ED=DC,AB=AC+CD;

<法2>图2-2，<对称法> CF=CD, △ADB≌△ADF,AB=AF,∠B=∠F=∠CDF, CF=CD,AB=AC+CD;

应用2.  已知：图3-1，△ABC,∠ACB=2∠ABC,AD为△ABC的高线，求证：BD=AC+CD .

<法1>图3-2，<对称法> DE=DC, △ADE≌△ADC,AE=AC,∠AED=∠C, ∠BAE=∠B,  BE=AE,BD=AC+CD;

<法2>如图3-3，<对称法> DF=DB, △ADB≌△ADF,AB=AF,∠B=∠F=∠CAF, CA=CF,AB=AC+CD;

探索2：一个内角被分成的一个角存在的2倍角型；这种情况，有一下三种情况，如图4-1,4-2,4-3 ；

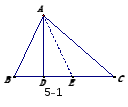
应用1：已知：如图5-1，△ABC,AD⊥BC,∠CAD=2∠BAD,若BD=3,CD=8,求AB的长；

<法><角分线法>∠BAD=∠DAE=∠EAC,<对称法>△ADB≌△ADE,BD=DE=3,

EC=5,角分线AE,AD:AC=DE:EC=3:5,勾股得AC=10,AD=6,AB=    ; 

应用2：已知：如图6-1，△ABC中，AD⊥BC,∠C=2∠BAD,求证：CA=CB.

<法1>如图6-1，<构造法>令∠BAD=α,∠C=2α，AD⊥BC,∠B=90°-α，

∠BAC=90°-α， 构造等腰△ABC, ∠B=∠BAC,CA=CB;

<法2>如图6-2，<角分线法>∠BCE=∠ACE=∠BAD,∠ADC=∠AEF=90°,△ACE≌△BCE,CA=CB;

探索3：两个内角分别被分成得一个角存在的2倍角；

这种情况，有一下两种情况，如图7-1,7-2 ；

应用1：. 如图7-1，在△ABC中，D是BC上一点，

连接AD,AD=AC,过点C作CE⊥AB于点E,交AD于

点F,且∠DAC=2∠ACE,若AE=1，BD=3，求DF的长。

<法><角分线法> ∠DAR=∠CAR=∠ACE=α,<构造法>∠BCA=∠BAC=90°-α, ∠B=2α,

BA=BC,△ACE≌△CAR ,AE=CR=DR=1,BR=BE=4，AR=CE=3，tan∠FDC=3,

tan∠FCD= ,设DT=m,FT=3m,TC=m,DC=m=2,m= ,FD=;

应用2. 已知: 如图9-1，△ABC中,∠BAC=90°,AB=AC,点D、E

分别为AC、AB上的点，∠ABD=2∠BCE,AE=2,AD=3, 求BC的长；

<法><构造法>  AF=AD, △ACF≌△ABD,

AF=AD=3,∠ACF=∠ABD=2∠α,∠FEC=∠FCE=45°+α,

FE=FC=5,勾股AC=4,BC= ;

通过2倍角的探索与应用，会让大家利用上述2倍角的恰当转化，熟练辅助线的做法，构造等腰三角形或全等三角形，然后利用它们的相关性质求解。这个探索过程更能大家深深体会到数学确实是训练思维的体操，感受到数学学习的奥秘，乐在其中。