课堂教学过程中实施整体教学思想的几点思考

课堂教学过程中实施整体教学思想的几点思考

王斌杰

山东省青岛第七中学 

摘要：整体性的教学设计就是把每一个知识点都放到完整的单元知识结构中去理解，促使学生建立新旧知识之间的关联，把握知识结构整体，从而通过已学习的知识和方法解决新知识和新问题。

    关键词：初中数学；整体教学思想；课堂教学；

引言：整体教学设计主要分为两个方面：一方面是单元教学设计中要有整体的思想，比如初中学段函数的学习有一次函数、二次函数，在学习一次函数的起始课时就应该涉及到反比例函数和二次函数；另一方面在课堂授课阶段对所探究的知识点要有一个整体的感知，比如学习平行线的判定时，两条平行线被第三条直线所截，应该引导学生进行全面的猜想：通过同位角、内错角和同旁内角的数量关系来判断两直线的位置关系。

目前课堂教学中存在一些问题，比如在讲一元一次方程的概念时只讲一元一次方程的概念没有形成整体感知，因为教材是把知识点以碎片化的形式呈现给老师和学生的。如果教师在教授知识的过程中仍以碎片化的思维或形式把知识传授给学生，那么学生在形成知识过程中，知识和思维必然是碎片化的。在教学过程中为实施整体的教学思想，我尝试了以下的做法。

一、单元设计要有整体的思想

对于每一学段的知识板块要有一个整体的认知和设计。比如对于方程或函数或几何图形等同一类知识但是属于不同单元板块的设计分成两个阶段：第一阶段通过学习探究不仅获得相应的知识，找到解决问题相应的思路和方法，构建起知识体系。第二阶段学习同一类知识时，运用第一阶段研究的思路和方法，进一步探索新知识。下面以等腰三角形性质和直角三角形三边关系的学习为例进行教学设计。

第一学习等腰三角形的性质时，首先了解等腰三角形的基本概念：顶点、腰、底边、底角等，然后重点研究等腰三角形的性质：是从以下的角度进行研究的：

1、两底角相等；2、两腰相等；3、三线合一；4、轴对称性

   同学们通过观察、测量、折叠或者逻辑推理等方法在教师的引导下得到等腰三三角形的相关性质。学生掌握相关的知识点以及它们的探究方式和方法，也为后面研究直角三角形、特殊四边形的性质的学习做好准备。

   2、下面是直角三角形三边关系的探究过程部分教学设计：

师：同学们前面我们一起认识了三角形，从角、边、特殊线段（角平分线、中线、高线）、轴对称性四方面研究了一般三角形和特殊三角形（等腰三角形、等边三角形）的一些性质。请你填表回忆相关内容。

设计意图：学生们通过自主复习，不经可以回忆相关的知识点：边角中线高线角平分线的相关的性质，进一步可以将知识点迁移到直角三角形具备的怎样的性质，以及研究的方法

师：我们已经对等腰三角形的性质进行了研究，但对直角三角形只进行了角的研究，那么直角三角形的三边之间会有什么数量关系呢？特殊三角形中的特殊线段还会有其他性质吗？

  整体教学设计的意义就在于改变点状、孤立的教学方式，使认知整体化。减轻学生的记忆负担，使学生对知识进行内在联系的沟通；有利于学生形成整体的思维方式，用整体的眼光去发现问题，培养学习能力。也有利于学生形成主动发展的人生态度。

二、课堂教学设计从思维策略到具体方法进行设计

比如说平面直角坐标系，整体感知的时候，从一维的数轴到二维的平面，到三维的极坐标。

提出问题：

如图：公园、家、超市在一条东西走向的直线上，公园距家4千米，超市距家3千米，请你以家为参照物，表示出公园和超市的位置。

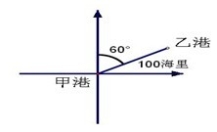超市：______千米；公园：_____ 千米

图中A点在甲港的_____偏_____方向上，距离甲港_____海里。

归纳：航海中知道和便可确定物体的位置。

归纳：直线上一个点的位置由两个数据来确定

进一步探究如何建立平面直角坐标系

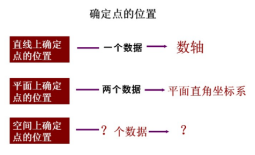设计意图：让学生体会平面直角坐标系概念的生成过程，体会相比于其他方法的简明学生自己体会点的位置确定更加简明，引出坐标等相关概念

本节课小结：

设计意图：类比数轴提出问题：进一步提出：直线上确定一个点的位置可借助于数轴，平面内确定一个点的位置我们可以借助于什么？通过经历平面直角坐标系的建立以及点的特点的探究，体会数形结合、分类思想的运用。在最后总结时提空间内确定一个点的位置我们可以借助于什么？为以后学习极坐标做好铺垫。

在课堂上，整体数学思想的落实是教师。摆脱了只有知识点，没有整体只见树木不见森林的教学状态，使学生摆脱了大量机械，重复性的学习，减轻了课业负担，是隐藏在知识背后的教学方法和数学思想。思维方式。得以呈现

三、课堂教学中要体现整体的教学思想

教材中知识是点状分布的，例如对方程的学习，北师大版教材分布在初一、初二到初三三个学段。教学的过程中如果不注意引导学生经历概念的形成过程，而是用演绎概念的方式直接呈现概念，忽略知识之间的联系，以及知识中内涵的丰富育人资源，那么教师教起来难，学生掌握起来更难。

比如说方程的分类单元按次分。

师：我们现在来观察这些整式方程，从未知数的角度来看有什么特点？

（1）2x-1=15      （2）x2=4       （3）(1+40%)x=140   （4） 40+5x=100     

（6）2a+b+c=8     （7）x2+9=0     （8）3x+y=10       （9）2x=6+y    （10） a3=15

学生可能有以下几种分类情况存在：

先按照所含未知数个数进行分类，按照未知数指数进行分类；

先按照未知数指数进行分类，再按照所含未知数个数进行分类。

设计意图：此问题具有一定的开放性，而且对学生来说也具有一定的挑战性。学生可以从不同角度进行分类。因为分类角度的多样性，并且分类的原则要自己确定，所以对初一的学生有难度，就要将这个任务互动起来，让学生们在交流的过程中判断自己的分类标准的合理性，锻炼语言表达能力，树立信心。

总之树立教学的整体思想，把各种要素组织成为一个融会贯通的整体；从整体上分析知识之间的内在联系，根据知识结构关系对教学行为进行系统整体策划，进行有层次的整体性设计，使教学由原来点状教学转化为整体的教学，使学生虽然身处陌生复杂的新环境，却能用综合的眼光去发现问题和解决问题。