基于时间序列预测的黄河水沙监测数据研究

基于时间序列预测的黄河水沙监测数据研究

赵梦蝶1，李欣雨1，刘增睿1指导教师：杨晶2

1.山东协和学院 计算机学院， 山东 济南250109

2.山东协和学院 基础部，山东 济南 250109

【摘要】研究黄河水沙通量的变化规律对环境治理，气候变化和人民生活具有重要的意义，根据水沙通量的公式计算出6年的水沙通量，观察水沙通量的变化曲线，直观分析其突变规律，后利用Mann-Kendall突变检验法，通过M-K统计量曲线定位出每年的水沙通量突变点位置和整个6年的突变点位置。基于水沙通量数据的时序特点，进行时间序列分析得到水沙通量的季节性和周期性规律。

【关键词】Mann-Kendall  突变检验法  时间序列分析

【中图分类号】TN248.1

一、前言

黄河是中华民族的母亲河，根据近6年该水文站水沙通量的突变性，季节性和周期性等特征，研究黄河水沙通量的变化，观察水沙通量的趋势和变化规律。

二、水沙通量的突变性、季节性和周期性规律研究

图12016-2021年水沙通量随时间的变化曲线

2.1可视化分析

（1）水沙通量每年7-9月份都会发生大幅上升，这与季节或调水调沙有关。

（2）2018年的水沙通量较2016和2017年，发生大的突变。

（3）水沙通量在每年的变化趋势不完全相同。

2.2 Mann-Kendall突变检验模型的建立与求解

Mann-Kendall突变检验的原理如下【1】：

对具有个样本量的时间序列，构造如下秩序列：

其中：秩序列是时刻数值大于时刻数值个数的累计数。在时间序列随机独立的假定下，统计量为：

,是累计数的均值和方差，在相互独立，且具有相同连续分布时，可由下式算出其中：

通过K-M检验对6年的水沙通量分别进行突变性分析，在0.05的置信度水平内，找到UF和UB曲线的交点，对应的时间点应该就是水沙通量时间序列的突变时间，得到以下结论：

① 2016年在第240天左右（八月）产生了水沙通量的突变；

② 2017年在第25天左右（一月）和第300天左右（十月）产生了突变；③ 2018年在0.05的置信度水平内未分析出突变情况；

④ 2019年、2020年、2021基本都在二、三月附近产生了水沙通量的突变。

⑤ 每年的水沙通量突变点没有很强的规律可循。

又将整个6年（即2016-2021）的水沙通量数据进行突变性分析：得到在2016-2022年整个六年中，水沙通量在第800天（2018年3月）产生突变

三、水沙通量的季节性和周期性研究

3.1 时间序列预测模型的建立与求解

本文将水沙通量天数据整合成月平均水沙通量数据，再进行预测。其次考虑到前两年的数据相对数值太小，因此只选择了后四年的数据进行预测。

利用SPSS软件的时间序列分析对后两年数据进行预测，做出时间序列图：

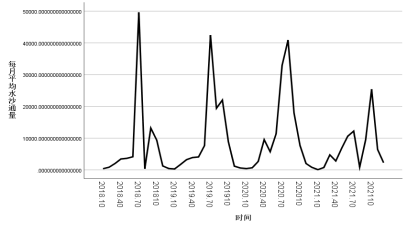
图2  2016-2022年水沙通量的时间序列图

观察曲线，初步得到水沙通量的周期性与季节性规律：

① 前两年（2016-2017年）因为水沙通量数值相对较小，所以图中的周期性和季节性不明显；

② 中间三年（2018-2020年）的周期性和季节性比较明显，每年的第三季度取得该年的水沙通量极大值；

③ 最后一年（2021年）数据的季度数据较前几年偏差大，不易观察季节性和周期性。

3.2 进行季节性分解

根据水沙通量的时间序列图可知，近几年的含沙量整体波动较平稳，故对平均含沙量采用加法分解得到季节性因素，

表1  季节性的模型描述

表2  季节性的模型描述

观察以上两表，进一步得到水沙通量的周期性与季节性变化规律：

水沙通量在第一、二、四季度的季节性因素为负，第三季度的季节性因素为正，说明水沙通量第一、二、四季度的平均量低于第三季度，且第三季度的水沙平均量高于全年平均量的11454kg/m³，这与水沙通量的时间序列图互相验证。

四、总结

本文采用了Mann-Kendall突变检验模型对近六年水沙通量的突变性进行了分析，水沙通量是随着时间变化而变化的，属于时间序列数据，因此结合本问题特点与时间序列分析的优势，本文选择时间序列分析对水沙通量的季节性和周期性进行研究。

参考文献

[1] 彭思晴.利用气溶胶垂直廓线和地面水平能见度反演气溶胶光学厚度的方法[D].云南大学,2016

[2] 韩中庚.数学建模方法及其应用，北京:高等教育出版社，2017.

论文来源：2023年“高教社杯”全国大学生数学建模竞赛

 论文来源：2023年“高教社杯”全国大学生数学建模竞赛