双通道采集卡实现高频信号频谱分析

双通道采集卡实现高频信号频谱分析

于煜

341623199404072615

摘要：根据奈奎斯特采样定理，采样频率必须大于采集信号频率的两倍才能实现信号的有效采集，基于傅里叶变换的中心对称性，实数傅里叶变化的有效频谱信息也只有半个采样频率谱宽，但傅里叶变换处理复数信号时的能得到从零到采样频率范围内全部的频谱信息。基于这一特性，文章提出了一种采用90°相位延迟方式结合双通道采集卡实现信号的复数形式采集，然后进行复数域傅里叶变换，使用两个低采样频率的采集卡成功分析出了满采样频率的频谱信息，并与高采样频率的采集卡得到的信号进行对比，两种方式分析得到的信号频谱信息高度一致，且有效减少了计算量、提升了计算速度。

关键词：复数傅里叶变换；双通道采集卡；满采样频率频谱分析

1 引言

快速傅里叶变换（FFT）在信号处理分析领域占有至关重要的地位，是目前信号频谱分析的主要手段，随后出现的小波变换、短时傅里叶变换等也只是在傅里叶的基础上进行优化。常见的傅里叶变换多用于实数域的信号分析，这种分析手段受限于奈奎斯特采样定理的限制，即采样频率必须大于信号频率的二倍才能有效的对信号进行频谱分析，称之为半采样频率频谱分析。在进行高频信号处理的过程中硬件采样频率的提升会伴随着成本的快速增加，往往采样频率增加一倍成本会增加3到4倍甚至更多，同时计算量增加，对后续的信号处理硬件要求较高。

针对固定频率的高频信号可以通过降低采样频率的形式采集，然后通过复杂的算法进行反推计算该信号的频谱信息，但是针对频率不断变化的高频信号这种方法就失去了作用。另外一种解析高频信号的方式是通过混频的方式将信号的频率降低，然后再进行信号频谱信息的反向计算，这种方式往往也只适用于频率变化范围较小或者频率规律性变化的信号，在频率变化范围较大时也会出现计算错误的问题。文章针对高采样频率的成本较高、计算量大的问题，提出了一种使用双通道低带宽采集卡的方式实现了高频（零到采样频率范围）信号的采集并有效分析出了信号的频谱信息，称之为满采样频率频谱分析。

2 系统方案

在实际测量应用中信号多为模拟信号，需通过采集卡等采集设备转化为数字信号进行后续处理，如下图1所示。首先使用模拟电路将模拟信号进行分路，其中的一路通过微分电路做90°相位延迟，然后利用FPGA输出时钟和相应的控制信号驱动AD1和AD2进行同步数据采集，FPGA将相位延迟的一路作为信号的虚部，未延迟的一路作为信号的实部进行复数域FFT并将采集和处理

所用数据存储在外部SDRAM中，最后输出处理后的信号量进行后续分析与处理。

图2.1 双通道采集卡实现高频信号分析原理

该方案在原有的基础上添加一个微分电路和采集卡AD2，通过FPGA实现了一个简单的时钟同步即可实现使用两个采样频率的采集卡实现复数形式采集并进行频谱分析。该系统原理简单且易于实现，在实现高频采样和大批量生产的情况下成本更加低廉。

本质上实数域的傅里叶变换只是令信号的虚部全为零。由于实数信号的偶对称性导致傅里叶变换的结果关于中心对称，在实际分析时只能实现半采样频率频谱分析，且变换时虚部的零值全部参与计算，增加了大量的无效运算；而复数域的傅里叶变换虚部和实部分别是奇对称和偶对称，所以不会存在中心对称的现象，能够分析出零到采样频率宽度全部的频谱信号，此时虚部的数值为有效值，在计算中属于有效运算，例如傅里叶逆变换就是一种复数信号的傅里叶变换，这种变换的结果就不关于中心对称。数字信号处理中主要使用离散傅里叶变换，其变换公式如下。

傅里叶变换：

傅里叶逆变换：

首先使用MATLAB进行复数傅里叶频谱分析的仿真验证，建立一个为20MHz的信号，使用300MHz的采样频率进行采集用以模拟探测器接收到的模拟信号，对其进行傅里叶变换得到的频谱如下图2（a）所示；对该模拟信号进行微分处理，对原始信号和处理结果进行30MHz抽样采集模拟采集卡的采样频率，被微分处理过的信号作为虚部，原始信号作为实部进行复数域傅里叶变换，得到计算频谱如下图2（b）所示；

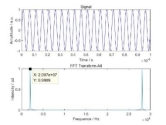
图2 复数信号傅里叶变换仿真图

根据上述仿真结果证明，该系统使用两个30MHz的采集卡同时采集数据，成功分析出了20MHz频率信号的频谱信息，与使用300MHz采集卡分析结果一致为20.07MHz，可以实现满采样频率的频谱分析。

3、实验结果

目标信号的频率为20MHz，该系统使用两个采样频率为31.25MHz采样频率的双通道采集卡AD1和AD2进行数据采集，同时将该模拟信号使用时钟同步的312.5MHz采样频率的单通道采集卡AD3采集处理。将处理结果和信号使用MATLAB读取并绘制成曲线如图3.1所示：其中使用AD3进行采集的信号的时间信号和幅频曲线如下图（a）所示，图中为了比较两种方式处理结果的异同，只显示了0-35MHz的幅频信息；使用AD1采集处理高频信号的曲线为图（b）中绿色曲线，AD2采集到的信号为图2（b）中红色曲线所示，根据两路信号进行傅里叶变换得到的幅频曲线如下图（b）中蓝色曲线所示。

图3 双通道采集卡信号及频谱曲线

如上图所示，对同一组信号使用高采样频率的单通道采集卡处理结果与双通道低采样频率的采集卡处理结果基本一致，其中可以明显的观测到双通道采集处理系统的处理结果在12MHz左右多出一个明显的小峰，经过分析得出该峰是由于微分电路的相位延迟不是准确的90°，对该现象进行验证性实验，使用信号发生器给出稳定的20MHz的正弦信号，分为两路后将其中一路信号分别作90°、120°、150°和180°延迟，仿真结果如下图所示：

由上图可知，随着相位延迟误差逐渐增大，在关于中心对称位置处出现的峰值就越大，达到180°时双峰高度达到一致，随后再次逐渐减小，达到360°时实部与虚部相等，与实数域信号的傅里叶变换结果一致。

4、结论

该双通道采集系统能有效的对满采样频率的频谱信号进行分析，在90°相位延迟准确时能实现与高带宽采样频率采集卡采集信号处理结果高度一致，且计算量远低于两倍采样频率信号的采集数据，在针对较高频率信号处理时能有效降低系统的成本。

参考文献：

陶海军,张一鸣,曾志辉.基于 AD7606 的多通道数据采集系统设计[J].工矿自动化,2013,39(12):110-113．

牛婉琳,刘磊,甄国涌,等.基于 AD7173 的多通道数据采集高速存储系统[J].中国测试,2018,44( 03):149-152．

刘喜梅,吕文韬.基于 AD7606 的树莓派多通道数据采集系统设计[J].工业仪表与自动化装置,2021(04):98-101.

郭峰.多通道动态信号采集系统研究与设计[D].中北大学,2021(06).

作者简介：于煜（1994-），男，安徽亳州人，大学专科，助理工程师，现供职于安徽首佳电力工程勘察设计有限公司，研究方向：电气工程。