奇偶数列问题多视角的解题策略

奇偶数列问题多视角的解题策略

吴秀芝

临沧市第一中学 

《高考蓝皮书—高考试题分析》（2024版）提出了对于数列的备考建议.数列问题特别突出对学生的数学思维能力的考查，所有问题的设计要始终贯穿观察、分析、归纳、类比、递推、运算、概括、猜想、证明、应用等能力的培养，既通过归纳、类比、递推等方法的应用，突出数学探究、理性思维的培养，从近几年的高考题可以看出，数列部分主要是以考查基础知识为主，同时锻炼学生的运算求解能力、逻辑思维能力.

   在新高考视角下，改变相对固化的试题形式，增强高考试题的开放性，减少死记硬背和“机械刷题”的现象。近几年高考试题中对奇偶数列问题的考查形式多样.没有固定模式，重视考查学生的观察、分析、信息整理能力，以下是对于学生在高考复习中遇到的一些类型的奇偶数列问题，在新高考视角下的解题策略的一些总结和建议.

一、高考真题呈现

【类型一】递推式分奇偶

（2021.新高考1卷）已知数列满足a1＝1，an+1＝

（1）记，写出b1，b2，并求数列{bn}的通项公式；

（2）求的前20项和．

解析：（1）因为a1＝1，an+1＝，

所以a2＝a1+1＝2，a3＝a2+2＝4，a4＝a3+1＝5，

所以b1＝a2＝2，b2＝a4＝5，

bn﹣bn﹣1＝a2n﹣a2n﹣2＝a2n﹣a2n﹣1+a2n﹣1﹣a2n﹣2＝1+2＝3，n≥2，

所以数列{bn}是以b1＝2为首项，以3为公差的等差数列，

所以bn＝2+3（n﹣1）＝3n﹣1．

另解：由题意可得a2n+1＝a2n﹣1+3，a2n+2＝a2n+3，

其中a1＝1，a2＝a1+1＝2，

于是bn＝a2n＝3（n﹣1）+2＝3n﹣1，n∈N*．

（2）由（1）可得a2n＝3n﹣1，n∈N*，

则a2n﹣1＝a2n﹣2+2＝3（n﹣1）﹣1+2＝3n﹣2，n≥2，

当n＝1时，a1＝1也适合上式，

所以a2n﹣1＝3n﹣2，n∈N*，

所以数列{an}的奇数项和偶数项分别为等差数列，

则{an}的前20项和为a1+a2+...+a20＝（a1+a3+…+a19）+（a2+a4+…+a20）＝10+×3+10×2+×3＝300．

【总结与反思】本题考查了学生的观察能力和逻辑推理能力，第二问考查了分类讨论，分组求和的基础知识，学生的做题难点主要是第一问，这类分奇偶的递推式，本题还可以把n=2k-1和n=2k分别代入，将下标换成K，建立的关系式，消去偶数项即可找到奇数项的关系.

【类型二】通项为奇偶分段的数列

（2023新课标2,18）已知{an}为等差数列，bn＝，记Sn，Tn为{an}，{bn}的前n项和，S4＝32，T3＝16．

（1）求{an}的通项公式；

（2）证明：当n＞5时，Tn＞Sn．

解析：（1）设等差数列{an}的公差为d，

Sn，Tn为{an}{bn}的前n项和，S4＝32，T3＝16，

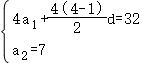则，即，解得，

故an＝5+2（n﹣1）＝2n+3；

（2）证明：由（1）可知，，

，

当n为偶数时，n＞5，

Tn＝﹣1+3+•••+2（n﹣1）﹣3+14+22+•••+4n+6

＝+＝＝，

，

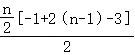当n为奇数时，n＞5，Tn＝Tn﹣1+bn＝＝，

Tn﹣Sn＝，

故原式得证．

【总结与反思】若通项按奇偶分段，只需按奇数项、偶数项分组前n项即可。考查学生的观察、分析、信息整理能力，通过对分两种情况进行讨论，考查分类讨论思想，利用做差法来比较两个数列和的大小。

二、方法梳理

【类型三】通项或递推式含的数列

已知，设，求数列的前项和．

解析：，

当为偶数时，，

当为奇数时，，

故

【总结与反思】通项公式中含有这一结构，不便于直接求和，我们先列出若干项观察规律，至少六项，两项两项求和，观察是常数列还是等差数列，求和时先求n为偶数的情形，此时恰好分整数组，再求n为奇数的情形，可通过添项或凑成偶数项，即，这样可以化简计算。

【类型四】递推式为和的关系，此为隔项成等差或隔项成等比

已知数列{an}满足：a1＝a2＝1，且，求数列{an}的通项公式；

解析：由an+2﹣an＝2n（n∈N+），

当n为奇数时，有：a3﹣a1＝21，a5﹣a3＝23，…，an﹣an﹣2＝2n﹣2，

累加得：an＝a1+（2+23+…+2n﹣2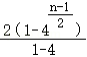）＝1+＝（2n+1）；

当n为偶数时，有：a4﹣a2＝22，a6﹣a4＝24，…，an﹣an﹣2＝2n﹣2，

累加得：an＝a2+（22+24+…+2n﹣2）＝1+＝（2n﹣1）．

又∵a1＝1＝，a2＝1＝，

∴数列{an}的通项公式为an＝．

变式：已知数列中，，成等差数列．

求的值和数列的通项公式；

解析：　因为成等差数列，，所以，

所以，得，因为，所以，

所以，得

【总结与反思】n分奇偶求通项公式，将原有的数列分为2个数列，要分清原数列中的项在新数列中为第几项，或将n转化为2k－1或2k()表示，求出通项公式．数列是一种特殊的函数，数列问题中经常出现恒成立问题，解题思路与函数的恒成立问题一致，但要注意

n的取值．

【类型五】连续两项和或积的问题（）

设数列为等比数列，且，数列满足且．

求数列和的通项公式；

解析：设的公比为，则，所以q＝2，所以an＝a2qn－2＝2n－1，

解法一：由可得，

两式相减得，

所以数列的奇数项是以为首项，2为公差的等差数列，

即是奇数时，，

那么是偶数时，，

即

解法二：由可得，

则有，

所以数列是b1－1＋＝－为首项，－1为公比的等比数列，则

即.

三、备考启示

在数学教学中，构建方法网络，总结同性通法，归纳一种题型的多样性，相对性，构建数学模型。通性通法的使用和深层次的过程，多方法、多视角、多侧面地深入理解和系统总结，才能让学生抓住数学问题的本质，将学生的知识引向深入的探究，提升学生的数学科学核心素养。在复习过程中应关注数列的函数本质，以此为切入点搭建数列与高中数学其他知识间的桥梁。理解数列与其他数学知识之间的内在逻辑联系，加强函数与方程思想，转化与化归思想、分类讨论等基本思想方法的渗透。复习过程中需重视学生重视对学生思维品质和思维过程的培养，避免机械刷题，即求解与数列有关的现实情镜时，需引导学生根据情镜抽象出数列的表达形式。如通项公式或递推关系，通过运算进行求解，最后结合实际意义作答，即经历审题、建模、反馈等系列过程，帮助学生在实践中不断提高创新能力和数学建模核心素养，体会数学的育人功能。