航空发动机管路动力学特性研究

航空发动机管路动力学特性研究

侯启航  夏芷若  王瑞阳

中国民用航空飞行学院民航安全工程学院 四川德阳 618000

摘要：管路是航空发动机的主要附件之一，包括燃油管路、滑油管路和气体管路等，是航空发动机正常运行的必备结构。由于航空发动机工作时必然产生复杂的振动载荷，这些振动载荷又通过连接部件传递到管路上，从而极易引发管路系统振动超限，诱发管路及连接件发生疲劳断裂或强度失效等故障。为了提高航空发动机管路系统在服役期间的可靠性，在设计初始阶段需要开展动力学特征研究和优化，避免与航空发动机运行时的振动频率重合而发生共振。本文以动力学理论为基础，采用仿真结合试验的方法，开展航空发动机振动激励作用下管路的模态和管路连接部位的应力变化规律研究，揭示航空发动机管路结构的振动特征，提出结构优化方案，为减少航空发动机振动对燃油管路的影响提供理论依据。

关键词：航空发动机；管路；动力学理论;仿真试验;应力变化规律

引言

输送燃油、滑油、液压油、空气等工作所需材料共同组 成航空发动机外部系统，航空发动机作为飞机动力核心，对飞机安全飞行有重要作用，也是发动机零件最多之处，外部管路是否完整将直接影响发动机的动力。

发动机管路系统具有以下特征：①零部件数量众多、结构特征多样，难以形成统一的动力学建模方法；②管路系统安装在机匣上，承受来自发动机不同区域的不同性质载荷激励，如发动机高低压转子不平衡激励、叶片气流扰动激励、燃烧脉冲激励、齿轮啮合激励、燃油泵／滑油泵输出流体脉动激励［３－４］；③发动机管路通过卡箍、支架等结构件相连，存在大量结构耦合。

目前中国发动机管路系统的设计思路依旧采取先经验设计，再型号验证，出现问题进行改进的设计方法，如图1所示。但是由于发动机管路之间大量耦合的存在以及管路之间的相互影响，造成多根管路同步修改的现象。对于管路系 统响应，以动应力为评判依据，如果测试动应力超过标准值，则修改卡箍数量、位置及管型参数，并重新进行经验设计，周而复始，延长设计研发周期。由于发动机管路系统结构的复杂性、激励的多源性、以及耦合的关联性，使得其在工作过程中极易出现由于设计不合理导致的管路系统共振，以及由于动应力过大诱发管路疲劳使得发动机系统提前失效。

早期世界航空大国对外部管路重视不够，导致发动机管路系统断裂、漏油、渗油故障频发［５－６］。 中国某型发动机在试车过程中，由管路系统共振及动应力过大等振动 问题诱发故障也较多［７－１０］， 直接影响试验进度，有时甚至影响发动机的整个研发周期。

随着航空液压系统进一步向高速、高压发展，对管路系统的总体要求不断提高，故针对管路系统动力学响应分析需求日益迫切。航空发动机外部管路作为航空发动机中各个部件之间的连接纽带，其振动特性对于航空发动机外部部件的影响是十分重要的，而又由于管路管径、形状变化复杂，没有固定的规律性，所以对于航空发动机外部管路系统的振动响应做出准确的分析是十分有必要的。本文针对这一问题，采用ANSYS有限元软件进行仿真结合试验，围绕不同的管路夹持形式，对管路固有特性及振动响应、管路的模态和管路连接部位的应力变化规律进行研究，提出结构优化方案，并对未来发动机管路系统动力学研究方向进行了展望。

图1 航空发动机管路系统设计全流程

FIG. 1 Whole process of aero engine piping system design

1 导管仿真模拟方案

航空发动机外部管路敷设较为复杂，并且管路之间具 有振动耦合。所以在解决实际问题时，应当针对管路系统整体进行典型线路分析。发动机管路构造能够决定未来的发动机机能，还会与导管卡箍等其他系统有相互影响关系。所以在设计管路结构时应当根据动力学设计，利用有限元计算仿真模拟方式获得最优管路布置方式。

1.1有限元仿真方案

1.1.1导管模型

利用ANSYS模拟软件，将SOLIDI185、SHELL181、 PIPE289 这些单位作为基础构造模型，以三种单元频率进行分析，标准要求误差不能超过0.1%。在拥有管理模型情况下，可以通过SOLIDI185实体单元构建模型，将IGES接口与模型ANSYS 衔接，将模型构建，若没有实体模型可以利用PIPE289管单元进行建模，利用管路以及截面积参数将模型构建。通过计算时间，在精度接近时，能发现建立模型单元数量较少，并且建模时间以及计算时间较短，使用较为方便。一般管路接头部位会使管套结构中所含有的管路刚度以及质量等发生变化，逐渐能够对整体产生影响，建模过程中需要注意，建模需要根据实际所需要的尺寸进行组建。

1.1.2支撑部件仿真模拟

导管常用的刚性支撑卡箍、弹性支撑卡箍、活动支撑固定、辅助支撑固定等，可以通过位移约束、弹性调整等方式建立实体单元、弹簧单元以及多点约束单元。

1.2 解析方式

在动力学基础上，能够利用公式对震动情况进行描述： cosβlchβl=1Y（ix）=Ci[cosβix-chβix+r（i sinβix-shβix） （1）

（2）

通过公式（1）可以发现：

βil=（i+ 1 2）π，i≥2

将公式带入能够得知β1l =4.752、β2l =6.481、β3l = 11.251、β4l=13.214，固有频率为：

Wi =（βil）2 √EI/pAl4     （3）

在此公式中，E的含义是弹性模量、I的含义是惯性矩、p的含义是梁材料密度，A的含义是梁截面面积，l的含义是梁的跨度，通过数值带入能够将震动幅度计算出。

1.3 仿真模拟方式

通过敲击模拟试验或者台架贴片方式获取管路振动频率，以上两种试验方式所检测结果小于等于10%，并且在实际应用中各自有优势和缺点。模拟试验方式具有较多优势，能够节省较多成本，并且测试方便，能够影响较多模态特性，影响范围较大，但是模拟会受到测试条件限制，与实际工作有一定差异。台架贴片测试能够反映导管实际情况，并能测量导管振动应力值，但是获取所花费的资金多，并且没有较大实际作用，没有办法取得模态振型。通过这种仿真模拟方式，能够得出近似于实际工作的模拟形态。

2 管路结构系统动力参数研究

能够影响管路振动特性原因主要有四种，等直线管段数据数值、弯曲管段数据数值、装配段数据数值以及流动液体数值。其中等直线管段数据数值中有包括像管壁厚度以及管壁直径和管壁跨度等方面数据，弯曲管段数据数值又涵盖了管壁弯曲情况以及弯曲角度大小，并对固定支点偏移角度和螺栓的预紧度进行分析。流动液体主要是对管内增加液体物质，需要对流体的密度、压力等数据进行计算。

2.1 等直线管段尺寸参数

将直管作为分析案例，通过有限元计算和理论公式对 比方式，将壁厚、直径以及跨度对横向震动第一阶段频率相对值影响规律进行试验。试验后发现，壁厚增加，导管基频下降，出现这种现象的原因是壁厚增加使导管刚性质量发生变化。壁厚在0.6-1.4mm 区间时导管基频变化值小于5%，所以在设计时能够达到调整壁厚共振的目的。导管直径在扩大时，导管振动频率会减慢，若导管直径在6-28mm的情况下，基本振动频率会产生较大变化，出现这种情况的原因是导管直径的大小会对导管面积产生影响，在直径扩大后，解析数以及数值解之间呈现出较大变化，在理论基础上，导管会出现不同程度的变形，然后对导管直径进行计算，能够使结果更加准确。随着导管跨度增加，基频指数数值下降，在 300-800mm跨度区间内，基频变化值较80%大，导管跨度能够对振动幅度产生较大影响。

2.2 弯曲管段尺寸参数

在研究弯导管时，可以通过计算有限元使导管弯曲半 径及角度前3阶数值产生变化，并对前3阶导管绝对值进行验算，经过计算后可以发现，弯曲角度增加后，导管各阶频率会产生较大变化，当弯曲半径为25-40mm时，导管前3阶变化频率在80%以下，弯曲角度越大，频率越大，若弯曲角度在85-145°时，固有频率变化范围不会超过13%。

2.3 装配参数分析计算

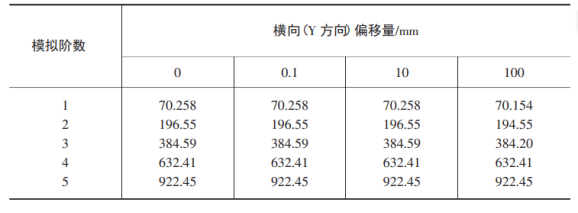
实际工程开展中，导管支架以及卡箍螺栓张力经常出 现不够的情况，通过本次模拟能够发现，固支点偏移量变化以及螺栓的紧密程度能够对导管模型产生不同程度影响，所以要具体问题具体分析。经过模式研究能够发现导管前5阶基本频率数值会随横向偏移量变化数值变化。见表1。在表1中能够发现，当偏移量变化小于10mm时，固有规律频率没有明显改变，所以，可以将安装偏移模拟情况产生影响忽略。但是，开始阶段安装出现问题则会使导管内部应力过大，从而使强度能够引起间接破坏。在胡可定理的前提下，将预紧力指固定卡箍螺栓拧紧力矩安装，通过试验研究发现，应力数值变化，会对卡箍刚度以及预紧力等产生影响。卡箍在不同螺栓预紧作用下不发生变化。

表1不同横向偏移量固有频率变化(Hz)

Table 1 Natural frequency changes with different lateral offsets (Hz)

2.4 流体介质分析计算

通常在压力的作用下，对航空发动机内部会产生一定影响，例如导管内燃油气体等介质会对导管在横向振动中造成一些影响。本文主要采用ANSYS的相关模板对航空发动机导管湿模态进行分析，并且要根据其特征选择适宜的方式。试验后要将不同种类的外径管产生数值进行计算，通过对计算数值分析可知，导管内液体在一定时间内能够形成下降的现象，并且下降频率基本能保持稳定。但通过有效的试验证明在导管中导入不同的液体会导致下降程度有所不同。本次试验主要利用气体、水、滑油、燃油四种材料进行分析，发现变化规律主要是发动机外部管路内燃油压力正常值为 10MPa，那么压力值会达到20MPa，滑油等都会出现不同程度变化，能够计算出导管内不同压力变化，若导管内液体流动速度为固定值，流速不会对管路固有频率产生影响。

3 管路金属橡胶卡箍刚度试验

航空发动机外部管路称为发动机的“心血管”，是发动 机重要组成部分之一，而对管路起着固定连接作用的卡箍， 对管路起着支承减振的重要作用。国内航空发动机管路单联 卡箍一般由箍带、金属橡胶和连接螺栓三部分组成。卡箍的 支承刚度对管路的固有特性存在巨大影响，如若安装不当， 在外界激励的条件下诱发管路共振，轻则使管路剧烈振动， 重则引起管路或卡箍的振动破坏，造成发动机故障，甚至飞 机损毁。本文通过自主设计金属橡胶卡箍线刚度和角刚度 试验测试装置，试验测量卡箍刚度。获得卡箍的支承刚度特性，并通过前文描述的有限元仿真模拟，通过一阶优化算法，优化金属橡胶等效弹性模量，达到仿真与试验结果匹配的效果，为复杂卡箍刚度的预估提供一种简单试验方法，此外也为后文工作提供基础。

3.1 金属橡胶卡箍刚度试验装置

金属橡胶卡箍通常由箍带、金属橡胶和连接螺栓三部分组成，如图2所示，首先对卡箍的方向进行定义，定义加载 力方向如图 2（b） 所示。金属橡胶与箍带通过焊接固定，如图3所示。

对于单联金属橡胶卡箍线刚度，由文献［11］结果知线刚度在ｌｘｌ0６Ｎ／ｍ数量级，即在卡箍夹持实心管上施加 100Ｎ的作用力，大致变形ｌｘ10-６ｍ，变形微小，因此采用 千分表测量，试验过程中测量位移，可以满足试验精度。本 文试验测试装置采用螺纹配合装置进行位移加载，内部通 过弹簧支承控制加载卸载的进给，通过弹簧放大手轮的前进及回退距离，方便控制，防止加载、卸载过程中间隙的存在， 测量装置各部分示意图如图4（ａ）所示。试验过程中通过旋转加载手轮，加载轴缓慢前进或后退，压缩或拉伸力传 感器，最终将位移施加在卡箍上，通过选择进给机构内的合适刚度的弹簧，保证在加载和卸载过程中方便控制，并且防 止加载和卸载过程中的空程问题的存在。力传感器如图4（ａ）中所示，力传感器通过Ｍ８的螺栓与两端结构相连，力传感器外接显示屏可以实时显示拉压力数值的大小。力传感器左端螺栓可以旋转，能保证将旋转转换为直线位移，千分表通过磁座固定，测量卡箍处的夹具位移，即卡箍夹持实心管的相应位移，采用实心管进行测量，使试验测试结果尽可能反应卡箍自身的刚度特性。对于单联金属橡胶卡箍角刚度测试装置，整体角刚度测试装置的三维模型及实际照片如图4（ｂ）所示，各部分位置布局如图所示，采用涡轮蜗杆结构，装置左端为操作手轮，由于蜗轮蜗杆传动比 为１：４，模数为1.5，所以在测试过程中能够十分容易的进行手动控制，进而施加扭矩，测试过程中通过旋转手轮进行施加载荷在卡箍上，测试过程中控制角度的增加，角度每增加１°，记录一次扭矩数值，角度传感器采用北微倾角传 感器ＢＷＬ326，分辨率为0.01°，测量范围为±90°，而在试验中，测量航空发动机外部管路卡箍时，转角一般为±10°以内，所选用的角度传感器完全满足试验要求，角刚度试验装置传感器具体参数见表2所示。

角度传感器通过３Ｍ胶带粘贴在下面底座位置，与加 载轴旋转保持同步。扭矩传感器两侧通过12个Ｍ４螺栓连接，保证测量时紧固无缝隙，通过数字显示屏，显示实时扭矩数值，右侧连接选用￥58实心钢柱，以防测试过程产生变形，卡箍夹持在实心的钢柱上。力矩由力矩扳手进行控制。此外，卡箍通过螺栓拧紧在立柱上，考虑到装配空间，可通过套筒等调节拧紧力矩。装置多部分可以移动，能够保证测试过程中位置的可调与灵活性，如左侧蜗轮蜗杆机构在测试固定在沟槽上，可以方便的进行左右移动，右侧立柱可以方便的进行上下移动，保证结构的灵活性。整个装置固定在约500kg的铸铁底座上，保证结构刚性，避免在测试过程中带来不必要的干扰，此外结构由螺栓固定，能够保证连接强度。

（a）管路卡箍结构图                     （b）力方向示意图

图2 管路卡箍结构

FIG. 2 Structure of pipe clamp

图3 金属橡胶与箍带连接形式

FIG. 3 Connection form of metal rubber and hoop belt

（a）线刚度测量装置

（b）角刚度测量装置

图4 刚度测试装置

FIG. 4 Stiffness test device

表2 传感器参数

Table 2 Sensor parameters

3.2 基于力－变形关系的金属橡胶卡箍刚度测定

对金属橡胶卡箍线刚度通过力与变形的关系求出，由 线刚度定义式（4）和式（5），通过试验测试装置在卡箍各方向施加力载荷，载荷的大小由拉压力传感得出，获得金属橡胶卡箍两个方向上的线刚度。

ｘ方向线刚度定义式为：

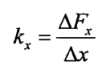                         （4）

ｙ方向线刚度定义式为：

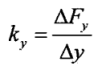                          （5）

式中，、 分别为x、y方向上的加载力变化量，、分别为ｘ、y方向上的位移变化量，卡箍各个方向 的线刚度，可根据力传感器所得的力和千分表所测得的位移变化值，由线刚度定义式（4）和式（5）直接获得卡箍两个方向上的线刚度。

对金属橡胶卡箍角刚度通过扭矩与转角的关系求出，由角刚度定义式（6）和式（7），通过试验测试装置在卡箍各方向施加扭矩，扭矩的大小由扭矩传感测出，卡箍的转角通过角度传感器获得，由角刚度定义式（6）和式（7）直接获得卡箍两个方向上的角刚度。

绕x方向扭转刚度定义式为：

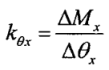                         （6）

绕y方向扭转刚度定义式为：

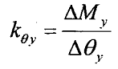                        （7）

式中，、分别为绕ｘ、ｙ方向上的扭矩的变化量，、分别为绕ｘ、y方向上的角位移的变化量。 由角刚度定义式（6）和式（7），可以直接获得卡箍两个方向上的角刚度。

4 管路结构随机振动应力优化分析

对于航空发动机外部管路，位于燃烧室至尾喷口位置 主要受宽频段的随机激励作用，此时在优化设计时应该以 降低振动应力为目标。

4.1 随机振动传递形式

管路的随机振动是通过卡箍及固定端传输到管路本体 上，激振的主要形式如图5所示。应通过分析计算获得卡 箍最合适布局，使管路的振动应力最小，过多的卡箍与过少 的卡箍均不合适，在实际的布局中可以参照《ＧＪＢ3054-97》 进行布置，但是标准并不能十分准确的指导各类情况，通过 仿真分析得到的结果，更具有准确性，对实际的生产指导， 有着更重要的意义。

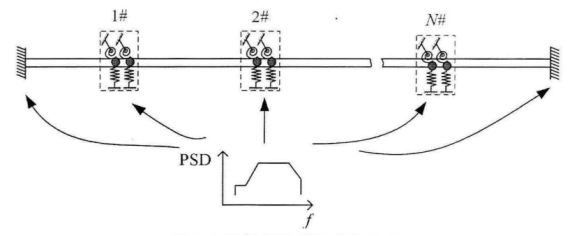
图5 随机振动激励施加位置

FIG. 5 Location of random vibration excitation

4.2 随机振动应力最小优化

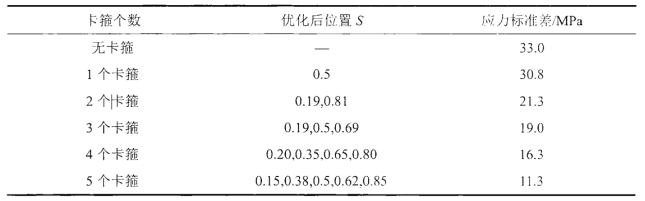
通过计算获得不同数量卡箍时，管路最小振动应力时 的卡箍位置，其中采用ANSYS一阶优化算法进行计算，随机振动的传递形式与上文相同，仿真的计算结果见表3所示， 其中最大应力标准差表示，随机振动应力有68.3％可能性不超过此计算数值，当计算出的随机应力的标准差乘以３倍获得的数值，表示随机振动应力有99.7％可能性不超过此计算数值，本文图表中所列的结果均为１倍的随机振动应力标准差，在本文尺寸下，其中管路随着卡箍数量的增加，管路的应力逐渐减小，管路的随机振动应力从33.0MPa减小为11.3MPa，减小的幅值十分明显，可以看出，在一定程度上增加卡箍的数量，会明显的减小随机振动的应力。

从上文分析可知，卡箍数量及位置对管路的基频及随 机振动应力都有十分显著的影响，在真实管路布局过程中， 应着重考虑这两种边界条件带来的影响。

表3 最大随机振动标准差

Table 3 Standard deviation of maximum random vibration

5 结束语

本文虽然通过有限元软件ANSYS做出了一系列的研究工作，取得了一定的研究成果，但由于作者水平和研究时间等方面的限制，因此本文还存在着很多不足。结合国内外研究现状及本文不足，个人认为在以下几个方面可以做进一步研究与完善：

（１）本文通过有限元软件ANSYS，构建了管路的有限元模型，由于通过试验测定，发现管路振动响应的非线性不强，在工程计算领域，可将管路结构简化为线性模型，但为深层次的掲示管路的振动机理，需要进一步分析卡箍的支承刚度非线性以及卡箍金属橡胶的材料非线性等。

（２）在振动响应的分析计算中，大部分管路振动响应均有试验作为验证，证明了仿真模型及分析方法的有效性， 但在随机振动方面，由于时间及试验条件的限制，未通过试验的手段对仿真进行验证，但仿真分析方法已通过相关书 籍例子进行验证，在进一步的完善中可以通过试验的方法进行验证。

（３）本文管路模型为直线管段或弯管段模型，在管路基本结构的仿真及试验分析中，具有简单易操作的特点，但为更贴近于航空发动机的外部管路，应进一步加强曲管和空间管路的分析计算。

参考文献

[1]杨飞益．复杂空间管路系统动力特性分析与实验验证［Ｄ］．南京：南京航空航天大学，2012．

[2]徐鉴，杨前彪. 输液管模型及其非线性动力学近期研究进展［Ｊ］．力学进展，2004（２）：182－194.

[3]刘海年，刘志强，张大义，等．航空发动机成品振动环境分析与试验载荷谱确定［Ｊ］．航空维修与工程，2013（４）：63－65.

[4]王桂华，刘海年，张大义，等．航空发动机成附件振动环境试验剖面确定方法研究［Ｊ］．推进技术，2013，34（８）：1101－1107.

[5]许锷俊．航空发动机导管结构完整性要求的初步研究［Ｊ］．航空发动机，1994，20（３）：53－62．

[6]GAO PX,YUT,ZHANG YL,et al. Vibration analysisand control technologies of hydraulic pipeline system inaircraft: A review[]]. Chinese Journal of Aeronautics, 2021，34(4):83-114.

[7]刘中华，李兴泉，贾铎，等．航空发动机液压管路裂纹故障分析［Ｊ］．航空发动机，2020，46（５）：66－70．

[8]李洋，佟文伟，韩振宇，等．发动机引气管卡箍断裂原因分析［Ｊ］．失效分析与预防，2013，8（３）：167－172.

[9]刘天文，李舜酩，庞燕龙，等．航空发动机燃油总管支架断裂故障分析［Ｊ］．燃气涡轮试验与研究，2015，28（４）：23－26，56．

[10]刘中华，贾铎，刘鑫．某航空发动机卡箍断裂故障分析［Ｊ］．航空发动机，2019，45（３）：77－81.

[11]尹泽勇，陈亚农．卡箍刚度的有限元计算与实验测定［Ｊ］．航空动力学报， 1999，14（２）：179－182．

[12]沈惠杰，温激鸿，郁殿龙，等．基于Timoshenk梁模型的周期充液管路弯曲振动带隙特性和传输特性［Ｊ］．物理学报，2009，58（12）：8357－8363．

[13]张立翔，杨柯．流体结构互动理论及其应用［Ｍ］．北京：科学出版社，2004： 0－1．

[14]张立翔，黄文虎．输流管路非线性流固耦合振动的数学建模［Ｊ］．水动力 学研究与进展（Ａ辑），2000（01）：116－128.

[15]焦宗夏．传输管路流固耦合振动的模态分析［Ｊ］．航空学报，1999， 20（４）：316－320.

[16]郭猛．高速高压液压管路流固耦合振动14－方程摩擦项修正［Ｄ］．秦皇岛： 燕山大学，2018．

基金项目：四川省自然科学中国民用航空飞行学院学生科学研究基金科技项目“航空发动机管路动力学特性研究”（XSB2023-048）